双层无线传感器网络的中继器放置问题

(杭州电子科技大学理学院，浙江 杭州310018)

0 引 言

在无线传感网络中，如果传感器在传输半径范围内只能将信息传递给高能的中继器，而中继器与中继器之间在传输半径范围内可以相互传递信息，这样的网络称为双层无线传感网络。文献1 首先对无线传感网络2-覆盖2-连通进行了研究，在R≥2r的条件下，给出了性能比为O(Dlogn)的贪婪算法，其中D为网络的直径，n为传感器的数目。文献2 假设传感器集分布在矩形区域内，在R≥4r的条件下给出了两个单覆盖单连通的算法性能比分别为8和6，两个双覆盖双连通的算法，性能比均为9/，而文献3则在三维空间中对该问题进行了讨论。文献4 在R=r的假设前提下针对2-覆盖2-连通问题设计了性能比为24+ε和6/T+12+ε的两种近似算法，其中T为单覆盖单连通问题中放置的中继器数目与网络中传感器数目的比值。本文在双层无线传感网络中加入基站，且在R≥4r的情况下，针对k-覆盖k-连通问题设计了性能比为9/2的近似算法，并给出性能比分析。

1 问题描述与定义

在双层无线传感网络中，中继器可以在传输半径范围内与基站和其他中继器相互传递信息，基站与基站可以直接传递信息。设传感器的集合为X，基站的集合为B，Y表示放置的高能中继器集合，基站的通讯能力是无穷的。

这里假设R≥4r，对给定的(r，R，B，X，Y)，设中继器的传输半径为R，传感器的传输半径为r，给出双层无线传感网络上的混合通讯图MTC(r，R，B，X，Y)的构造方法，其中顶点集V =BUXUY，边集E 定义如下:

(1)对任意顶点bi，bj∈B，E 包含无向边(bi，bj);

(2)对任意顶点y∈Y，z∈Y∪B，如果d (y，z)≤R，则E 包含无向边(y，z);

(3)对任意顶点x∈X，z∈Y∪B，如果d (x，z)≤R，则E 包含无向边(x，z)。

本文研究双层无线传感网络的k-覆盖k-连通放置问题，即放置最小数目的中继器，使得在MTC(r，R，B，X，Y)网络中满足以下两个条件:

(1)每个传感器至少被k个中继器覆盖，即每个传感器至少与k个中继器相连;

(2)中继器与基站构成的网络达到k-连通。

2 算法设计与分析(ω=2)

定义1 如果存在两个传感器s和s'，使得d(s，p)=d(s'，p)=r，则把位置p 称作放置中继器的Pposition[2]。

算法的大体思想是这样的，根据文献5的思想，把传感器和基站所在的区域划分成若干个2r×ω的区域，这里所说的满足特定的条件指的是划分的每个区域至少有一个传感器，ω为算法分区因子，且为正整数，以ω=2为例来设计算法，把每个区域叫做分子。在介绍算法之前，先介绍一个概念。

在寻找所有放置中继器的P-positions时，不一定所找到的P-positions 都在分子内，给定一个分子Ti，P为所有P-positions的集合，对所有p∈P，如果p 不在Ti内，用一个边界上的点q 代替p，点q是Ti到p的最近的距离上的点，这样的操作称为收缩操作[2]。通过收缩操作，可以保证新的P-positions 都在区域内，且同样能覆盖Ti中对应的传感器集。

算法1 k-覆盖k-连通

步骤1 把X∪B 划分成边长为4r的正方形分子，对每个分子，找到所有可以放置中继器的P-positions，并将其收缩到区域内。

步骤2 在每个分子内，搜索X 中所有的放置中继器的P-positions的12k-3个子集，找最小的至少能覆盖分子内每个传感器k次的子集。

步骤3 对每个分子Ti，每个分子内至少包含k个中继器，如果Ti内的中继器不连通，则在距离A为4r的J，K 两处放入两个中继器，在以A为圆心，4r为半径，J，K为端点的圆弧上依次均匀的放入中继器，当k 较大时，可以在以B为圆心，4r为半径，K，M为端点的圆弧上依次的放入中继器，使网络达到k-连通。

步骤4 使得距离较近的中继器达到k-连通。

(1)使中继器集Hi达到行k-连通，设Hi+1为Hi的右边的中继器集合，如果Hi+1和Hi不连通，则在Ti的J 处加入一个新的中继器qi，Hi=Hi∪qi，如果Hi和Hi+1还是不连通，则在Ti+1的J 处(与A点距离为4r)放置一个新的中继器qi+1，Hi+1=Hi+1∪qi+1;如果Hi和Hi+1没有2 连通，则在Ti的K 处放置一个新的中继器qi+2，Hi+1=Hi+1∪qi+2，如果Hi和Hi+1没有2 连通，则在Ti+1的K 处放置一个新的中继器qi+3，则Hi+1=Hi+1∪qi+3;重复以上步骤，直至所有的覆盖分子的中继器集与基站网络都达到行k-连通;如果中继器没有达到k-连通，则在以A为圆心，4r为半径，J，K为端点的圆弧上依次均匀的放入中继器，以B为圆心，4r为半径，K，M为端点的圆弧上依次均匀的放入中继器，直到所有的中继器都达到行k-连通。

(2)使中继器集Hi与基站网络都达到列k-连通。对每个分子Hi，LeftTi={q⊆Hi|q与覆盖Ti左面相邻分子的中继器连通}，RightTi={q ⊆Hi|q与覆盖Ti右面相邻分子的中中继器连通}，如果则有H'i=Hi，否则H'i=Hi-LeftTi∪RightTi。

如果H'i+y和H'i与不连通，则在Ti的J 处放置一个新的中继器qi，Hi=Hi∪qi，接下来的步骤和为使中继器达到行连通类似进行。放置的规则如图1所示:

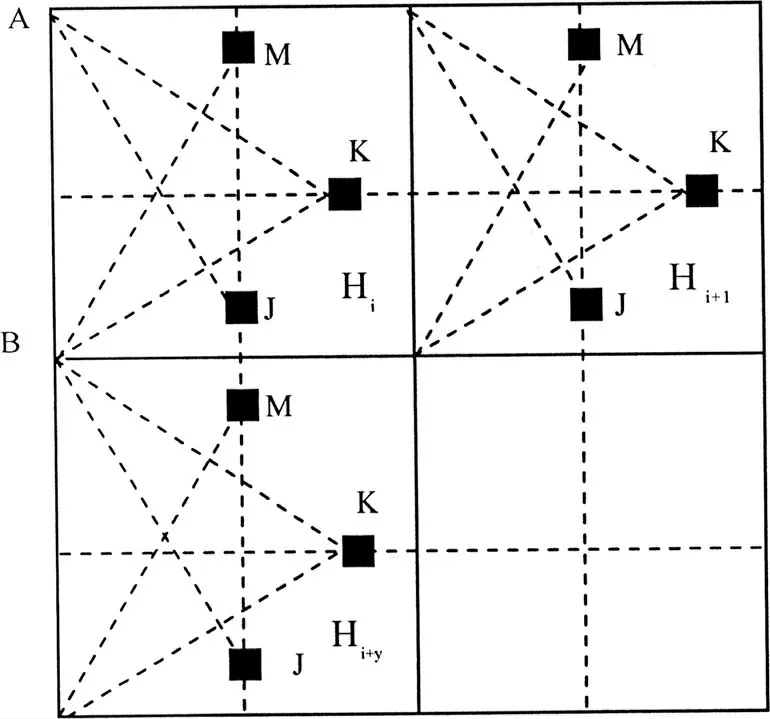
图1 区域划分图

首先可以由该算法的步骤2和4，得到算法1的时间复杂度为O (kn2)。

定理1算法1 在ω=2 下给出问题k-覆盖k-连通的一个解，且算法性能比为9/2。

证明 首先证明该算法得到的中继器集是k-覆盖k-连通的，由步骤1、2可以知道每个分子内的传感器至少被k个中继器覆盖，下面说明中继器集是k-连通的。

(1)每个分子内的任意两个中继器是k-连通的。由步骤2，每个分子内至少有k个中继器，由步骤3，显然每个分子内的任意两个中继器都是k-连通的。

(2)任意两个不在同一个分子内的中继器q，q'。假设q 在分子Ti中，q'在分子Ti+1中，为方便起见，设点q点在第i行第j列，q'在第i'行第j'列，假设i ＜i'，j ＜j'，并且假设Ti中存在同一个中继器与Ti右边及下面的分子内的中继器连通，则Ti中一定存在另外k-1 不相同的中继器与其左边的分子内的中继器连通，否则有LeftTi∪RightTi=k-1，于是q可以通过左右两面k条不同的路径达到q'点。

算法常数性能比为9/2的证明。设Ho为算法1 得到的最优解，H'表示步骤1、2 产生的中继器集合，即H' =∪Hi，设OPT为该问题k-覆盖的最优解，根据Shifting 定理[5]有假定每个分子至少有一个传感器，则H'至少包含k个中继器，根据算法，每个分子至多额外加入k个中继器，因此有所以

通过算法1 性能比的分析，发现运用区域划分思想放置中继器的算法的性能比能达到一个很好的界，当ω=2时k-覆盖k-连通的上界为9/2，随着k值的增大，性能比处于一个恒定的值，不发生变化。对不同的k值使用该算法，发现不管k值如何变化，所得到的问题的算法的性能比均为常数9/2。

3 结束语

本文针对算法分区因子ω=2 设计k-覆盖k-连通问题的算法，证明了算法的性能比为9/2，时间复杂度为O (kn2)，本文只引用了算法分区因子等于2时的情况，是因为随着该值的增大，相应的算法的时间复杂度也会提高。本文运用区域划分的思想，将双层无线传感网络的中继器放置问题提高到了k-覆盖k-连通，拓宽了无线传感网络问题的研究领域。

[1]Hao B，Tang J，Xue G.Fault-tolerant relay node placement in wireless senor networks:Forrmulation and approximation[C].Michigan State:IEEE Workshop on High Performance Switching and Routing，2004:246-250.

[2]Tang J，Hao B，Sen A.Relay node placement in large scale wireless networks[J].Computer Communications，2006，29(7):490-501.

[3]崔素辉.无线传感器网络若干中继器放置问题[D].杭州:杭州电子科技大学，2009:30-35.

[4]Liu H，Wan P，Jia X.On Optimal Placement of Relay Nodes for Reliable Connectivity in Wireless Sensor Networks[J].Journal of Combinatorial Optimization，2006，11(2):249-260.

[5]Hochbaum D S，Maass W.Approximation schemes for covering and packing problems in image processing and VLSI[J].Journal of the ACM，1985，32(1):130-136.