基于单通道接收机的鲁棒自适应波束形成算法

金 伟，贾维敏，张峰干，姚敏立

（1.第二炮兵工程大学，陕西 西安 710025；2.解放军96265部队，河南 南阳 473139）

0 引言

自适应波束形成可以增强期望信号，并对噪声和干扰信号进行有效抑制，已被广泛应用于雷达、声纳、射电天文、地震学、通信和医疗成像等领域［1］。然而，当阵列导向矢量和接收数据协方差矩阵存在失配误差时，自适应波束形成器性能恶化，因此，如何增强自适应波束形成器的鲁棒性一直是学者们研究的一个热点问题［2］。

针对Capon波束形成器这一典型的自适应波束形成器［3］，目前提出了许多种鲁棒波束形成算法。在传统方法中，较具代表性的是对角加载算法［4］和特征子空间法［5］，但前者存在加载量难以选取的问题，而后者在信噪比较低和信号加干扰维数较高时性能受到限制。近年来，基于不确定集理论发展起来的鲁棒自适应波束形成算法，具有清晰的理论架构，是目前公认的较为有效的鲁棒算法，其典型代表为最差性能最优法（Worst－Case，WC）［6］和鲁棒 Capon波束法（Robust Capon Beamformer，RCB）［7］。该类方法通过对导向矢量的失配误差进行建模，将其限定在球体或椭球体内，从而将问题转化为凸优化问题或对最优加载量的数值求解问题，后续许多算法都是对这类算法的改进和再创新［8－9］。另外，由于大多数鲁棒波束形成算法不能对波束形成器主瓣进行精确控制，文献［10—11］提出了可以自由控制主瓣鲁棒响应区宽度和纹波水平的鲁棒波束形成器，文献［12］将之推广至宽带鲁棒波束形成。

然而，上述鲁棒波束形成方法基本上都是基于多通道阵列接收系统进行设计的，它们都需要知道接收数据协方差阵，才可以对问题进行建模求解。为得到接收数据协方差阵，每一个阵元对应接收机的一个通道，即一个阵元接一个接收机，随着阵元数的增加，接收机数量也要增加，因此阵元一多，造价就会很昂贵［13－17］。为减小硬件规模，降低系统成本，基于单通道接收机的阵列信号处理方法近年来得到发展，但其大多用于 DOA 估计［14－17］和无约束的波束形成［13］，并未用于带有约束处理的鲁棒波束形成。

针对以上问题，本文提出了基于单通道接收机的最差性能最优鲁棒Capon波束形成算法。

1 问题描述

对一个具有M个阵元的线性阵列，其输出通常可表示为：

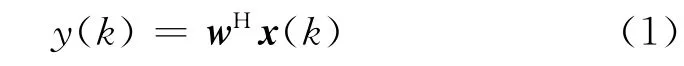
式（1）中，w ＝ ［w1，w2，…，wM］T为自适应阵列加权矢量，y（k）为阵列输出，k代表采样时刻，（·）T和（·）H分别表示转置和共轭转置运算，x（k）为M×1维接收数据矢量，可表示为：

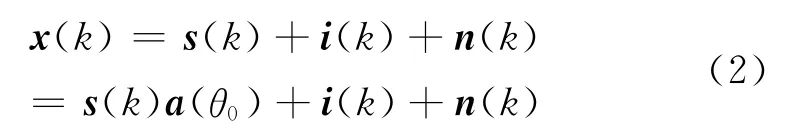
式（2）中，s（k），i（k），n（k）分别为期望信号、干扰信号和高斯白噪声分量，s（k）为期望信号波形，θ0为期望信号方向，a（θ0）为期望信号对应的导向矢量。

1.1 最小方差无失真响应波束形成器

最小方差无失真响应波束形成器是一种典型的自适应波束形成器，通常可表示为［3］：

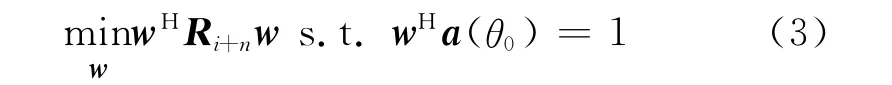
由于这一式子的最优解最早是由Capon求出的，因此又称为Capon波束形成器。式（3）中，Ri＋n表示干扰加噪声协方差矩阵，由于在实际中难以得到，一般都用阵列输出的采样协方差矩阵代替，取采样快拍数为N，则采样协方差矩阵可表示为：

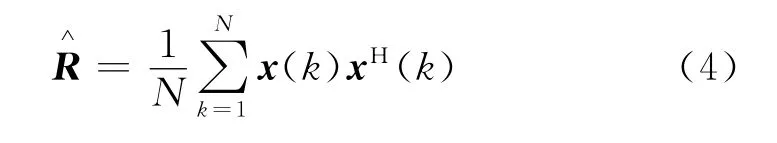
实际中真实的θ0难以精确获得，常用假定值θ－0代替。由于与θ0之间存在一定的失配误差，导致假设的期望导向矢量与真实值存在失配误差，因此期望信号有可能被当作干扰而抑制掉，且这种情况随着期望信号功率的增加愈加严重，此时Capon波束器的性能严重恶化。

为提高Capon波束形成器的鲁棒性，学者们提出了多种鲁棒波束形成算法。对角加载算法（Loaded Sample Matrix Inversion，LSMI）是一种较为常用的鲁棒波束形成算法，可以描述为［4］：

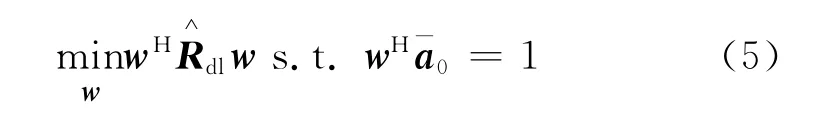
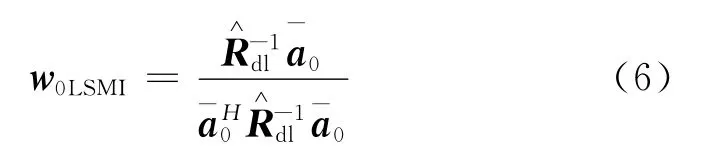
通过引入对角加载矩阵，LSMI算法对噪声子空间的扰动具有一定的抑制能力，从而在一定程度上提高了波束形成器的鲁棒性。该算法的关键问题就是加载因子λ难以选择，其中一个经验取法就是λ等于10倍的噪声功率［4］。但是，这种参数选择方法具有很大的随意性，其效果也有限。许多优秀的不确定集方法都被证明是一种广义对角加载算法，它们之所以效果较好是因为能够找到一个在某种意义上最优的对角加载因子［7］。

1.2 单通道接收机系统

为缩减硬件规模，降低系统成本，削弱通道幅相特性不一致问题对系统性能的影响，学者们提出用单通道接收机来进行阵列信号处理［13－17］。

图1给出了典型的单通道接收机系统示意图［13］。在多通道阵列接收系统中，每个阵元接收的射频信号均由一路通道完成下变频，成为基带信号，而后进行采样合并。单通道接收机系统则不一样，如图1所示，单通道接收机系统在射频阶段进行信号合并，只需要一路接收系统对信号进行下变频。相比于传统的多通道阵列接收系统，单通道接收机系统硬件数量大为减少，系统成本大为降低，同时，也克服了多通道接收系统的通道幅相不一致问题。在单通道接收机系统中，可以进行测量的信息仅为阵列的输出功率，每个阵元接收的基带信号却难以获得以形成接收数据协方差矩阵，因此需要先对协方差矩阵进行估计。

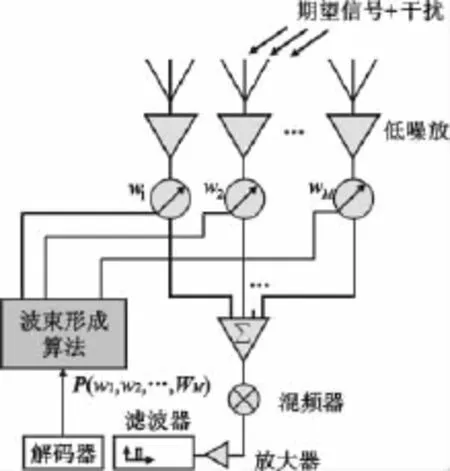
图1 单通道接收机Fig.1 Single－channel receiver

2 基于单通道接收机的最差性能最优鲁棒波束形成

提出的RCB－SPR算法可分为两步：首先对单通道接收机的输出功率运用权微扰算法估计出接收数据协方差矩阵，然后将问题转化为最差性能最优的鲁棒Capon波束形成，从而对真实导向矢量进行估计。

2.1 协方差矩阵估计

采用权微扰算法［14－15］对协方差矩阵进行估计。对平稳随机信号来说，集合平均和时间平均等效，假设接收机接收的信号为平稳随机信号，则有：

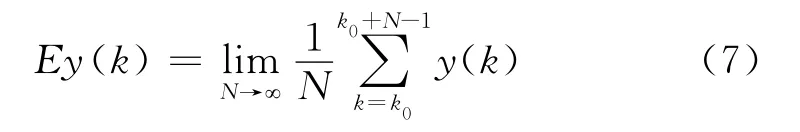
对输出功率来说，则有：

对权矢量进行微小扰动，取w＋＝w0＋Δw和w－＝w0－Δw，式中Δw为权w0附近的微扰，利用两次扰动后的阵列输出功率，可得

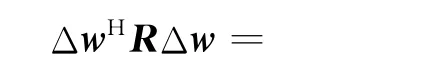
不失一般性，取矩阵R为赫米特阵，即R＝Rr＋iRj，式（9）中Rr是对称的（Ri＝），Rj为反对称的（Rj＝－）。给定Δw＝Δwr＋iΔwj，则有：

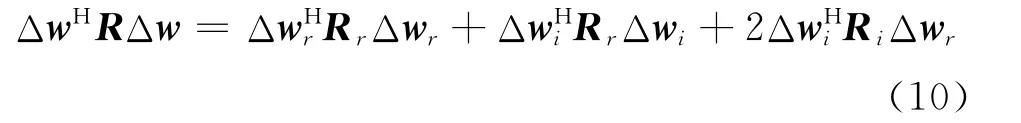
适当选择Δw、R的各元素可以通过接收机的输出y（t）估计得到［15］，即

1）置Δwr＝ei（ei＝ ［0…1…0］T，1在位置i上）和Δwi＝0，则Rr的第i个对角线元素等于ΔwHRΔw；

2）置Δwr＝ei＋ej和Δwi＝0，Rr的元素（i，j），j＞i，可由［ΔwHRΔw－Rr（i，i）－Rr（j，j）］／2求得；

3）Rr剩下的元素可通过对称性求得；

4）由于反对称性，Ri的对角线上元素等于零；

5）置Δwr＝ej和Δwi＝ei，Ri的元素（i，j），j＞i，可由［ΔwHRΔw－Rr（i，i）－Rr（j，j）］／2求得；

6）Ri剩下的元素可通过反对称性求得。

如此，我们就可以对阵列输出的协方差矩阵进行估计。

2.2 最差性能最优的鲁棒波束形成算法

在实际中，由于快拍数量有所限制，再加上由权微扰算法估计协方差矩阵过程中引入的误差，最终估计的协方差矩阵与真实值R之间存在一定的失配误差。因此，我们可将式（3）的Capon波束器转化为：

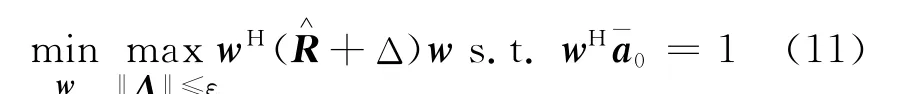
式（11）的优化问题可转化为：

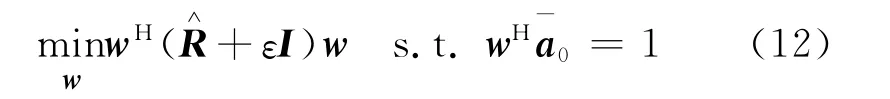
此时，式（12）的最优解为：

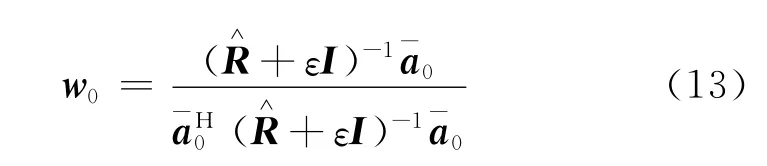
同文献［7］一样，可以将式（12）的优化问题进行转化，令其目标函数为期望信号功率最大化（即令式（14）分母最小化）。同时，为了有效克服导向矢量失配误差对自适应波束形成器的影响，可以将导向矢量约束在一个以假定值为中心的不确定球集内（其半径为γ）。这样，问题可以描述为：

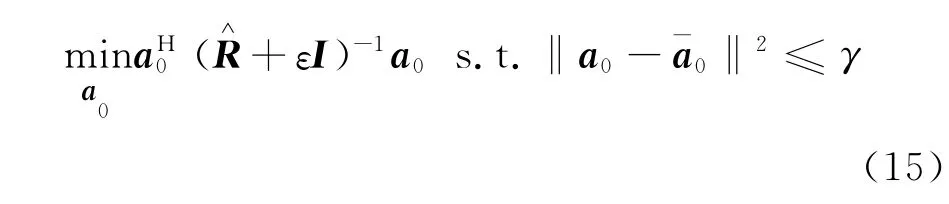
如此，可以采用凸优化工具箱，或者类似于文献［7］采用的数值解方法对式（15）进行求解，从而对真实的导向矢量进行估计。

需要说明的是：1）经权微扰算法估计出协方差矩阵，再经本文的最差性能最优式（11）处理后，也可适用于其他鲁棒波束形成算法，如文献［6］的算法，在此不再赘述；2）仅看式（12）可以发现，它与式（5）的对角加载LSMI算法具有相同的形式。这表明最差性能最优的思想本质也就是找到一个在最差性能最优意义下的最优加载因子，这里关于参数ε的选择我们参照文献［11］，取为ε＝0.（1，1）（（1，1）指的是的第一行第一列元素）。如此一来，ε可随信号功率的变化而变化，能够较好地对的失配误差进行有效约束。

3 实验仿真及结果分析

假设阵列为间隔半波长的均匀线阵，阵元数为10，均为全向阵元。加载的噪声为零均值、单位方差的空间高斯白噪声。假设两个干扰信号分别从－40°和60°入射，功率均为30dB。假设期望信号来波方向为3°。实验对对角加载算法LSMI［4］、最差性能最优法（Worst－Case，WC）［6］、鲁棒 Capon法RCB［7］和本文提出的RCB－SPR算法进行比较。除本文RCB－SPR算法外，其他算法均采用多通道接收机采样的数据进行计算。实验采用100个快拍，实验结果来自100次独立的蒙特卡罗实验。WC算法中不确定集大小取为文献［6］推荐的0.3 M，RCB和本文RCB－SPR算法不确定集大小取为4。

3.1 实验1：归一化方向图比较

该实验主要比较几种算法的归一化方向图。实验中期望信号功率为10dB。期望信号真实方向为0°。图2给出了几种算法的归一化方向图。

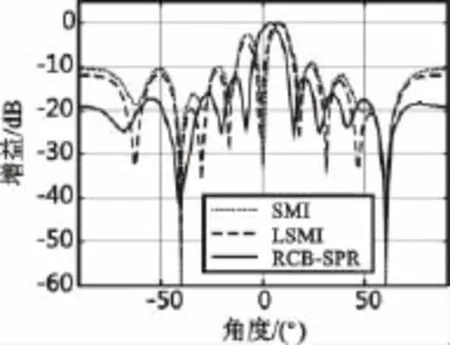
图2 归一化方向图Fig.2 Normalized beampatterns

从图2可知：SMI算法在真实信号方向形成了较深的零陷，这表明SMI算法将真实信号当成干扰进行抑制，实际上期望信号功率越大，这种抑制作用会越明显，因此在真实信号方向形成的零陷就会越深。LSMI算法具有一定的鲁棒性，在真实信号方向形成的零陷不如SMI深，但其鲁棒性并不是特别强。从方向图比较来看，RCB－SPR算法效果较好。

3.2 实验2：期望信号方向失配时不同SNR下的输出SINR比较

该实验主要检验RCB－SPR算法在期望信号存在方向失配时不同输入信噪比（Signal to Noise Ratio，SNR）下的输出信干噪比（Signal to Interference and Noise Ratio，SINR），并与现有方法比较。实验中期望信号真实方向为0°。图3给出了几种算法的输出SINR随输入SNR变化的情况。

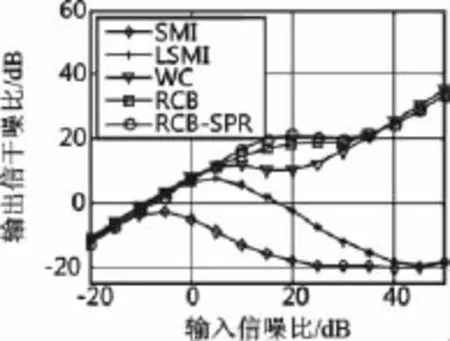
图3 SINR与SNR关系图（存在方向失配）Fig.3 Output SINR versus SNR （no DOA mismatch）

从图3可以看出，SMI算法基本不具备鲁棒性。LSMI算法在低SNR时具备一定的鲁棒性，但随着SNR的增加，LSMI的鲁棒控制能力变得很差，输出SINR明显下降。WC算法、RCB算法和本文的RCB－SPR算法鲁棒性较好，且本文在单通道接收机环境下的RCB－SPR算法与在多通道阵列接收环境下的 WC、RCB算法性能相当，从系统成本角度来看，本文算法优势更为明显。

3.3 实验3：期望信号和干扰同时存在随机方向失配时不同SNR下的输出SINR比较

该实验主要检验期望信号和干扰同时存在随机方向失配时RCB－SPR算法的性能。实验中，期望信号、干扰信号的随机方向失配误差在［－3°，3°］内服从均匀分布。也就是说，期望信号DOA在［0°，6°］内均匀随机分布，两个干扰信号DOA分别在［－43°，－37°］和［57°，63°］内均匀随机分布，但在每次蒙特卡罗实验中，信号DOA均保持恒定。图4给出了该条件下几种算法的输出SINR与输入SNR的关系图。

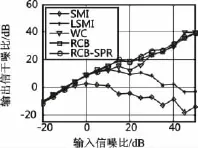
图4 SINR与SNR关系图（随机方向失配）Fig.4 Output SINR versus SNR （random DOA mismatch）

从图中可以看出，SMI算法基本不具备鲁棒性，而LSMI算法的鲁棒性随SNR增加而下降。本文的RCB－SPR算法与WC、RCB算法性能相当，都能较好地克服随机方向失配对自适应波束形成器的影响。

4 结论

本文提出了基于单通道接收机的最差性能最优鲁棒Capon波束形成算法。该算法基于低成本的单通道接收机环境，使用权微扰算法对协方差矩阵进行估计，然后将问题转化为最差性能最优的鲁棒Capon波束形成器。仿真结果表明：提出的算法在单通道接收机条件下，对导向矢量失配误差具有很强的鲁棒性，其性能与基于多通道阵列接收环境下的优秀的不确定集类方法性能相当。提出的算法可以较好地适用于单通道接收机，有效节省系统成本，下一步将继续以单通道接收机为背景，研究信号源DOA移动情况下的鲁棒波束形成问题。

［1］Trees H L Van.Optimum array processing［M］.New York，USA：Wiley Press，2002.

［2］Li J，Stoica P.Robust adaptive beamforming［M］.New Jersey，USA：Wiley，2005.

［3］Capon J.High－resolution frequency－wavenumber spectrum analysis［J］.Proceedings of the IEEE，1969，57（8）：1 408－1 418.

［4］Carlson B D.Covariance matrix estimation errors and diagonal loading in adaptive arrays［J］.IEEE Transactions on Aerospace and Electronic Systems，1988，24（4）：397－401.

［5］Feldman D D，Griffiths L J.A projection approach for robust adaptive beamforming［J］.IEEE Transactions on Signal Processing，1994，42（4）：867－876.

［6］Vorobyov S A，Gershman A B，Luo Z Q.Robust adaptive beamforming using worst－case performance optimization：a solution to the signal mismatch problem［J］.IEEE Transactions on Signal Processing，2003，51（2）：313－324.

［7］Li J，Stoica P，Wang Z S.On robust capon beamforming and diagonal loading［J］.IEEE Transactions on Signal Processing，2003，51（7）：1 702－1 715.

［8］Shahbazpanahi S，Gershman A B，Luo Z Q，et al.Robust adaptive beamforming for general－rank signal models［J］.IEEE Transactions on Signal Processing，2003，51（9）：2 257－2 269.

［9］Jin W，Jia W M，Yao M L，et al.Iterative doubly constrained robust Capon beamformer［J］.Electronics Letters，2011，47（25）：1 372－1 373.

［10］Yu Z L，Ser W，Er M H，et al..Robust adaptive beamformers based on worst－case optimization and constraints on magnitude response［J］.IEEE Transactions on Signal Processing，2009，57（7）：2 615－2 628.

［11］Liao B，Tsui K M，Chan S C.Robust beamforming with magnitude response constraints using iterative secondorder cone programming［J］.IEEE Transactions on Antennas and Propagation，2011，59（9）：3 477－3 482.

［12］陈明建，罗景青.基于幅度响应约束的稳健自适应宽带波束形成［J］.探测与控制学报，2011，33（5）：34－40.CHEN Mingjian，LUO Jingqing.Robust adaptive broadband beamforming based on constraints magnitude response［J］.Journal of Detction and Control，2011，33（5）：34－40.

［13］Fakharzadeh M，Jamali S H，Mousavi P，Safavi－Naeini S.Fast beamforming for mobile satellite receiver phased arrays：theory and experiment［J］.IEEE Transactions on Antennas and Propagation，2009，57（6）：1 645－1 654.

［14］赵益民，鞠德航.协方差矩阵的微扰权算法［J］.电子学报，1996，24（3）：125－127.ZHAO Yimin，JU Dehang.A wight perfurbation algorithm of the covariance matrix［J］.Acta Electronica Sinica 1996，24（3）：125－127.

［15］赵益民，鞠德航.单通道接收机实施空间谱估计测向［J］.通信学报，1997，18（2）：7－11.ZHAO Yimin，JU Dehang.The spatial spectrum estimation direction finding via a single port receiver［J］.Journal of China Institute of Communications，1997，18（2）：7－11.

［16］叶中付，吴涛.用单通道接收机实现方位超分辨的一种方法［J］.信号处理，2001，17（2）：192－194.YE Zhongfu，WU Tao.A method for super－resolution direction finding with single channel receiver［J］.Signal Processing，2001，17（2）：192－194.

［17］张珂，马鹏，张剑云.单通道阵列无失真空时二维谱估计算法［J］.数据采集与处理，2011，26（6）：654－660.ZHANG Ke，MA Peng，ZHANG Jianyun.Distortionless space－time spectrum estimate algorithm in switch antenna array system［J］.Journal of Data Acquisition and Processing，2011，26（6）：654－660.