基于联合子空间的宽带弱信号测向算法

苏成晓，罗景青，樊甫华

（解放军电子工程学院，安徽 合肥 230037）

0 引言

为了实现对目标的实时检测与方向估计，通常雷达前端在待测空域预设波束位置形成多波束，不用扫描就可实现目标信号的来波方向估计［1－2］。而在电子对抗环境中，雷达多波束系统接收到的不仅有有用信号，还有各种各样的干扰［3］，通常干扰的强度远大于有用信号，这会严重影响弱信号的检测与方向估计［4］。因此，研究强干扰环境下宽带多波束系统中弱信号的测向问题具有实际意义。

强干扰与弱信号并存时，尤其是角度间隔相近时，弱信号的谱峰通常被强干扰的谱所淹没。实现强干扰环境下弱信号的方位估计，首先要消除强干扰的影响。文献［5］将多级恒模阵列应用到强干扰存在时弱信号的测向中，该方法对于弱信号的测向是有效的，但是运算量巨大，且分辨性能较差。文献［6］使用阻塞矩阵和正交投影矩阵抑制干扰，算法需要预先估计强干扰方向。文献［7—8］分别针对均匀线阵和均匀圆阵，通过子阵波束形成实现干扰抑制，该算法在大型阵条件下有较好的应用前景。这些方法针对的都是阵元域窄带信号，且强干扰方向估计不准确会对后续弱信号方位估计产生较大影响。为了实现强干扰环境下宽带多波束系统中弱信号的测向，本文提出了一种基于干扰－噪声联合子空间的宽带波束域弱信号超分辨测向算法。

1 信号模型与宽带波束域MUSIC算法

考虑阵元数为L的宽带阵列，阵元在阵列平面中的坐标分别为 （xk，yk），k＝1，2，…，L ，空间形成M 个波束，中心指向分别为 （φ（m），β（m）），m ＝1，2，…，M ，φ（m）为方位角，β（m）为俯仰角。设信号方向分别为 （φi，βi），i＝ 1，2，…，P ，P 为信号总个数。波束形成采用幅度加权和时延控制的方式，记第m号波束的输出为bm（t），m ＝1，2，…，M ，则

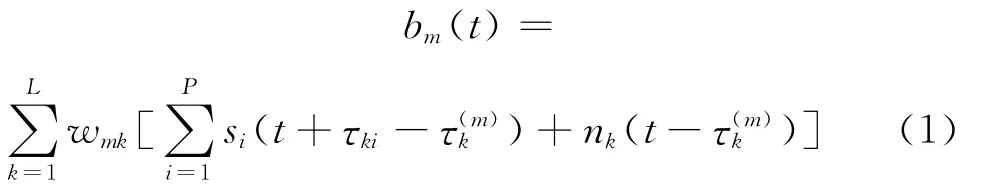
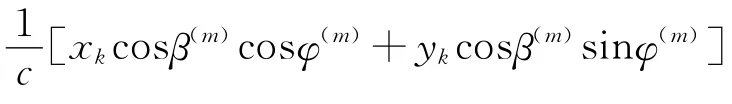
宽带波束域 MUSIC算法［9］，解决的是如何从bm（t）中估计信号的来波方向。对bm（t）傅里叶变换，得到波束域频域数据B（f），然后将带宽划分为Q个子带，对应于中心频率为fq的窄带子带，构造聚焦矩阵T（fq），Q个子带聚焦后的协方差矩阵为

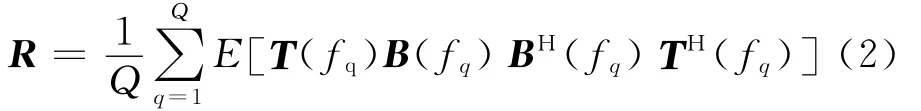
对R特征分解，特征值由大到小分别为λi，i＝1，2，…，M，最小的M－P个特征值对应的特征向量张 成 噪 声 子 空 间 EN＝ ［eP＋1，eP＋2，…，eM］，用MUSIC算法构造空间谱

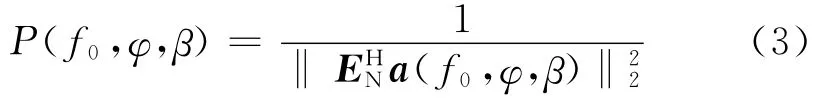
式（3）中a（f0，φ，β）为聚焦频率处的波束域方向向量。式（3）即为宽带波束域 MUSIC算法，记为WMC－MUSIC。强干扰的存在使得宽带波束域MUSIC算法不能正确估计弱信号的来波方向，因此进行弱信号的测向首先要消除强干扰的影响。

2 基于干扰－噪声联合子空间的弱信号方位估计

本文根据子空间理论，定义干扰子空间，并将之与噪声子空间联合构造干扰－噪声联合子空间，用以代替原来的噪声子空间进行空间谱估计，有效地抑制了强干扰的谱峰，实现了弱信号的正确测向。

2.1 干扰子空间定义及构造

对R特征分解后，信号子空间ES和噪声子空间EN可以表示为

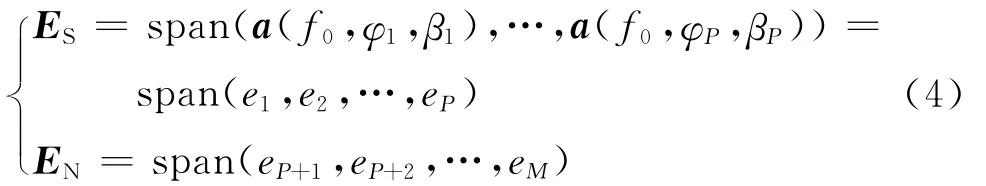
假设有用信号个数为 D，方向记为 （φUi，βUi），i＝1，2，…，D ，干扰个数为J，方向记为 （φJj，βJj），j＝1，2，…，J，其中P＝D＋J。如果干扰与有用信号分开处理，定义干扰对应方向向量张成干扰子空间EJ，有用信号对应方向向量张成有用信号子空间EU。

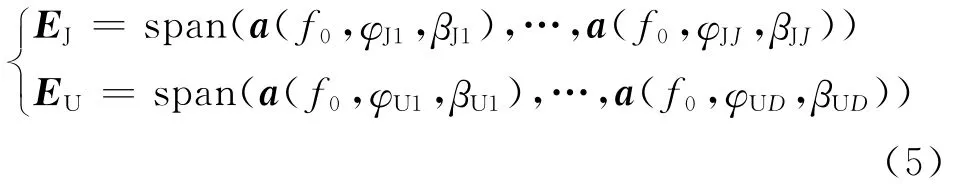
当干扰功率远大于其余所有信号时，协方差矩阵特征分解的前J个大特征值对应的特征向量张成的空间近似为干扰子空间，强干扰功率越强，这种近似程度越高。即当强干扰功率远大于有用信号功率时，可以近似认为

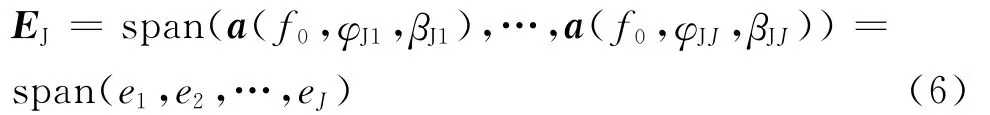
由（6）易知，无需强干扰的方向就可以得到干扰子空间的近似估计。干扰子空间EJ与有用信号子空间EU为总信号子空间ES的子空间，且有ES⊥EN，EJ⊥EN，EU⊥EN，但EU与EJ并不一定正交。

2.2 基于联合子空间的弱信号方位估计

子空间类算法利用信号方向向量与噪声子空间的正交性构造空间谱，某一角度空间谱值为该方向向量向噪声子空间的投影模值平方的倒数。若在噪声子空间中并入某方向向量，进行谱估计时该方向上必不产生峰值点。因此，可以将强干扰对应方向向量并入噪声子空间来抑制干扰方向谱峰的出现，但这需要预先估计强干扰方向，强干扰方向估计不准确则其对应的方向向量也会偏移，使得算法性能下降。根据上节中干扰子空间的定义，可以利用特征分解后强干扰对应特征向量来近似得到干扰子空间，然后将干扰子空间与噪声子空间联合，构造干扰－噪声联合子空间，代替原来的噪声子空间进行估计，这样进行估计时，强干扰的谱峰得到抑制，只会出现弱信号的谱峰。

将干扰子空间EJ＝ ［e1，e2，…，eJ］与噪声子空间EN＝ ［eP＋1，eP＋2，…，eM］联合，构造干扰 －噪声联合子空间

虫害重点防治螟虫、褐飞虱的发生，病害稻瘟病、白叶枯病和稻曲病防治尤为关键，根据病虫情报，适时防治病虫害。

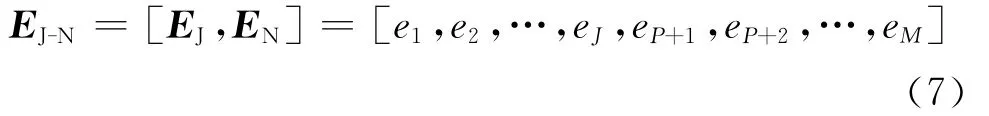
根据方向向量与联合子空间的正交性构造空间谱

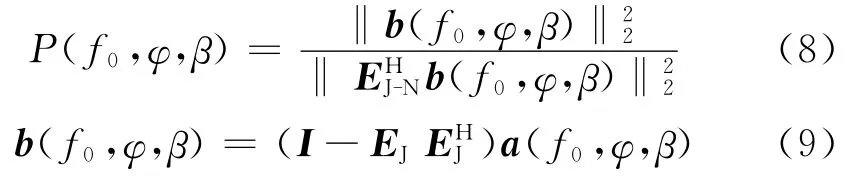
其中b（f0，φ，β）为变换后的波束域方向向量，（IEJ）为干扰正交补子空间的投影矩阵。对波束域方向向量进行变换，是为了保证变换后弱信号对应的方向向量与干扰－噪声联合子空间正交，谱峰搜索时弱信号方向产生峰值。

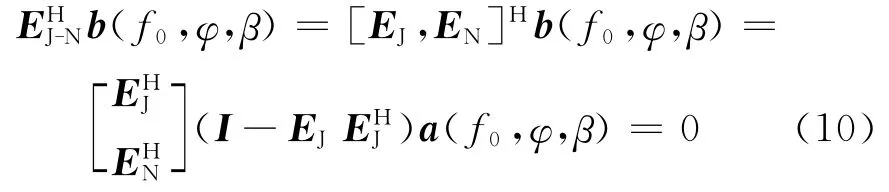
弱信号对应方向向量b（f0，φ，β）与干扰 －噪声联合子空间EJ－N正交，这样进行搜索的时候能保证弱信号的方向形成谱峰。当（φ，β）对应强干扰方向时，b（f0，φ，β）＝0。实际中由于有限次快拍，阵列自身误差的影响，估计得到的干扰－噪声联合子空间与真实子空间存在误差，b（f0，φ，β）就不为零而是一个模值很小的向量，将其模值放在分子上，谱峰搜索时能够避免强干扰方向产生谱峰。

2.3 算法步骤

本文算法步骤可以概括为：

步骤1）对多波束数据FFT后进行聚焦变换；

步骤3）利用式（7）构造干扰－噪声联合子空间；

步骤4）利用式（8）（9），根据方向向量与干扰－噪声联合子空间的正交性构造空间谱。

之前的强弱信号测向算法主要采用预处理方法，首先估计强干扰的方向，然后构造预处理矩阵抑制干扰，最后进行弱信号的测向，强干扰方向估计不准确会对后续处理产生很大影响。而本文算法无需预处理，强干扰抑制与弱信号方位估计同步进行，算法简单，运算量小，且无需预估强干扰方向。

3 仿真实验

实验1：算法空间谱估计结果

考虑16元均匀线阵，空间形成4个波束，波束间－3dB交叠，1—4号波束中心指向分别为－9.6°、－3.2°、3.2°、9.6°，幅度采用－30dB切比雪夫加权。假设多波束系统接收到3个宽带信号，其中两个信噪比（SNR）均为0dB的有用信号，方向分别为－9°、－3°，一个干噪比（INR）为40dB的强干扰，方向为0°。信号与干扰同频段，中频频率为275～475MHz，采样频率512MHz，阵元间距为信号中心频率对应波长的一半，噪声为复高斯白噪声。图1为本文算法与 WMC－MUSIC算法进行100次蒙特卡洛实验谱估计结果。

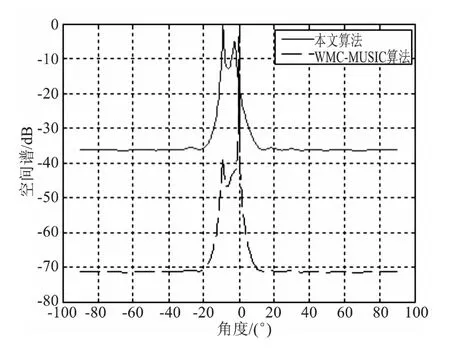
图1 算法空间谱Fig.1 Spatial spectrum

从图1可以看出，WMC－MUSIC算法估计时，－9°方向的弱信号和0°方向的强干扰能够正确分辨，而－3°方向的弱信号，由于受到邻近0°方向强干扰的影响，已经无法分辨。而采用本文算法，0°方向强干扰谱峰得到抑制，－3°方向出现弱信号的谱峰，表明本文算法使用干扰－噪声联合子空间，能够有效抑制强干扰的影响，实现多波束系统中弱信号的正确测向。

实验2：算法估计性能

假定多波束系统接收到两宽带信号，其中一个为信噪比0dB的有用信号，一个为干噪比40dB的干扰。固定弱信号方向为－3°，假定强干扰与弱信号信号间隔为2°：0.5°：10°，即干扰方向为 －1°：0.5°：7°时，观察干扰与信号角度间隔对算法的影响，其他仿真条件同实验1。图2为算法性能与干扰和信号角度间隔关系曲线。

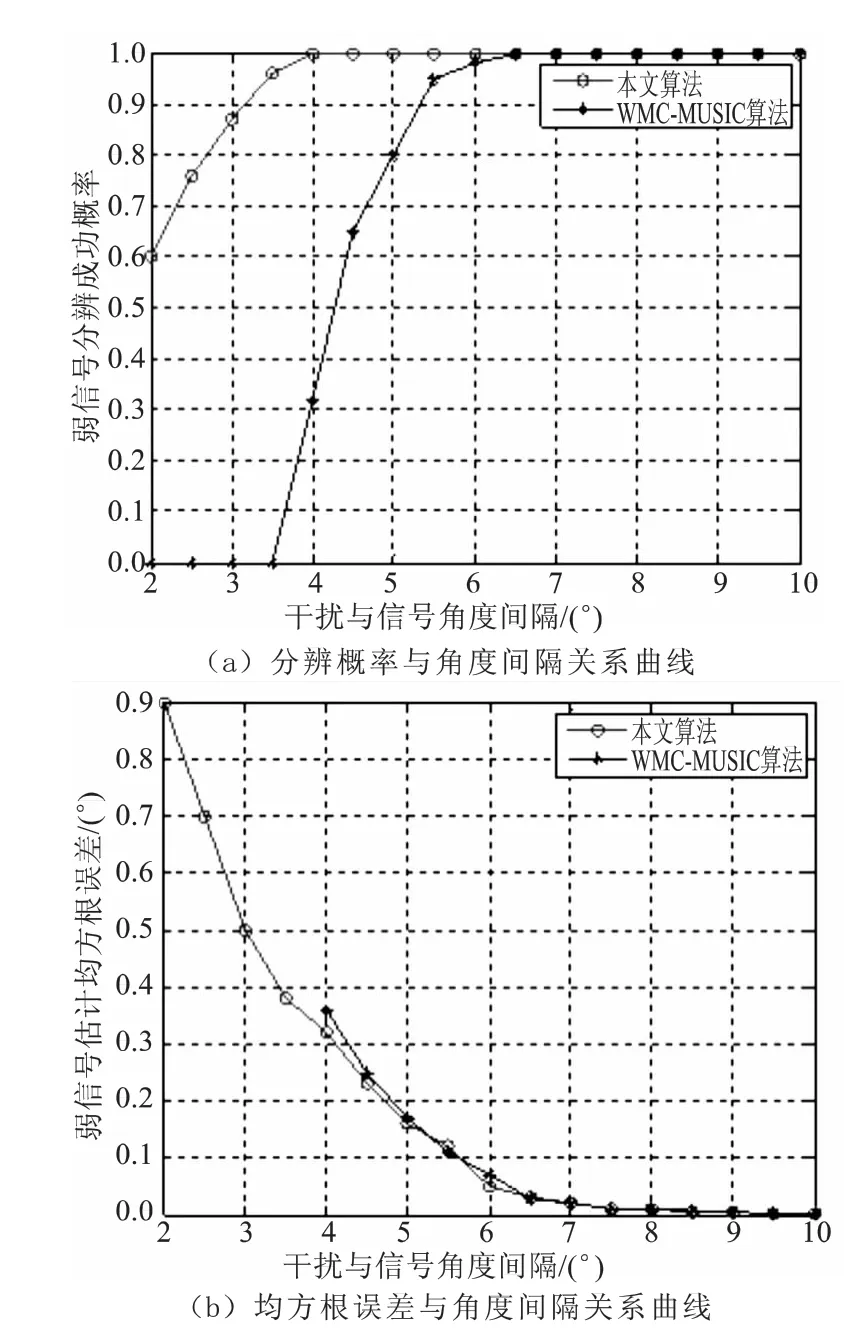
图2 算法性能与角度间隔关系曲线Fig.2 Curve of statistical performance versus jamming－signal spatial interval

图2（a）为弱信号分辨成功概率与角度间隔关系曲线，可以看出，干扰与信号角度间隔越大，算法的分辨概率越高，对于 WMC－MUSIC算法，在给定仿真条件下完全分辨角度间隔至少为6.5°，而本文算法将完全分辨时的角度间隔减小至4°。当角度间隔小于6.5°时，同一角度间隔下本文算法的分辨概率大于 WMC－MUSIC算法，说明本文算法提高了弱信号的分辨和检测概率。

图2（b）为弱信号方位估计均方根误差与角度间隔关系曲线，可以看出，均方根误差随着干扰与信号角度间隔增大而减小。而WMC－MUSIC算法和本文算法均方根误差基本相同，说明本文算法并不能提高弱信号的估计精度，这主要是因为MUSIC类算法对某一信源DOA估计的均方误差仅与该信源信噪比、信源的空间位置以及信源间的相关性有关。

图3为不同干噪比条件下算法性能与信噪比关系曲线。信号方向为－3°，干扰方向为0°，信噪比从－5dB变化到15dB，干噪比分别为15dB、50dB、80dB，其他仿真条件同上。

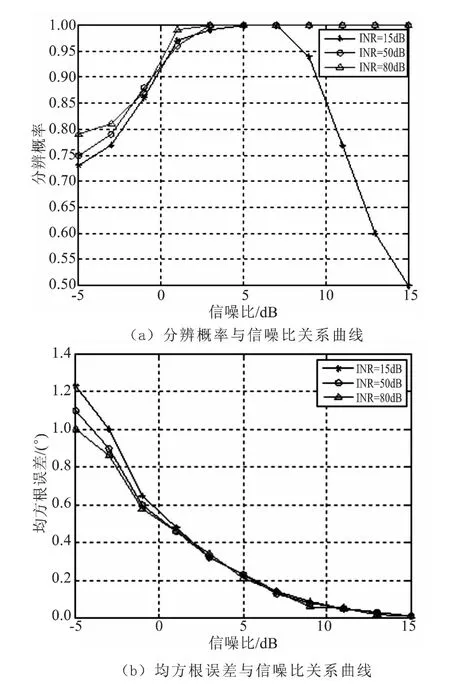
图3 不同干噪比下算法性能与信噪比关系曲线Fig.3 Curve of statistical performance versus SNR under different INR

图3（a）为不同干噪比条件下本文算法分辨概率与信噪比关系曲线。在干噪比为50dB和80dB时，算法分辨概率曲线大致相同，分辨概率随着信噪比增大而增大，这是因为干扰功率远大于信号，通过特征向量近似得到的干扰子空间能够代表真实干扰子空间，此时信号的分辨概率主要取决于信噪比。而当干噪比为15dB，信噪比大于7dB时，分辨概率反而随着信噪比增大而减小，这是因为此时干扰与信号功率接近，估计干扰子空间时有可能将信号方向对应特征向量包含进去，从而使信号分辨概率下降。

图3（b）为不同干噪比条件下均方根误差与信噪比关系曲线。由图可知，在正确分辨的前提下，不同干噪比时曲线大致相同，均方根误差随着信噪比的增大而减小，而与干噪比无关。

4 结论

本文提出了一种强干扰环境下宽带多波束系统弱信号超分辨测向算法。首先对多波束数据FFT后进行聚焦变换，然后估计频域协方差矩阵并特征分解，接着将干扰对应特征向量并入噪声子空间，构造干扰－噪声联合子空间，最后利用方向向量与干扰－噪声联合子空间的正交性构造空间谱，抑制干扰的同时实现了弱信号的正确测向。实验表明，提出的算法能够有效消除强干扰对邻近弱信号的影响，提高了弱信号的分辨概率，同时算法无需估计强干扰方向，运算量小，有利于工程实现。

［1］侯颖妮，黄建国，冯西安.基于多波束系统的波束域方位估计方法研究［J］.弹箭与制导学报，2007，27（3）：80－82.HOU Yingni，HUANG Jianguo，FENG Xi’an.The study on beam－space DOA estimator based on beam－forming system［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（3）：80－82.

［2］龙宁，张凤荔.基于FFT的数字多波束测向算法研究［J］.电子科技大学学报，2005，34（1）：16－18.LONG Ning，ZHANG Fengli.A digital multi－beams algorithm of DOA estimation based on FFT［J］.Journal of UEST of China，2005，34（1）：16－18.

［3］龚耀寰.自适应滤波（第二版）：时域自适应滤波和智能天线［M］.北京：电子工业出版社，2003：99－100.

［4］陈辉，苏海军.强干扰／信号背景下的DOA估计新方法［J］.电子学报，2006，34（3）：530－534.CHEN Hui，SUN Haijun.A new approach to estimate DOA in presence of strong jamming／signal suppression［J］.Acta Electronica Sinica，2006，34（3）：530－534.

［5］潘苗，王鼎，吴瑛.多级恒模在强干扰下弱信号测向中的应用［J］.现代雷达，2008，30（3）：62－66.PAN Miao，WANG Ding，WU Ying.Cascadedconstant modulus for DOA estimation of weak signal under existence of strong jamming ［J］.Modern Radar，2008，30（3）：62－66.

［6］王鼎，张莉，吴瑛.两种强干扰下弱信号的二维波达方向估计算法研究［J］.系统仿真学报，2009，21（10）：2866－2871.WANG Ding，ZHANG Li，WU Ying.Twodirection－ofarrival estimation algorithms research for weak signals in presence of strong interference signals［J］.Journal of System Simulation，2009，21（10）：2866－2871.

［7］柴立功，罗景青.一种强干扰条件下微弱信号DOA估计的新方法［J］.电子与信息学报，2005，27（10）：1 517－1 520.CHAI Ligong，LUO Jingqing.A novel algorithm for weak signals’DOA estimation under intensive interferences［J］.Journal of Electronics ＆Information Technology，2005，27（10）：1 517－1 520.

［8］苏成晓，罗景青.一种均匀圆阵子阵干扰抑制DOA估计算法［J］.信号处理，2010，26（9）：1 355－1 360.SUChengxiao，LUO Jingqing.A novel DOA estimation algorithm via subarray jamming suppression based on uniform circular array［J］.Signal Processing，2010，26（9）：1 355－1 360.

［9］夏斌，闫东，王文博.基于聚焦矩阵的超宽带信号DOA估计［J］.电路与系统学报，2007，12（2）：115－117.XIA Bin，YAN Dong，WANG Wenbo.An estimation method of direction－of－arrival for UWB signal based on focusing matrix［J］.Journal of Circuits and Systems，2007，12（2）：115－117.