社交网络种子节点搜索算法

张 璐，蔡皖东，彭 冬

（1.西安市烟草专卖局，陕西 西安710061；2.西北工业大学 计算机学院，陕西 西安710072）

0 引 言

随着Web2.0技术的发展，社交网络已成为互联网中非常流行的网络应用[1]。目前，一些大规模在线社交网站，如Facebook的访问量已经超过谷歌，成为美国第一大网站[2]。社交网站每天都有数百万在线用户，这包含着巨大潜在的商机，比如一些公司可以利用社交网站在线用户来推销他们的产品。

在社交网络中，种子节点的影响力对推动信息传播是非常重要的。一些通过病毒式市场营销方式来推销其产品、服务的公司或用户对如何选择具有影响力的种子节点怀有很大的兴趣。比如A公司想在社交网站为其产品做广告，由于广告费用有限，只能投放K个用户，A公司希望这些最初的用户能够喜欢其产品，并以他们作为种子节点，在社交网络中以口碑相传方式来影响他们的朋友，让他们的朋友也喜欢其产品，而他们的朋友又通过社交网络进一步影响更多的朋友，使更多的用户都能喜欢其产品。A公司当然希望最初选择的用户 （即种子节点）都具有较大影响力，所影响的人数尽可能地多，从而花费少量的费用就可达到最大的广告效益。可见，种子节点在网络信息传播过程中发挥了重要的作用，他们相当于意见领袖，通过他们的引导和影响，局部意见可能演化为网络舆论。统计数据显示，网络中的大部分用户不经常参与信息的制造与传播，他们做出的决定往往跟随意见领袖。有效地识别网络意见领袖，通过意见领袖发表引导性信息来影响所在网络用户而非直接说服他们，可以有效地触发整个网络或社会的影响力，对于推动信息传播，提高广告效应具有重要的现实意义。

人们从不同角度研究了社交网络意见领袖发现和识别问题，通过搜索社交网络中影响力最大的种子节点来发现和识别意见领袖是其中的一种重要方法，并引起业界的关注和重视，将此类问题归结为影响力最大化问题。

目前，影响力最大化算法主要分为两类:复杂网络算法，比如基于节点度和基于中心的算法等，这类算法存在的主要问题是所得到的种子节点影响力偏低；贪婪算法，其主要问题是计算效率较低、计算时间不稳定以及可扩展性较差等。

为了克服以上算法的不足，本文提出了一个新的启发式贪婪算法，其主要特点是在部分度数高的节点中搜索种子节点并计算影响力，在不损失影响力的情况下，使计算效率有了较大提高。

1 相关工作

近年来，影响力最大化问题得到学者的广泛关注和研究，比较有代表性研究成果如下。

文献[3]提出了一种基于帖子内容分析的博客重要用户分析方法ThreadRank，该方法通过分析大量的博客内容来判断其用户的重要性，需要耗费大量的时间用于内容清理和分析，效率较低。

文献[4]提出一种意见领袖识别方法InfluenceRank，该方法根据与其他博客相比较来判断用户的重要性，以及这些用户对整个网络所做的贡献来计算用户权值，该文采用了余弦定理计算不同博客实体的相似性，复杂性较高，开销大。

文献[5]提出了一种Twitter网络节点计算方法TwitterRank，该方法根据Twitter中的用户关系、粉丝与关注者之间的分布以及在信息传播的过程中各种用户群体所起到的作用进行权重计算，该算法主要基于话题进行分析，召回率不高。

文献[6]研究了如何对社会影响力进行定量分析，通过因子图建模，提出了3种学习算法，但文中用到的LDA和因子图降低了其效率。

文献[7]根据社交网络节点之间的交互信息和拓扑信息，利用线性回归模型预测节点之间的影响力大小，结果表明交互信息其主导作用，拓扑信息作用较小。该方法仅利用了Facebook上的数据，结论是否适合于其他社交网络待进一步验证。

文献[8]以Twitter为实验对象，比较了基于粉丝数排序、基于微博转发数排序和基于PageRank排序等3种影响力排序方法以及不同排序方法之间的相关性。

文献[9]基于用户发表话题的关注程度，对影响力进行度量和排序，但没有与其它影响力排序方法进行比较。

文献[10，11]从不同的角度，对PageRank方法进行扩展和改进，对用户影响力进行度量和计算。但没有从根本上克服PageRank方法自身的缺陷。

文献[12]提出一个基于子模函数理论的优化贪婪算法 （cost－effective lazy forward selection，CELF），算法在部分影响力较大节点中搜索种子节点，由于搜索空间的减少，算法效率有了较大提高。实验结果显示，CELF算法得到的种子节点影响力与原始贪婪算法相同，而计算速度提高了近700倍，但对于大规模社交网络，它的计算效率依然比较低。

文献[13]提出一个新的贪婪算法 （new greedy），基本思想是在社交网络图中，以节点间影响因子p选择相关边，建立一个全新的子图，然后选择子图中度数最大的节点作为种子节点，并且还提出一个MixGreedy算法，它分为两部分:第一部分采用NewGreedy算法思想选取第一个种子节点；第二部分采用CELF算法思想选取余下种子节点。MixGreedy算法结合了NewGreedy算法和CELF算法的优点，其计算效率比CELF算法有所提高。由于在线性阈值模型中节点间并不以影响因子p来相互激活，MixGreedy算法需要从独立级联模型或带权级联模型中求得种子节点，再在线性阈值模型中计算它们的影响力，因此其影响力大小与其他贪婪算法有时相差较大，在线性阈值模型中可扩展性较差。

2 种子节点搜索算法

下面首先介绍经典贪婪算法，然后给出本文提出的算法。

在描述算法之前，定义σ（·）为影响力函数，S为种子节点集合，U为搜索节点集合。σ（S）是种子节点集合S的影响力，即集合S影响节点数目大小。

基于优化贪婪算法的种子搜索算法

定义1 如果对于任何元素x，y∈RK有f（x∨y）＋f（x∧y）≤f（x）＋f（y），则函数f:Rk→R是子模函数。

由定义1可以得出如下结论。

结论1:如果f是子模函数，则ABN，j∈N＼B，有f（A＋j）－f（A）≥f（B＋j）－f（B）。

由此可见，任何子模函数具有单调、非负等性质。

结论2:在独立级联模型、带权级联模型和线性阈值模型的任何一个实例中，影响力函数σ（·）是一个子模函数。

由结论2可知，随着集合S的节点数目增多，集合U中所有节点的影响力都在逐渐减弱，具有单调递减性。

为此，文献[12]基于影响力具有子模函数的性质提出了CELF优化贪婪算法，它可分为两个步骤:在第一个步骤中，算法计算所有节点影响力，选择影响力最大的节点作为第一个种子节点加入到种子节点集合中；在第二个步骤中，算法选择余下的种子节点，在每次选择种子节点过程中，基于影响力具有子模函数性质的算法只计算部分影响力大的节点。

下面给出CELF算法的伪代码:

基于启发式贪婪算法的种子节点搜索算法

相比于原始贪婪算法，CELF算法的计算效率有了较大提高，但是在大规模社交网络中搜索种子节点依然非常耗时。本节将首先分析社交网络特征，然后给出改进算法。

为了使实验条件相同，本文使用的数据集与文献[13，14]中所用的数据集相同，均来源于论文共享网站arxiv（www.arxiv.org），其中网络中的节点代表学者，边代表学者间科研合作关系，而科研合作关系主要体现在论文合作方面。第一个科研合作网来自于 “高能物理理论”版块，从1991年至2003年，用NetHEPT表示，它包含15233个节点和58891条边。第二个科研合作网来自于 “物理学”版块，用NetPHY表示，它包含37154个节点和231584条边，本文将对此数据集进行分析，包括节点的度分布以及节点的度与影响力的关联性。

对于节点的度与影响力的关联性，上述两种网络选择在独立级联模型中计算所有节点的影响力，分析度与影响力的关联性，图1给出了节点的度与影响力散点图，其中横坐标表示节点度大小，纵坐标表示节点的影响力均值。

图1 独立级联模型中节点的度与影响力散点

由图1可见，节点度数越高，影响力也就越大，但是在度数较大节点中影响力均值偏差较大，原因是由于度数较大节点数量少，个别节点的影响力对均值影响较大。比如在NetPHY中所有度数大于150的节点只有157个，其平均在每个节点度的分布约为2.5个，所以节点的度数与影响力存在着较强的关联性。这也符合实际的社交网络，比如在人际关系网中用户的朋友关系越多，那么受他影响的人数一般也就越多，其深层次的原因是在社交网络中边是信息传播的唯一路径，度数高的节点连接着大量的边，因而其影响的范围相对也就较大。

节点的度呈幂律分布以及节点的度与影响力强关联性说明，社交网络存在着大量影响力较小的节点和少量影响力较大的节点，而在影响力最大化问题中种子节点具有较大影响力，大量影响力较小的节点，即度数低的节点，成为种子节点的概率非常低，可以考虑将它们排除在种子节点搜索范围之外，从而缩小种子节点搜索的范围。

基于以上分析，本文提出了一种新的启发式贪婪算法－高节点度贪婪算法 （HD＿Greedy），算法描述如下:

该算法考虑了节点度数大小，其基本思想是在极小部分高度数节点中搜索种子节点，其过程分为两个步骤:在第一个步骤中，算法首先输入高度数节点占所有节点的百分比r，0＜r≤1，对所有节点按度数由大到小排序，选择排序前r的节点形成新的节点集合，然后在新的节点集合中搜索种子节点，选择其中影响力最大的节点作为第一个种子节点；在第二个步骤中，算法在新的节点集合中搜索余下种子节点，其方法与CELF算法在第二个步骤中的方法相似。

3 实验结果及分析

下面的实验将HD＿Greedy算法与其他经典算法进行对比分析，实验包括各个算法分别在NetHEPT和NetPHY中得到的种子节点影响力以及计算时间。

所有实验都在同一台PC机上进行，其中CPU是Intel酷睿双核E7200，主频2.53GH，内存2G。由于当r＝1%时，高节点度贪婪算法性能最优，实验将取r＝0.01的高节点度贪婪算法 （HD＿Greedy＿01）分别在独立级联模型、带权级联模型和线性阈值模型等3个不同信息传播模型上与其它算法进行对比实验，算法包括CELF算法、基于度的算法 （Degree）、NewGreedy算法和MixGreedy算法等。在下列各图中，HD＿Greedy＿01表示选取r＝0.01的HD＿Greedy算法，Greedy表示CELF算法，Degree表示基于度的算法。独立级联模型的节点影响因子p取值与文献[13，14]中一致，均为0.01。

种子节点的数目为50，取值与文献[13，14]一致，另外，为了确保节点影响力的精确性，每个算法对节点的影响力计算20000次，取平均值作为节点最终影响力，以防止随机概率引起的误差。由于Degree算法在寻找种子节点过程中只选取度数最大的节点，不需计算节点的影响力，它的计算时间非常短，约为0.004秒，比其它算法快6个数量级以上，所以在各个算法的计算时间对比时，Degree算法不做比较。

独立级联模型实验

图2为各个算法在独立级联模型中的比较，其中纵坐标为影响力平均值，横坐标为种子节点数目。由图2可见，在NetHEPT和NetPHY中，HD＿Greedy＿01算法与Greedy、NewGreedy和MixGreedy这3个算法得到的种子节点影响力增长曲线几乎重叠，而且最终的影响力相差不到1%，明显高于Degree算法，尤其在NetPHY中，差值达到17%。这说明HD＿Greedy＿01算法得到的种子节点影响力与Greedy、NewGreedy和 MixGreedy三个算法相近，而明显高于Degree算法。从图2还可以看出，HD＿Greedy算法得到的种子节点影响力增长曲线与Greedy算法几乎完全重叠，最终影响力相差很少，这说明所有种子节点几乎都集中在部分度数较高的节点集合中，HD＿Greedy算法只在少部分高度数节点集合中搜索种子节点并不会损失种子节点影响力。

图2 独立级联模型中不同算法影响力对比

图3 为独立级联模型下的算法计算时间对比情况，时间单位为秒 （s）。从图3可见，在NetHEPT和NetPHY中，HD＿Greedy＿01算法相对于Greedy算法计算时间分别缩短了75%和64%，效率大为提高，而且也明显低于MixGreedy和NewGreedy算法的计算时间。实验发现，在NetHEPT和NetPHY中，NewGreedy和MixGreedy算法计算时间不稳定，NewGreedy算法在NetPHY中的计算时间比Greedy算法快了近60%，而在NetHEPT中的计算时间甚至比Greedy算法还要慢，同样的情况也出现在MixGreedy算法中，计算时间的不稳定性不利于算法的性能评估。HD＿Greedy＿01算法不但大大缩短了计算时间，而且具有良好的稳定性。因此，在独立级联模型的算法对比实验中，HD＿Greedy＿01算法性能更好。

带权级联模型实验

图4 给出了各个算法在带权级联模型中的比较，其中纵坐标为影响力平均值，横坐标为种子节点数目。

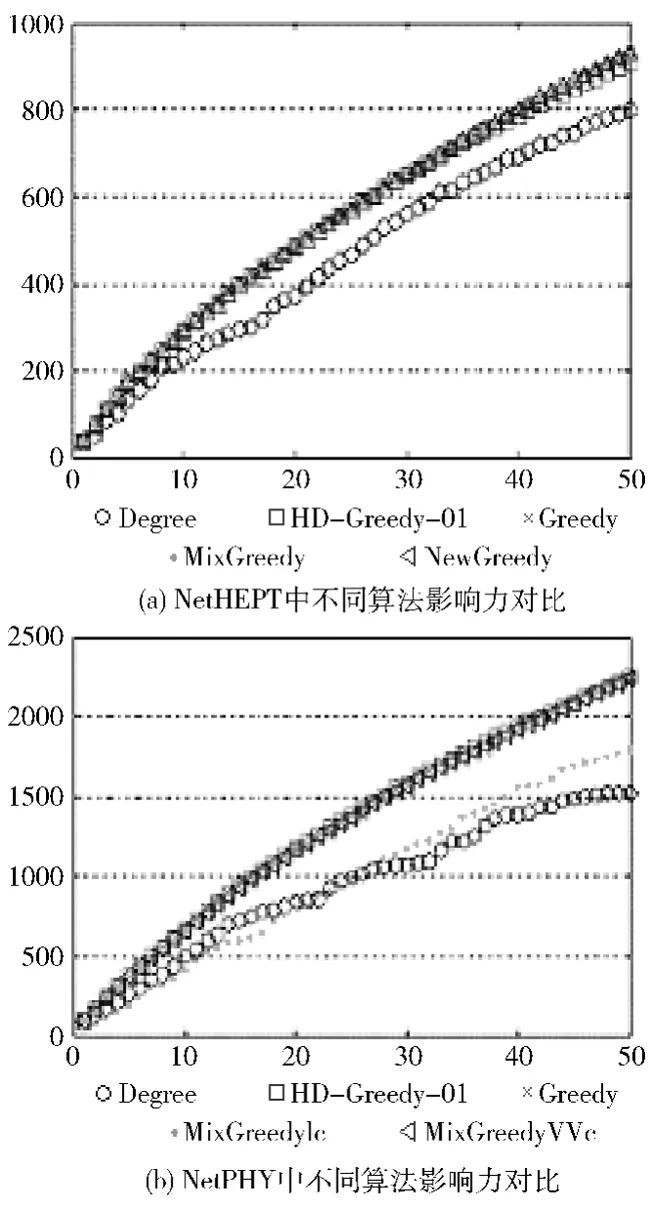
图4 带权级联模型中不同算法的影响力对比

相比于独立级联模型，在带权级联模型中种子节点影响力增大，但 HD＿Greedy＿01算法与 Greedy、NewGreedy和MixGreedy这3个算法得到的种子节点影响力的增长曲线也几乎是重叠的，各个贪婪算法最终的影响力大小差距也不大，不到1.5%。而Degree算法得到的种子节点影响力明显不及贪婪算法，在NetHEPT和NetPHY中分别仅有贪婪算法的85.5%、62.3%。另外，随着网络节点数目增多，Degree算法得到的种子节点影响力与贪婪算法差距也在增大，这也说明Degree算法不适合在大规模社交网络中求解种子节点影响力。

图5是在带权级联模型下各个算法计算时间对比情况，时间单位为秒 （s）。从图5可以看出，在NetHEPT中，HD＿Greedy＿01算法比Greedy算法的计算时间缩短了48.5%，而在NetPHY中计算时间缩短了55.6%。同时它还是速度最快的算法，比次快的MixGreedy算法在NetHEPT和NetPHY中分别快了44.5%和11.2%。NewGreedy算法的计算时间比较长，比Greedy算法还长，在NetHEPT中的计算时间是Greedy算法的244%，在NetPHY中则达到了275%。

图5 带权级联模型中不同算法计算时间对比

线性阈值模型实验

由于NewGreedy和MixGreedy算法是基于独立级联模型提出的，仅适应于独立级联模型和带权级联模型。为了扩展到线性阈值模型中，首先在独立级联模型和带权级联模型中用MixGreedy算法求得种子节点，然后在线性阈值模型中计算种子节点的影响力。为了便于比较，本文与文献[14]的过程一致，其中 MixGreedyIc和 MixGreedyWc分别表示在独立级联模型和带权级联模型下MixGreedy算法得到的结果。

图6是在线性阈值模型中不同算法得到的影响力情况，其中纵坐标为影响力平均值，横坐标为种子节点数目。由图6可见，在线性阈值模型中，HD＿Greedy＿01算法与Greedy算法的种子节点影响力增长曲线几乎是重叠的，MixGreedyWc算法得到的种子节点影响力与它们的相差也很小。Degree算法在NetPHY中得到的种子节点影响力仅为Greedy算法的67.3%。值得一提的是，MixGreedyIc算法在NetPHY中得到的种子节点影响力与HD＿Greedy＿01、Greedy和MixGreedyWc这3个算法相差比较大，达到了23.9%，而在独立级联模型中MixGreedy算法得到的种子节点影响力与其它贪婪算法相差很小。这也从侧面反映了MixGreedy算法在独立级联模型或带权级联模型中得到的种子节点并不能在线性阈值模型中得到很好的扩展。

图6 线性阈值模型中不同算法的影响力对比

4 结束语

在不同信息传播模型中，HD＿Greedy算法得到的种子节点影响力与其它贪婪算法接近，但计算效率有了较大提高。尤其在大规模较的社交网络中，它的计算效率更高，这表明HD＿Greedy算法更适应于大规模社交网络。虽然NewGreedy和MixGreedy算法得到的种子节点影响力与CELF算法非常接近，但存在着计算时间不稳定以及在线性阈值模型中可扩展性较差等问题。而Degree算法得到的种子节点影响力与所有贪婪算法相差较大。因此，在上述算法中，HD＿Greedy算法性能更优。

HD＿Greedy算法也有一些问题有待于进一步研究，比如如何确定高度数节点占所有节点的百分比r值使得算法具有最优的性能，r值设置过小，算法得到的种子节点影响力将受到损失；r值设置过大，算法的计算效率将大大降低；当r＝1时，它完全蜕变为CELF算法。r值的确定与许多参数是相关联的，如社交网络中节点数目及拓扑结构、信息传播模型的影响因子大小以及种子节点数目等，还需要做进一步的研究。

本文针对CELF算法计算时间过长的问题，基于社交网络节点的度呈幂律分布以及节点的度与影响力强关联性，提出了HD＿Greedy算法，通过实验表明，在不同的信息传播模型中，HD＿Greedy算法在保证影响力不受损失情况下明显提高了计算效率，并具有良好的计算时间稳定性和可扩展性。

[1]Nielsen Online Report.Social networks ＆blogs now 4th most popular online activity[EB／OL].http:／／tinyurl.com／cfzjlt，2009.

[2]http:／／news.xinhuanet.com／internet／2010－03／17／content＿1 3186 77.htm[OL].2010.

[3]Shinsuke Nakajima，Junichi Tatemura.Discovering important bloggers based on analyzing blog threads[C]／／WWW 2005 2nd Annual Workshop on the weblogging Ecosystem，2005.

[4]Song X，Chi Y，Hino K.Identifying opinion leaders in the blogosphere[C]／／ACM 978－1－59593－803－9／07／0011，2007.

[5]Weng J，Lim E P，Jiang J.Twitterrank:Finding topic－sensitive influential twitterers[C]／／Proc of the third ACM international conference on Web search and data mining，2010.

[6]Tang J，Sun J，Wang C，et al.Social influence analysis in large－scale networks[C]／／Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2009.

[7]Gilbert E，Karahalios K.Predicting tie strength with social media[C]／／Proceedings of CHI，2009.

[8]Cha M，Haddadi H，Benevenuto F.Measuring user influence on twitter[C]／／ICWSM，2010.

[9]Leavitt A，Burchard E，Fisher D.The influentials:New approache for analyzing influence on twitter[EB／OL].http:／／www.twylah.com／stilescarrie／tweets／245590531631872，2012.

[10]Bakshy E，Hfman J，Mason W.Identifying influencers on twitter[EB／OL].http:／／thenoisychannel／2011／04／16／identifying－influencers－on－twitter／，2013.

[11]Lu L，Zhang Y C，Yeung C H.Leaders in social networks，the delicious case[J].PLoS ONE，2011，6 （6）.

[12]Leskovec J，Krause A，Guestrin C，et al.Cost－effective outbreak detection in networks[C]／／Proceedings of the 13th ACM SIGKDD Conference on Knowledge Discovery and Data Mining，2007:420－429.

[13]Wei Chen，Yajun Wang，Siyu Yang.Efficient influence maximization in social networks.To insert individual citation into a bibliography in a word－processor，select your preferred citation style below and drag－and－drop it into the document[C]／／Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2009:199－208.

[14]Kimura M，Saito K.Tractable models for information diffusion in social networks[C]／／Proceedings of the 10th European Conference on Principles and Practice of Knowledge Discovery in Databases，2006:259－271.