基于核心节点的复杂网络社区划分算法

牛冬冬，陈鸿昶，金 鑫，刘力雄

（1.国家数字交换系统工程技术研究中心，河南 郑州450002；2.国家计算机网络与信息安全管理中心，北京100031）

0 引 言

复杂网络的网络结构存在着小世界特性、无标度特性以及网络节点的幂律分布等特性[1－3]。研究发现，实际的复杂网络并不是随机网络，而是具有一定的组织结构，绝大多数复杂网络的拓扑结构都呈现总体分散局部聚集的特征，即整个网络是由若干个 “群”或 “团”构成的，群内部的节点链接相对较紧密，但是各个群之间的链接相对而言却比较稀疏，研究者把这称为复杂网络的社区结构特性。复杂网络的社区发现对于复杂网络的拓扑结构分析、群体行为分析以及行为预测等具有重要的研究意义。

目前存在很多种社区发现方法，可以分类为全局社区发现方法和局部社区发现方法[4]。全局社区发现方法有图分割方法、层次聚类算法、分裂算法等等，由于全局社区发现方法进行社区发现时利用全局的网络信息，所以该类算法计算复杂度往往过高，而复杂网络的规模愈来愈大，所以该类算法的应用范围比较有限。局部社区发现方法是从点到面的信息挖掘，使用网络中的部分信息进行社区分析，因此有着全局社区发现方法不可比的效率，该类方法一般是选取网络中的一个起始节点进行社区结构的探测，通过发现不同的起始节点所在的社区达到发现全网社区的目的。但是该类社区发现方法的社区发现结果准确度往往较低，因为该类社区发现方法受限于起始节点，当起始节点为边界节点时发现的社区结构并不一定是网络中真实的社区结构。局部社区发现方法虽然降低了计算复杂度，但却是以社区发现质量降低为代价的，因此该类方法的应用也比较有限。

针对上述社区发现方法存在的不足，本文提出一种基于核心节点的社区划分方法。本方法借鉴了从中心节点出发进行社区发现可以保证社区发现质量思想[5]，提出了直接探测出目标网络中存在的属于不同社区的核心节点作为社区划分的种子节点，然后采用相似性传递的节点相似性度量方法计算网络中其他节点与核心节点的相似度，根据相似性度量结果对网络进行划分。本方法在算法复杂度较低的条件下保证了社区发现的质量。

1 算法的相关准备

1.1 网络模型定义

复杂网络可以建模为图G＝（V，E），设网络G具有n个节点和m条边，其顶点集为V＝｛V1，…，Vn｝，边集合为E＝｛Ej｜Ej∈V×V，j＝1，…，m｝。本文中只考虑无向、无权的网络，网络的邻接矩阵A的取值为0或1，若Vi与Vj之间有边相连时Aij＝1，否则Aij＝0。Newman等提出了网络模块性评价函数 （又称Q函数），Q函数定义如下

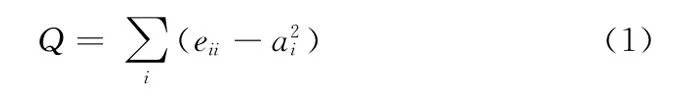
其中，eii是所连接的两个节点均在社区i内的边占网络总边数的比例，ai是有一个节点在社区i的边占网络总边数的比例。社区结构性越弱Q值越小，社区结构性越强Q值越大，目前大多数社区发现算法用模块度作为标准来评价社区划分的好坏。

1.2 相似性度量

相似性度量是对网络图中顶点之间相似或相异程度的度量，相当一部分的复杂网络社区发现算法都利用到了相似性度量，目前对网络中节点的相似性度量已经有了比较系统的研究，大部分的方法都是利用了网络中节点的邻接关系来计算节点之间的相似度，有的方法利用的是全局的邻接关系，有的方法利用的是局部的邻接关系。

一种利用全局邻接关系的节点相似性度量[6]将节点之间的距离定义为

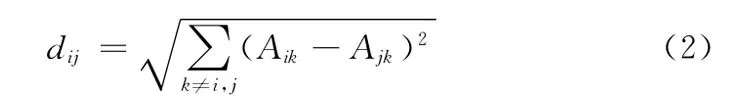
这是一种基于结构同等概念的度量顶点相异度的方法。结构同等是指两个节点的链接关系相同，即两个节点有着相同的邻居节点，若节点i和j结构同等，则dij＝0。这种方法可以计算出网络中任意节点之间的相异度，但是计算的结果有时并不能正确的反映节点之间的相异程度，如图1所示。

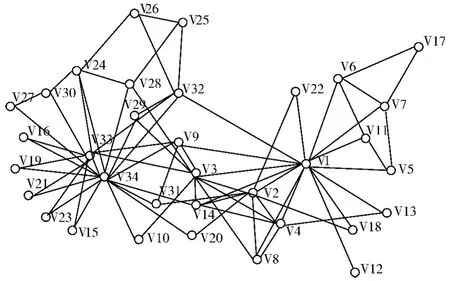
图1 空手道俱乐部成员间的相互关系

采用式 （2）计算出V12与V1的相异度为3.873，而V12与V33的相异度为3.6056，根据计算结果得到V12与V33更加近似，但是图中显然可以看出V12仅与V1有边连接，计算结果显然得出了错误的相异性度量。但是当利用式 （2）计算V33，V1与V34的相异度时，计算结果正确的反映出了节点之间的相异程度。可以发现V12处于网络的边界位置，与该节点的邻居节点个数很少，而V33，V1与V34都是大度数节点，所以发现采用式 （2）往往不能正确得到低度数节点与其他节点的相似度，但可以用于计算大度数节点之间的相似度。

局部相似性度量方法共同特点是利用节点的邻域子图，该类方法认为两个节点共有的邻居节点越多，则两个节点之间就更加相似[7]。节点Vi的邻居节点集记为N（i），即N（i）＝｛Vj｜Aij＝1｝。Vi的星型邻域子图记为St（i），它是由Vi及其邻居点集构成，即St（i）＝｛Vi｝∪N（i）。如图1所示，V6的星型邻域子图St（6）包括5个节点St（6）＝｛V1，V6，V7，V11，V17｝，V6和V7的 星 型 邻 域 子 图 的 交 集St（6）∩St（7）＝｛V1，V6，V7，V17｝。集合St（6）∩St（7）反映了节点之间联系的紧密程度，综上定义Vi与Vj的局部相似性度量[8]为

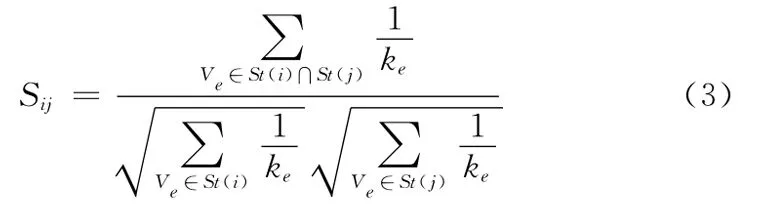
式中，ke为Ve的度数，该方法能够正确的反映两个节点之间的相似程度，但是当两个节点之间的距离大于2的时候，两个节点之间不存在公共的邻居节点，此时采用局部相似性度量方法不能度量这两个节点之间的相似程度。

2 算法描述

2.1 探测网络核心节点

研究发现从中心节点出发可以提高社区发现的质量，通过选取更加合适的起始节点可以提高局部社区发现结果的准确度。通常情况下，在每个社区中往往会有一部分节点处于社区的中心位置，本文定义这部分节点为社区的核心节点，如果在进行社区划分之前可以探测出存在于不同社区的全部核心节点，对接下来的社区划分具有重要意义。

图2是网络G的简单示意图，设网络G中存在着3个社区，不同社区之间用虚线连接。

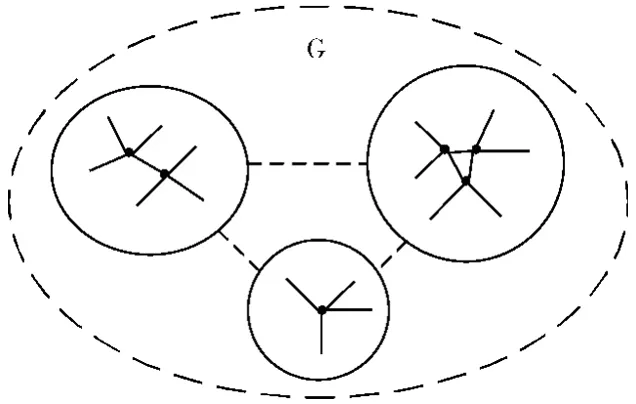
图2 网络G社区关系

如图2所示，不同的社区内部都会存在着一小部分节点处于社区的中心位置，并且会与网络中的其他节点连接关系紧密，该类节点可认为是网络中的核心节点，本文所要探测的核心节点首先是大度数节点。定义网络中节点的集合为V＝｛V1，…，Vn｝，根据网络中节点之间的链接关系计算网络中所有节点的度数，然后根据度数进行排序，定义排序后的节点集合为，然后取出集合中的前一部分节点即大度数节点构成集合，则网络中不同社区内的核心节点一定处于集合中。在本文社区划分算法中需要获取的是每个社区内部唯一的核心节点，然而同一个社区可能有多个大度数节点存在于集合中，所以需要对集合中的节点进行筛选。结合图2进行分析不难得出由于不同社区的核心节点在网络中相距较远，所以对节点进行相似性度量时，同一社区内部的大度数节点相似度一定远大于不同社区内部大度数节点之间的相似度。利用文中式 （2）度量集合中节点两两之间的相似度，将相似度过高的节点从集合中剔除，余下的节点则组成新的集合，该集合即为本文探测出的核心节点集。

2.2 基于相似性传递的节点相似性度量方法

本文进行社区划分时涉及到计算网络中核心节点与网络中其他节点的相似性计算，但是利用式 （2）无法得出正确的相似性度量结果，而利用式 （3）只能度量与核心节点距离小于3的节点之间的相似性，无法度量网络中所有非核心节点与核心节点的相似度。因此需要一种新的相似性度量方法来计算度量网络中核心节点与其他所有非核心节点之间的相似度。本文在局部相似性度量方法的基础上加以改进，提出了基于相似性传递的节点相似性度量方法，具体步骤如下:

步骤1 利用式 （3）计算核心节点与核心节点的邻居节点之间的相似度；

步骤2 采用式 （4）计算核心节点与距离核心节点超过2的节点之间的的相似度

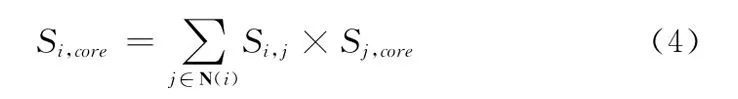
式中，N（i）是Vi的邻居节点，首先采用局部相似性度量方法即式 （3）计算Vi与其邻居节点之间的相似度，将Vi的邻居节点与核心节点的相似度Sj，core作为权值与Si，j相乘，然后求和结果作为Vi与核心节点的相似度。例如图1中定义V6与V1的相似度为S1，6，V7与V1的相似度为S1，7，则V17与V1的相似度即为S1，17＝S1，6×S6，17＋S1，7×S7，17。计算过程中Vi的邻居节点会有一部分距离目标节点更远，这部分节点与目标节点的初始相似度会设置为零，相似性传递过程中这部分节点的贡献也为零。

步骤3 逐层向外计算更外围节点与核心节点的相似度，直到网络中所有节点都计算完毕。

本文提出的这种基于相似性传递的节点相似性度量方法可以正确的度量节点之间的相似性，从式 （4）可以很容易看出与核心节点距离越远的节点与核心节点的相似性会越低，所以该方法不存上述基于全局邻接关系的相似性度量方法错误计算节点之间相似性的缺陷，并且弥补了局部相似性距离不能计算距离大于等于3的节点之间的相似度的不足。

2.3 算法的具体步骤及算法分析

本文算法只需获取网络的邻接关系矩阵即可给出一个较好的社区划分结果，具体的算法步骤如下:

（1）根据网络的邻接矩阵统计出网络中所有节点的度数，并根据节点的度数对节点进行排序，排序后构成集合Vd＝｛Vd1，…Vdn｝；

（2）挑选集合Vd中的大度数节点构成大度数节点集Vmaxd＝｛Vmaxd1，…Vmaxdn｝，本文中选取集合Vd的前0.1部分节点构成集合Vmaxd（实验经验所得）；

（3）利用式 （2）计算集合Vmaxd内节点两两之间的相异性，挑选出相异度大的节点构成集合Vcore＝｛Vcore1，…Vcorek｝，该集合即为核心节点集；

（4）用本文提出的基于相似性传递的节点相似性度量方法计算网络中其他节点与集合Vcore内节点之间的相似度；

（5）根据步骤4的计算结果，将节点划分到其最相似的核心节点所在的社区。

由于复杂网络中节点度数的幂律分布，所以网络中的大度数节点仅占网络规模的很小的一个部分，在探测核心节点的过程中所导致的时间开销应该占算法总时间的很小的一个部分，算法的时间开销大部分耗在了网络中非核心节点与核心节点的相似性度量这一步骤，设网络中存在有n个节点，而探测的核心节点的数目为k，则本方法的时间复杂度应该近似于O（kn），由于k相对于n来说是一个非常小的数值，可以认定为一个常数，因此本方法的时间复杂度近似与n呈线性关系。采用本方法可以对网络中的社区进行比较好的划分，尤其是对于核心节点比较凸显的网络划分效果更好。

3 实验分析

为了测试该算法的性能，在人人网的网络数据和公共的网络数据上进行了社区划分实验。

3.1 人人网数据中的算法应用

本文中采用的网络数据采集于社交网站人人网，其中共有39个个体，已知该网络分为3个小组，其中每个小组内部都会有一到两个 “核心”个体，该个体与其小组内的成员关系密切，如图3所示。

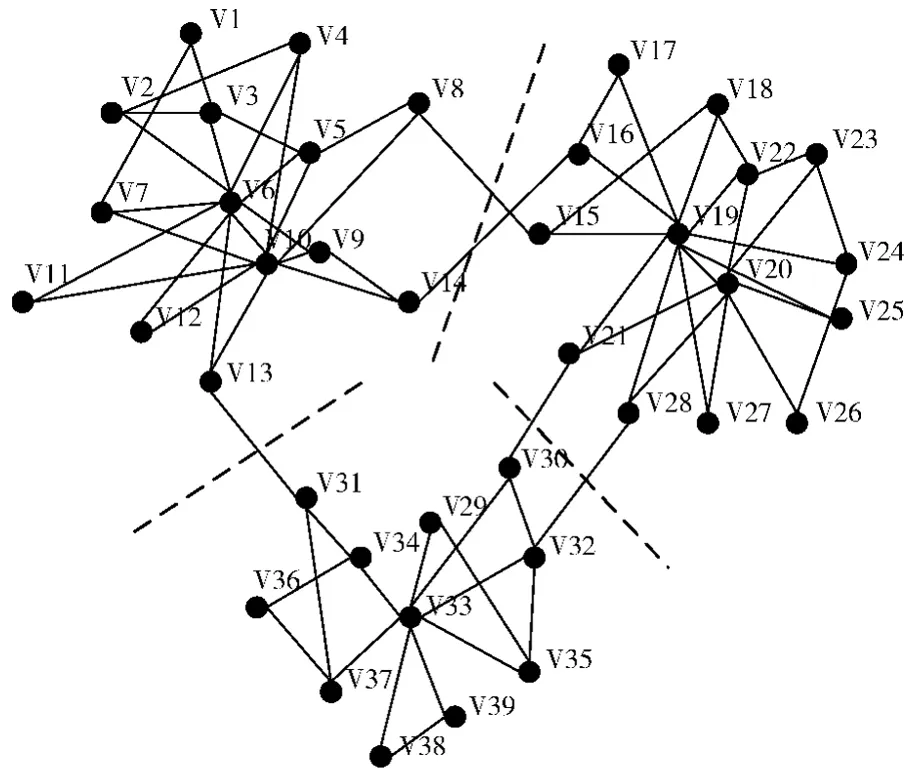
图3 人人网数据网络

该网络是一个核心节点比较明显，且小组之间差异较大的一个网络，本文算法首先根据节点度数对节点进行排序，挑选出V6，V10，V19，V20，V33组成集合Vmaxd，然后计算集合Vmaxd内节点两两之间的相异度，根据计算结果得出V6与V10以及V19与V20之间相异度过低，所以挑选出了V6，V19和V33构成核心节点集Vcore。从图3可以看出，本文算法所挑选的节点正好分别处于3个不同的小组内。在得出核心节点集之后，利用本文提出的相似性度量方法度量网络中其他节点与核心节点之间的相似度，最终对网络进行社区划分得出3个社区，利用Q公式计算社区划分之后的模块度，得到Q＝0.9，将划分的结果与实际的情况进行比较发现所得社区与原来分组情况完全一致。实验结果表明本文算法在核心节点比较明显的网络中可以得到比较理想的社区发现结果。

3.2 公共网络中的算法应用

为了进一步验证算法的有效性和可行性，本文将提出的算法应用在了经典的网络数据集Karate Club网络和Dolphin Social Network中，并且与GN算法和LFM算法[10]进行比较。Karate Club网络是美国20世纪70年代一所大学的一个空手道俱乐部里34名成员之间的友谊关系网络，这是一个存在34个节点和78条边的无向拓扑结构网络。Dolphin Social Network数据集是居住在Doubtful Sound外的一个由62头海豚组成的群落里成员间的频繁交流形成的一个无向网络，这个网络包含62个节点和159条边。GN算法是一种典型的全局社区发现方法，它是通过不断的去除最大边介数的边来达到社区发现的目的；LFM算法是一种典型的局部社区发现方法，它从不同的节点出发基于局部模块度进行信息凝聚来发现社区结构。实验结果如表1所示。

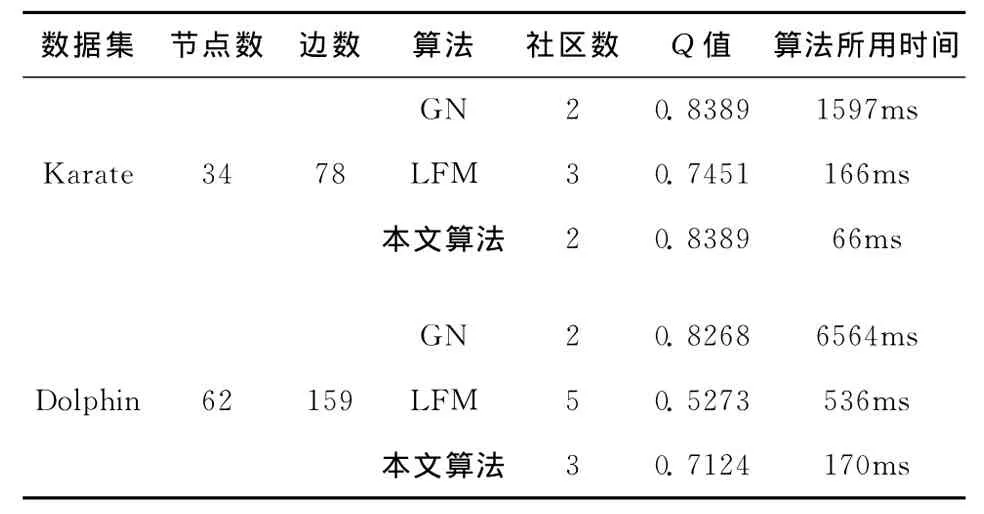
表1 公共网络上的实验结果比较

本文利用模块度Q值这一指标来评判社区划分的质量。从Karate网络的实验结果看来本文算法进行社区划分后得到的Q是0.8389，这一结果与GN算法得到的划分结果一样，而LFM算法得到的Q值为0.7451，本文算法明显优于LFM算法。从表1中可以发现本文算法进行社区划分耗时仅用66ms，而LFM算法用时为166ms，GN算法耗时更是高达1597ms，这一结果说明本文算法复杂度是最低的。分析Dolphin网络的实验结果发现本文算法虽然社区划分质量略低于GN算法得到的结果，但是明显优于LFM算法，并且算法用时仍是最少的。

本文算法将Karate网络划分为2个社区，而将Dolphin网络划分为3个社区，说明在进行核心节点探测时在Karate网络中探测到2个核心节点，而在Dolphin网络中得到3个核心节点。Karate网络中有34个节点，算法用时66ms，Dolphin网络中有62个节点，算法用时为170ms，对这些数据进行分析得到这一式子是算法用时除节点数，再除划分社区个数，这一结果这好验证了本文算法复杂度和网络节点个数以及核心节点个数相关，成线性关系。

由于GN算法在不断的计算网络中最大边介数的边耗费了大量的时间，该算法计算复杂度极高，而LFM算法随机选取初始节点进行社区发现无法保证社区发现质量，本文提出的算法在探测出网络中不同社区的核心节点的条件下进行社区划分，保证了社区发现的质量，并且社区划分过程中仅需计算网络中节点与核心节点之间的相似性，算法复杂度近似与网络中节点个数成线性关系，算法复杂度低。因此理论和实验结果证实利用本文提出的算法进行社区划分是准确并高效的。

4 结束语

本文针对当前节点相似性度量存在的不足，提出了一种基于相似性传递的节点相似性度量方法，可以准确的度量网络中的节点与核心节点之间的相似性，并且应用于本文提出的基于网络核心节点的社区划分方法中。通过多类数据下的实验比较，表明本文提出的算法社区发现质量高，效率高，是一种有效的算法。但是如何更加准确的找出网络中分散在不同社区的核心节点仍是接下来需要重要研究和改进的地方。

[1]Scheffer M.Complex systems:Foreseeing tipping points[J].Nature，2010，467（7314）:411－412.

[2]Van der Leij M J，Goyal S.Strong ties in a small world[J].Review of Network Economics，2011，10 （2）:1－21.

[3]LAI Darong.Reseach of complex network community structure analysis method[D].Shanghai:Shanghai Jiaotong University，2011:4－9 （in Chinese）.[赖大荣.复杂网络社区结构分析方法研究[D].上海:上海交通大学，2011:4－9.]

[4]CHENG Xueqi，SHEN Huawei.Community structure of complex networks[J].Complex Systems and Complex Science，2011，8（1）:57－70 （in Chinese）.[程学旗，沈华伟.复杂网络的社区结构[J].复杂系统与复杂性科学，2011，8 （1）:57－70.]

[5]Chen Q，Wu T T.A method for local community detection by finding maximal－degree nodes[C]／／International Conference on Machine Learning and Cybernetics，2010:8－13.

[6]Fortunato S.Community detection in graphs[J].Physics Reports，2010，486 （3）:75－174.

[7]LüL，Zhou T.Link prediction in complex networks:A survey[J].Physica A:Statistical Mechanics and its Applications，2011，390 （6）:1150－1170.

[8]LIU Xu，YI Dongyun.Complex network community detection by local similarity[J].Acta Automatica Sinica，2011，37（12）:1520－1529 （in Chinese）.[刘旭，易东云.基于局部相似性的复杂网络社区发现方法[J].自动化学报，2011，37（12）:1520－1529.]

[9]Leskovec J，Lang K J，Mahoney M.Empirical comparison of algorithms for network community detection[C]／／Proceedings of the 19th International Conference on World Wide Web.ACM，2010:631－640.

[10]Lancichinetti A，Fortunato S，Kertész J.Detecting the overlapping and hierarchical community structure in complex networks[J].New Journal of Physics，2009，11 （3）:1257－1276.