基于Prim最小生成树算法的时间成本研究

程媛媛

（亳州职业技术学院信息工程系，安徽 亳州236800）

目前，为了解决最小成本的实际应用问题，采用了带权图的最小生成树算法 （prim），该算法由若干条指令对问题进行运算等操作，得出问题的最优解。在程序执行过程中，算法分析和算法复杂度都占有了算法所需的时间。因此，本文针对Prim算法的时间复杂性依使用的数据结构不同，得出在使用数组时时间复杂性为O （V2），使用 （二元）堆结构时为O （EIgV），使用斐波那契堆结构的情况下为O （E＋VlgV）。

1 Prim算法

与Kruskal算法齐名的是最小生成树算法，即Prim算法。Kruskal算法是一条边一条边地考虑，而Prim算法则是一个节点一个节点地考虑。这也算很自然的一种考虑。事实上，凡是涉及图的算法，都可以有按边和按节点进行考虑的不同。

该算法由捷克数学家Vojtěch Jarník于1930年提出，后来被计算机科学家Robert C.Prim于1957年独立发现。[1]1959年Edsger Dijkstra重新发现该算法。因此，该算法有很多名称，如DJP算法、Prim－Jarník算法。

本文从一颗空的最小生成树开始，每一步增加该生成树的尺寸，直到其包括所有节点为止。这种思路就是Prim算法。该算法自然地用到切割属性，如果将所有节点分为2个（分离）集合，则连接2个集合的所有边里面最小的一条边必然属于某棵最小生成树。这样，如果其中一个集合代表正在构建的生成树，另一个集合代表尚未考虑的节点，则每次从尚未考虑的节点里面选取距离正在构建的集合最短（或最近）的节点将是正确的。[2]每次增加生成的尺寸时，只要遵守贪婪的原则，即选择最小的跨越当前最小生成树内外的边，就会正确产生最小生成树。

2 构建最小生成树及Prim算法

可以按照一个节点到其中一个分离集合 （即正在构建的最小生成树）的最短距离来赋值。这个值当然是该节点到给定集合里面所有边中距离最小的值。

2.1 最小生成树问题

在图论问题中，对于连通且没有环路的连通图称为树，这种图可以以任意一个节点为杠杆提起来，而形成一个由上往下的节节分支的倒树形状。[3]在一个连通图里删除所有的环路而形成的树叫做该图的生成树，需要找出的树由于具有最小总权重，因此又被称为最小生成树。[4]最小生成树问题在实际生活中应用非常多，可以在计算机网络、路由控制、公路、电力等网络规划，甚至在人际关系网的构建等方面也提供了一定的帮助。

对这些问题进行抽象，得到最小生成树问题的定义如下：

输入：带权重的连通无向图G＝ （V，E），每条边的权重为Wi。

2.2 算法步骤

（1）构建一个空的最小生成树T，并将所有节点的赋值设为无穷。

（2）选择图G的任意一节点，将其置于欲构建的最小生成树T里，另外一个节点集合为V－T。

（3）对V－T里面的节点的赋值进行修改 （因为T里面多了一个节点，这些距离可能发生变化）。

（4）从V－T集合中选择赋值最小的节点，加入到T里面。

（5）如果V－T为非空，则继续步骤3～5；否则算法终结。

在算法结束时，二元对组 ｛（v，π[v]）｝给出的就是一颗最小生成树。

2.3 算法分析

该算法一开始将所有的节点分解为2个集合：Q和V－Q。一开始V－Q里没有元素，而Q中所有元素离V－Q里元素距离为无穷。然后选择任意节点作为起始节点，并将该元素与V－Q集合里元素的距离初始化为0。之后算法的主要部分就可以开始了。

算法主要由第4步的while循环构成。该循环以队列Q里面是否还有元素作为终结条件。只要Q里面还有元素，算法就继续进行：从队列里面选取离集合最近的元素u加入到集合V－Q里，然后对每个与u有边直接相连的节点进行考虑 （第6行的for循环）。

算法的第8个步骤对节点v到S的距离进行调整。这个调整因为有新加入到S的节点与新加入之间的边长w （u，v）和当前已经计算出的v到S的距离key[v]的相对关系，[5]如果边长小于当前距离，就将当前距离调降为边长。因此，这个步骤也称为降距 （Decrease－Distance）。图1至图6为该算法的一个演示。

根据图1给出的是选取任意节点作为起始节点，将其加入到集合S后的状态。此时除源点到集合S的最近距离0外，其他节点与S的距离都被初始化为∞。[6]然后考察与S里面唯一节点右边相邻的节点，发现7、10、15三个节点，降距其与S的距离后形成图2。

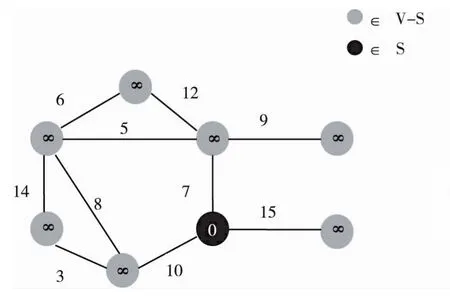
图1 从任意节点开始，其他为∞

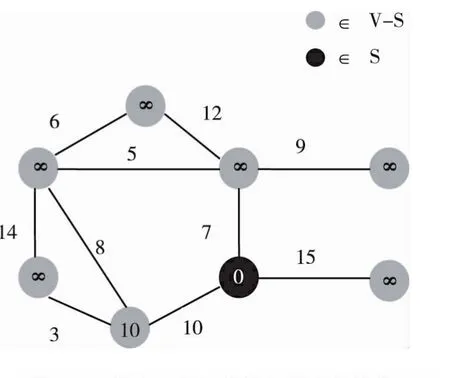
图2 与源点0有边相连的节点被降低

在所有节点里面，按照贪婪策略选取离S最近的节点，即7，加入到S里，并对与节点7有边直接相连的所有节点进行降距，得到图3。然后在所有S外面的节点里选择离S最近的节点，即5，加入到S里，并将于节点5直接有边相连的节点进行降距，得到图4。

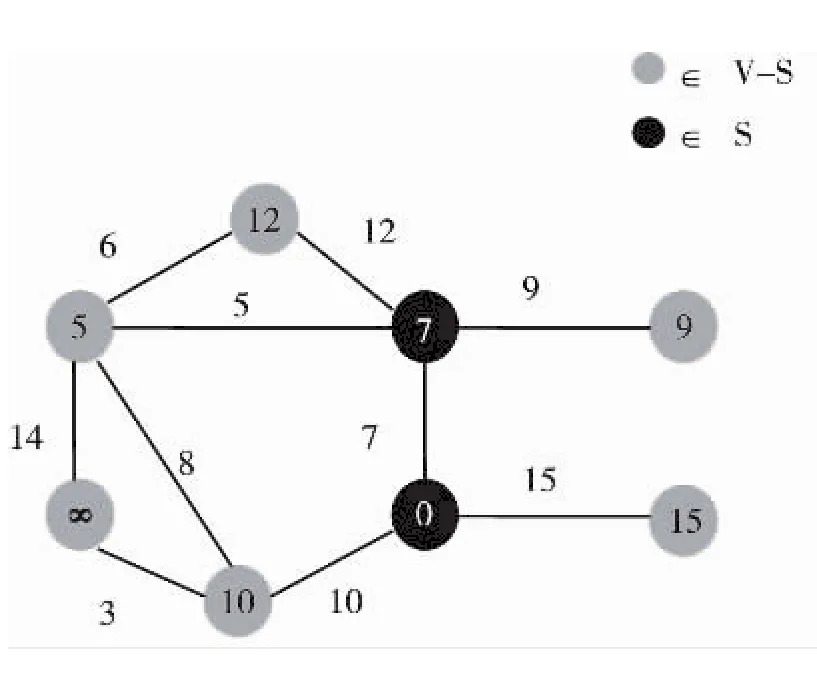
图3 最近的节点7被加入

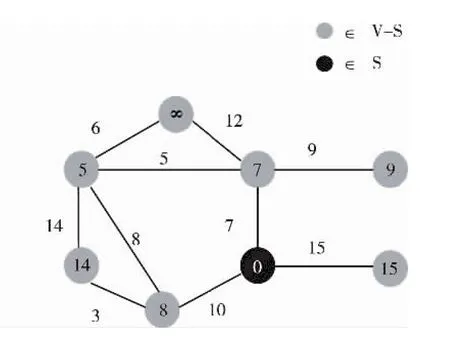
图4 降距相邻节点，加入最近节点5

之后选择离S最近的节点，即6，加入到S中，并降距与节点6直接有边相连的节点的距离，形成图5。这样循环往复，最后得到图6。此时，最小生成树已经完成。

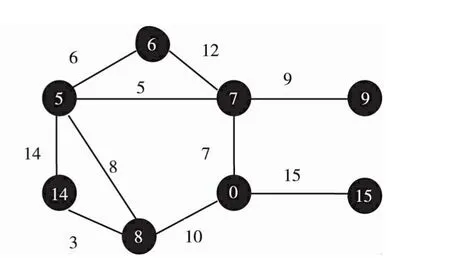
图6 加入节点8、9、14、15后的状态

图5 降距相邻节点，加入最近节点6

3 算法的时间成本分析及结果

3.1 算法的时间复杂度

若要比较不同算法的时间效率，就要确定一个度量标准，最直接的办法就是将计算法转化为程序，在计算机上运行，通过计算机内部的计时功能获得精确的时间，然后进行比较。但该方法受计算机硬件、软件等因素的影响，会掩盖算法本身的优劣，所以一般采用事先分析估算的算法，即撇开计算机软硬件等因素，只考虑问题的规模 （一般用自然数n表示），认为一个特定算法的时间复杂度，只采取于问题的规模，或者说它是问题的规模的函数。[7]为了方便比较，通常的做法是，从算法选取一种对于所研究的问题 （或算法模型）来说是基本运算的操作，以其重复执行的次数作为评价算法时间复杂度的标准。该基本操作多数情况下是由算法最深层环内的语句表示的，基本操作的执行次数实际上就是相应语句的执行次数。一般T（n）Of（n），部分执行语句如下：

则有T（n）＝n的平方＋n的三次方，根据上面括号里的同数量级，可以确定n的三次方为T （n）的同数量级

则有f（n）＝n的三次方，然后根据T（n）／f（n）求极限可得到常数c。则该算法的时间复杂度：T（n）＝O （n的三次方）

O（1）＜O（log2n）＜O（n）＜O（nlog2n）＜O（n2）＜O（n3）＜O（2n）

所以要选择时间复杂度量级低的算法。

3.2 利用时间复杂性对算法的时间成本分析

根据Prim的算法及对算法的分析来对算法的时间成本进行分析。通过上面的算法可以看出，第1～3行的总成本为Θ （V），第6～9行的内循环一共循环节点u的度数 （degree（u））次，第4行的外层循环的次数最多为｜V｜次。因此，该算法的时间复杂性为Θ（V）·TEXTRACT－MIN＋Θ（E）·TDECREASE－DISTANCE

显然，TEXTRACT－MIN和TDECREASE－DISTANCE所需要的时间与实现队列Q所使用的数据结构相关。如果直接使用数组，则每次选取最小元素需要的时间成本为O（V）。而对一个节点进行降距操作为常数时间[8]。因此，在使用数组作为队列Q的实现机制时，Prim算法的总时间成本为O（V2）。

如果使用二进制堆来存放Q的元素，则抽取最小元素的时间成本将降低到O（lgV），但在堆里面对一个元素进行降距操作所需要的时间也是O（lgV），从而导致Prim算法的总时间成本为O（ElgV）。如果图为稀疏图 （即E远远小于V2），则该时间复杂性要好于数组的情况。如果图为稠密图，则时间复杂性接近O（V2lgV），显然不如使用数组的情况。

如果使用改进的斐波那契堆来实现队列Q，则抽取最小元素的成本维持为O（lgV），但降距的时间成本将重新回归到常数时间，从而使Prim算法的总时间成本降为O（E＋lgV），好于数组或二进制堆的情况。这里的摊销成本分析指的是针对一组操作进行最坏情况分析后得出的每个具体操作的成本。因此得出在不同数据结构下，Prim算法的时间复杂性，如表1所示。

表1 Prim最小生成树算法的时间成本

斐波那契堆是一种所谓的 “可归并的堆”（mergeable heap），它实际上是一组堆 （或树）的集合。此种数据结构由于理解困难和编程过程复杂，在实际上并没有多少价值。因此，表1里给出的O（E＋VlgV）摊销时间成本只有理论上的价值。在实际中，Prim算法的时间成本通常被认为是min（O（ElgV），O（V2））。

4 结 语

本文在Prim最小生成树算法的基础上对时间成本进行分析，算法的复杂性决定了时间的复杂性，算法越复杂，在算法运行上耗费的时间越多。针对prim最小生成树算法在运行上，利用了时间复杂度对算法时间成本进行分析，得到了时间成本的结果，为今后在工程应用领域解决问题、选择算法起到了关键性的作用。

[1]丁国强，吕治国.基于Prim算法最小生成树优化的研究[J].甘肃联合大学学报，2009，23（05）：67－69.

[2]武鹏，李美安.具有 O（n）时间复杂度的分布式请求集生成算法[J].计算机应用，2013，33（02）：323－325.

[3]江波，张黎.基于Prim算法的最小生成树优化研究[J].计算机工程与设计，2009，30（13）：3244－3247.

[4]欧阳浩，陈波.求解最小生成树的一种小生境遗传禁忌算法[J].计算机工程与应用，2013，49（01）：59－61.

[5]潘大志，陈友军.Prim算法的一种优化实现[J].西华师范大学学报，2011，32（01）：63－66.

[6]边钊，唐娉，陈趁新.基于阈值约束最小生成树算法的区域合并方法[J].计算机工程与设计，2012，33（01）：229－232.

[7]王会青，陈俊杰，郭凯.启发式初始化独立的k－均值算法研究[J].计算机工程与应用，2012，48（11）：129－132.

[8]任仕玖，宋晖，蒋勋.基于改进Prim算法的变电站巡检机器人路径规划[J].西南科技大学学报，2011，26（01）：61－63.