周期性水位波动作用下库岸滑坡稳定性分析

武 涛

(铁道第三勘察设计院集团有限公司，天津 300251)

水库运行后库区水位的频繁波动，将改变岩土体的有效重度，弱化岩土体力学强度，可能引起滑坡复活或促成新的不稳定斜坡体［1］。

以恩施市双龙洞水库滑坡为研究对象，在充分考虑双龙洞滑坡地质模型的基础上，依据水库的运行条件，利用ANSYS软件的温度模块建立计算模型，并在考虑渗流场与应力场耦合作用的情况下，利用APDL语言编译求解程序，对滑坡进行稳定性评价。

1 滑坡的工程地质条件

该滑坡为中型岩质滑坡，规模600×104m3。地处恩施市珠山镇双龙洞村6组龙洞水库右岸。滑坡平面呈半圆形，剖面呈阶梯状，主滑方向为NE10°，滑坡体斜长300 m，宽600 m，厚度1～22 m，平均厚度约20 m，见图1。

滑坡体表覆盖白垩纪(K)残坡积紫红色碎石土、黏性土等，深度约为0～8 m;下部为三叠系中统巴东组(T2b3)灰绿色碎石土，深度约为8～17 m;滑带埋深:前缘18 m、中部22 m、后缘18 m，厚度约为10～20 cm，主要为灰绿色石块及松散土体;滑床为三叠系中统巴东组(T2b3)紫红色泥质砂岩岩体完整性较好，RQD＞90%，见图2。

图1 双龙洞滑坡全貌

2 数值模拟

利用数值模拟的方法研究滑坡稳定性，要建立合理的数值计算模型，同时还要掌握库水位波动的规律，以及各类岩土参数的合理选取。

2.1 数值模型的建立

根据地质资料，选择主滑面，建立二维计算模型。模型左边界为已知流量边界和水平约束，下边界为“0”流量边界和数值约束，计算模型见图3。

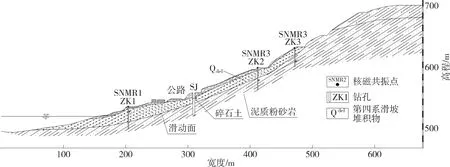
图2 双龙洞滑坡Ⅱ－Ⅱ剖面

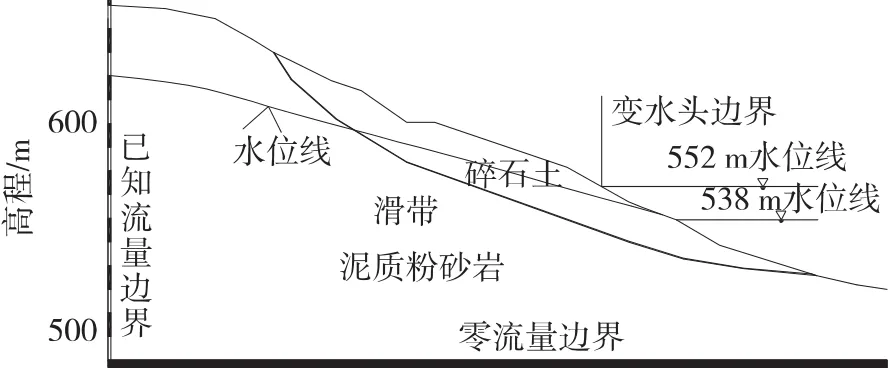
图3 双龙洞滑坡物理模型

2.2 水位运营模型的建立

根据水库历年逐日水位记录表，为了研究水库运行后滑坡稳定性分析，确定了以下模拟方法，见图4。

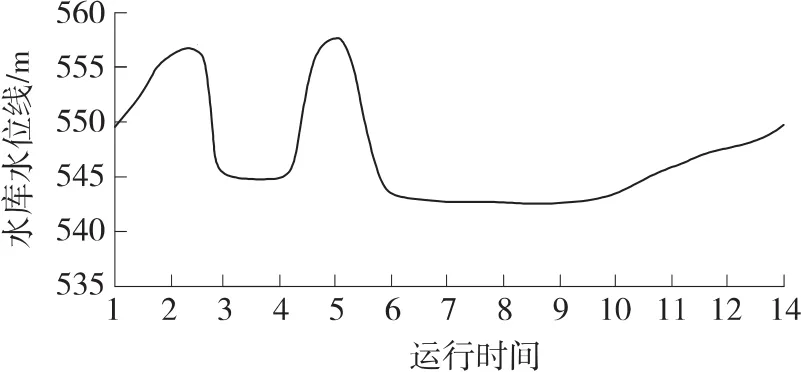
图4 水库水位运行图

2.3 模型参数的确定

根据室内土工试验、原位测试、核磁NMR测试反演结果，滑坡各部位参数见表1及图5。

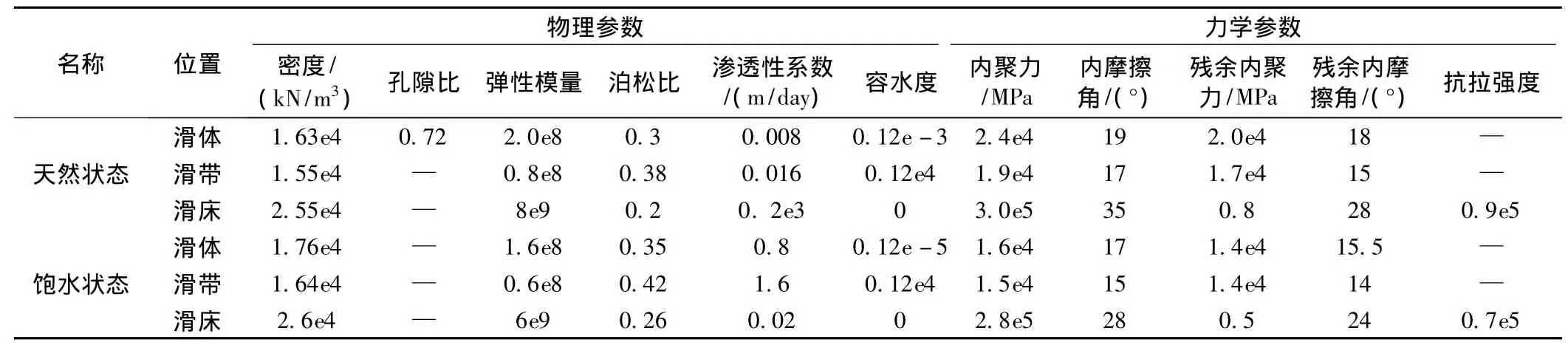
表1 滑坡物理、力学参数

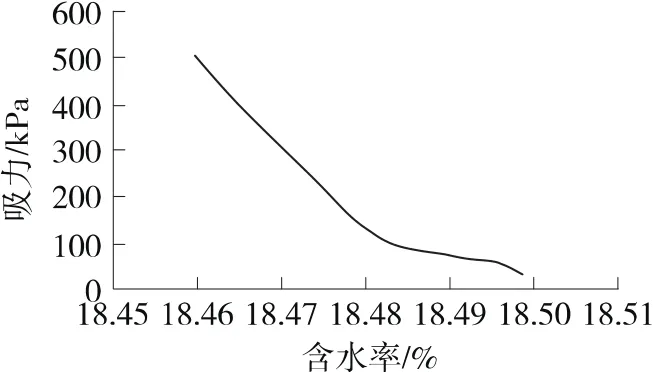
图5 双龙洞滑坡土水特征曲线

3 数值成果分析

为了揭示水位运行对滑坡的影响，分别在滑体、滑带、滑床的前缘、中前缘、中部、中后缘、后缘选取监测点，进行监测。

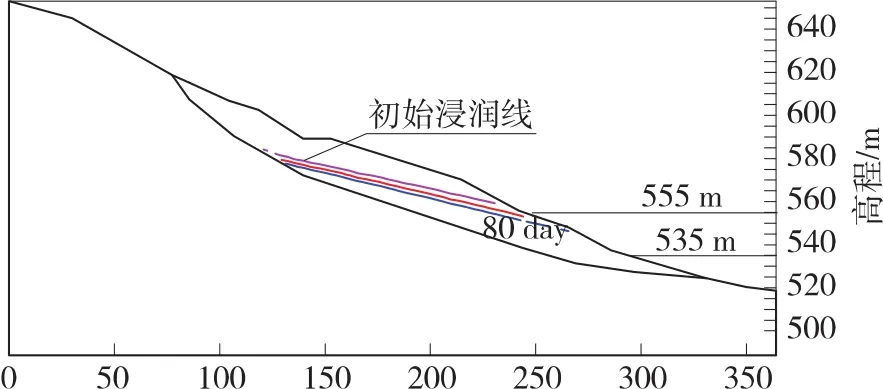
图6 泄水时水位线变动

3.1 渗流场分析

模拟结果分析:

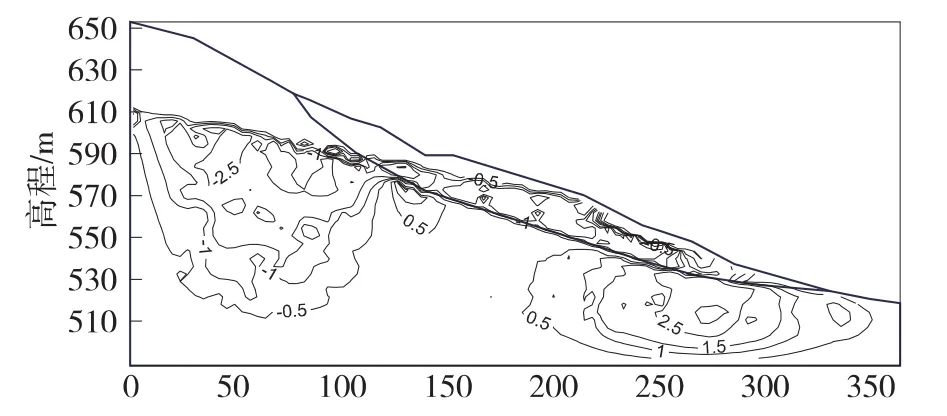
图7 周期1时250 d渗透压力分布

①从图6中可以清晰的看出库水波动引起的地下水的变动主要集中在滑坡的中前缘，而在滑坡后缘由于地下水的补给，变化幅值较小。

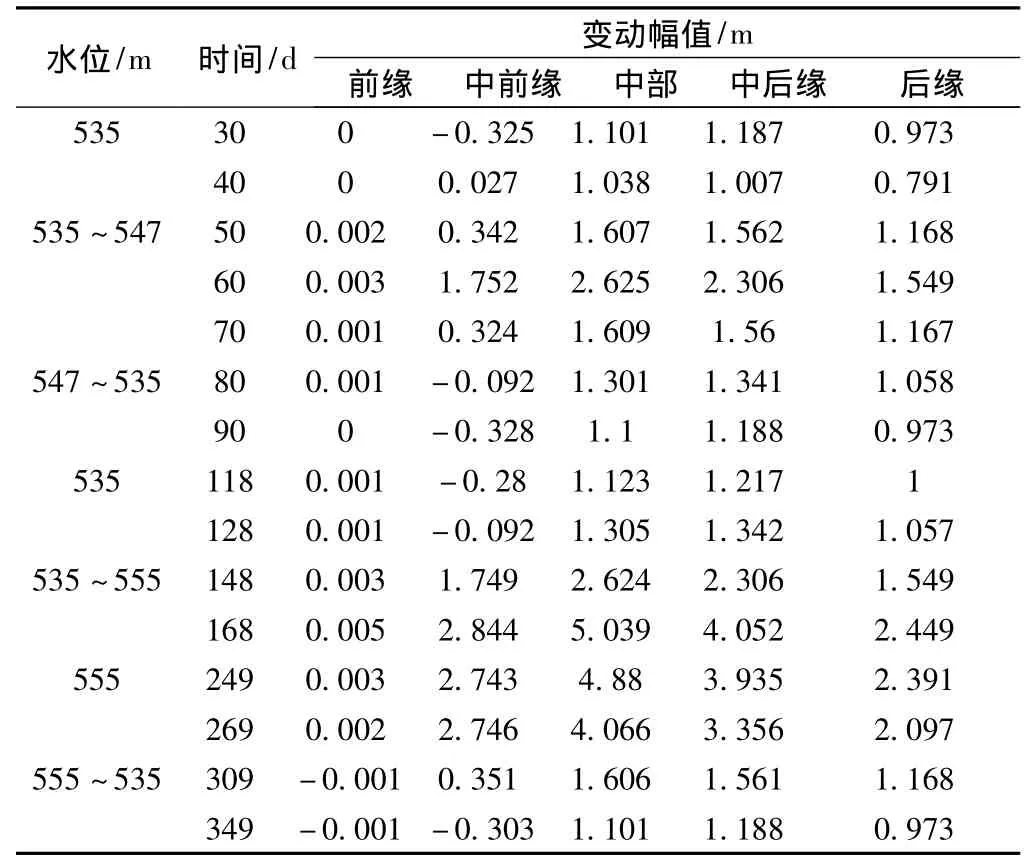
表2 两个周期内滑带水头变动幅值

②在两个波动周期内，在相同位置，后一个周期较前一周期的水头高;在不同的波动周期，滑坡体相同位置，水位变化幅值不同，水头变动幅值最大出现第二个上升期内;由滑带前缘、中部、后缘变化幅值表(表2)可知，地下水变化幅值最大值出现在滑坡的中部附近。

③在不同的波动周期，滑体、滑带、滑床不同位置处的水位变动幅值各不相同。在滑坡中部水位变动幅值最大，底部次之，而在滑坡底部变动幅值最小。如在第二个上升周期(118～168 d)时，滑体、滑带、滑床水位变动幅值分别为4.0 m、3.6 m、2.0 m，其变化幅值逐渐减小。

④在不同的波动周期滑坡体内部水头稳定用时不同，随着波动次数的增加水位稳定用时增加。水位在535～547 m范围内波动时，由于时间短水位未达到稳定，而水位在555 m高程时水位达到稳定，周期一用时为25 d，周期二用时为31 d，说明随库水的波动，地下水位达到稳定的时间越长。

⑤随着库水位做周期性波动，滑坡体内部浸润线的位置也不相同，水位波动次数越多，地下水渗出点位置越高。

⑥由于周期性水位作用时间越长，渗出点位置越高，而相应的非饱和区范围缩小，非饱和区基质吸力贡献范围缩小，不利于滑坡稳定性。

⑦地下水是一条上凸的曲线，当水库泄水时滑坡底部水位线曲率增大，该区域下部水头大于上部水头，渗透力的方向向上;水位周期性波动时间越长，水位线的曲率越大。

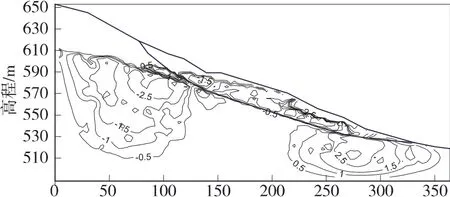
图8 周期2时250 d渗透压力分布

3.2 坡体内部渗透力分析

模拟结果分析:

①水位相同，水位波动周期不同时，渗透力不同，波次数越多，渗透力越大;在两个波动周期内，相同位置处，后一个波动周期的渗透力大于前一个波动周期(表3);不同的波动周期，滑坡体内部相同位置，渗透力增加幅值也不相同。增幅值与水头变化幅值最大值同样出现第二个上升期;从表3可知，变化幅值最大值出现在滑坡的前缘、中前缘，这是因为在该部分水头变化幅值大，相应的渗透压力较大。

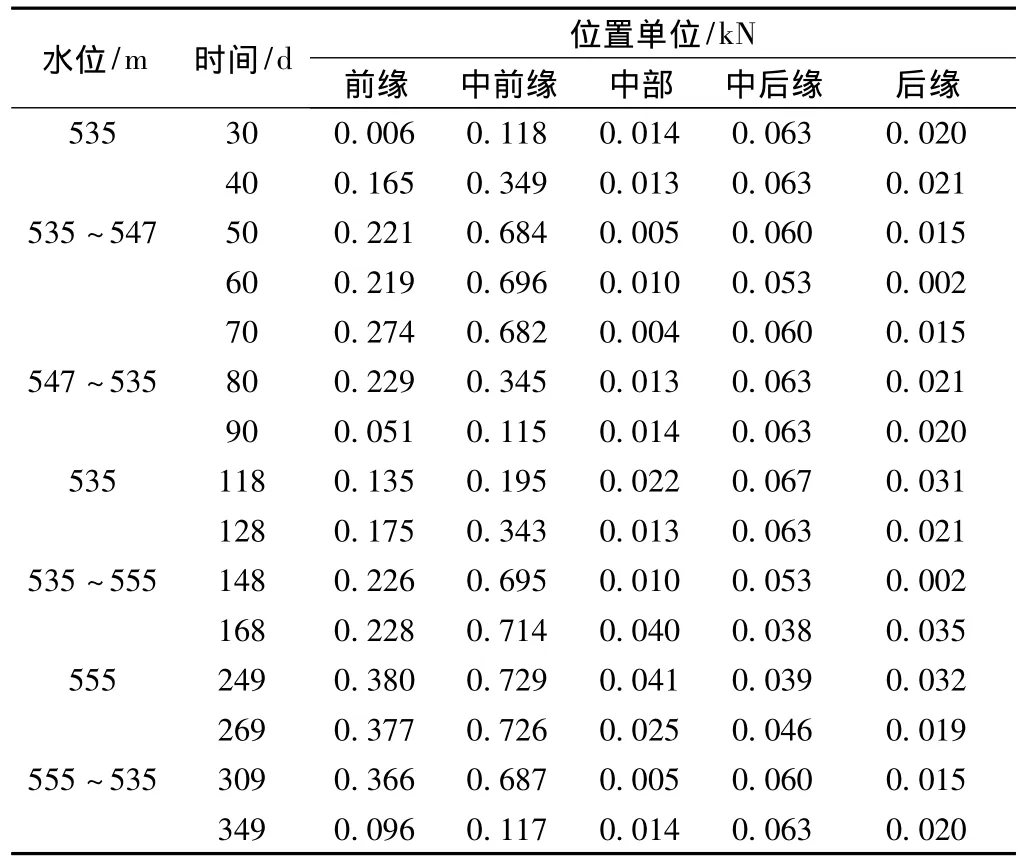
表3 滑带渗透力变动幅度

②在同一个水位波动周期，库水位下降时，渗透力主要集中在滑坡的前缘。库水下降幅值越大，渗透力也越大，滑坡不稳定性也越大。由图7、图8可知，在滑坡体内部，渗透力主要集中在滑坡体前缘，在滑坡体中后缘渗透力的相对较小，同时变幅也较小，且为负值;二者对比可以看出，在滑体部分的渗透力要相应的大于滑带部分的渗透力。在不同的波动周期，滑体、滑带、滑床不同位置处的渗透力的变幅也各不相同;如在第二个上升周期(118～168 d)时，滑体、滑带、滑床渗透力变动幅值分别为0.8 kN、0.5 kN、0.3 kN，其变化幅值逐渐减小。

③下降过程中，渗透力最大值区域逐渐右移，并随库水下降高度的增加而增大，差别较大，滑坡前缘的渗透力要大于滑坡后缘。

④库水波动次数越多，地下水位也下降速度越慢，渗透压力稳定时间也越长，其消散时间上与坡体内部水头稳定用时相同。

3.3 应力分析

①滑带:从图9和图10中可以知水位波动时滑坡体内部的剪应力不断发生变化，在水位初期稳定期(1～30 d)，滑带中前部的剪应力会略微减小，而在滑坡的中后部剪应力会增加，并且随着波动次数的增加，其变动幅度会逐步增大，且在滑坡中部变动幅值最大;在水位波动过程中，水位初期升降对滑坡中前缘影响较大，而在波动后期对其影响较小，剪应力基本维持不变，在滑坡中后缘，水位波动对其影响一直比较显著，且随着波动次数的增加，影响幅度也相应的增大。

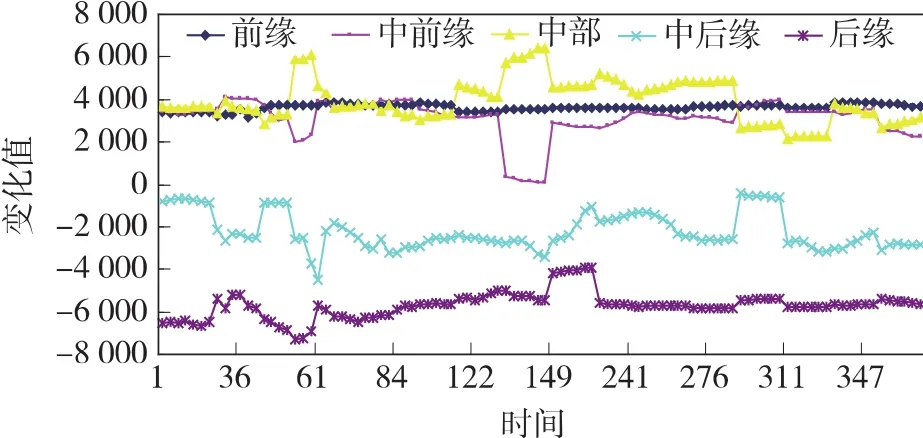
图9 滑床剪应力周期变幅值

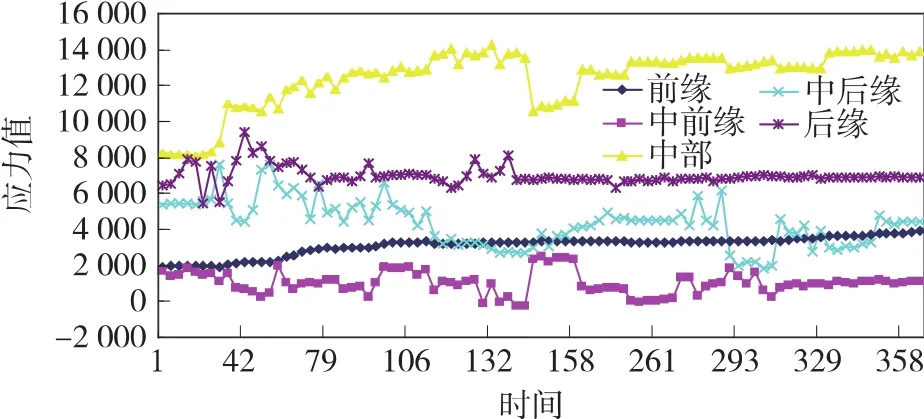
图10 滑带剪应力周期变幅值

②滑体、滑床:相对于滑带而言，滑体、滑床内部的剪应力变化规律有所不同。在水位初始稳定期(1～30 d)，各个部位其剪应力都会有所增大;在水位上升初期(30～40 d)剪应力变化最大;滑带的剪应力主要为正值，而在滑体、滑床后部出现负值;波动过程中，滑体、滑带剪应力的波动幅度相对于滑体而言要大。

③从图11和图12中可以看出，随着水位做周期性的波动，在滑坡的中部、中后缘、后缘剪应力等值线的密度逐步增加，数值增大，并且向滑带附近靠拢，说明双龙洞滑坡的破坏模式为推移是破坏。

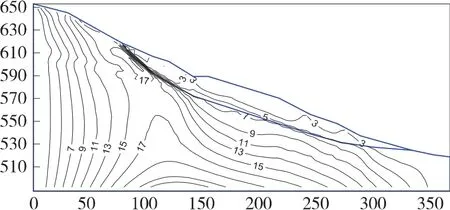
图11 周期1滑坡剪应力等值线

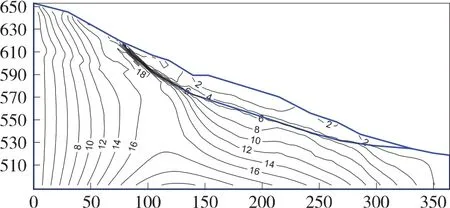
图12 周期2滑坡剪应力等值线

4 结论

本文主要研究目的是周期性库水位波动下滑坡稳定性。利用ANSYS软件中的热传导的温度模块进行渗流分析，利用ANSYS的APDL语言编制将渗透力转化成等效节点力的控制程序;结合双龙洞滑坡工程实例，对该理论进行验证，取得了一些研究成果及结论。

①分析了双龙洞滑坡在水位周期性波动对边坡稳定性的影响。根据水位波动次数的不同水库进行分析，水位分别模拟了波动1次、2次两个周期，得到了滑坡体内水头分布、渗透压力、位移等的变化分布情况，在此基础上对其进行稳定性评价。

②采用有限单元法求解，方法很直接，但是在求解过程中存在一些问题:首先，网格剖分问题，对网格剖分数量限制，模型的单元格尺寸很大导致计算精度不高而出现异常，不满足工程要求，网格剖分过小过密，计算困难，计算时间长，对计算机硬件要求高，浪费时间;再次，在非稳定渗流场中，饱和－非饱和介质的容水度(储水系数)对渗流场的影响很大，容水度大浸润线变化缓慢，容水度小浸润线变化快，而该系数的试验确定方法目前的研究很少。

③对于双场耦合目前研究尚处于起步阶段，各个理论还不成熟，目前数值计算主要以间接耦合为主，能够直接耦合计算的软件目前比较少;间接耦合过程中，计算时步长度的确定是间接耦合的关键。

④库水周期性作用下的滑坡在时间上是一个由多期次的、空间上岩性渐变的复杂的复合地质变形体［5］，作者为了能模拟库水波动时坡体内部耦合效应，作了一些地质模型上的简化，由于硬件的限制仅作了二维研究。在以后研究中，如何建立本质上反映应力场－渗流场耦合三维模型，并进行数值分析，是一个值得深入研究的问题。

［1］胡新丽．三峡水库运行条件下金乐滑坡稳定性评价［J］．中国地质大学学报，2007(32)

［2］武涛．周期性水位波动作用下库岸滑坡稳定性分析［D］．武汉:中国地质大学，2009

［3］何忠泽．滑床渗透性对超覆性库岸老滑坡稳定性的影响［J］．地质科技情报，2012(2)

［4］胡新丽，唐辉明，马淑芝．基于NMR的库区滑坡三维稳定性数值模拟［J］．中国地质大学学报，2006(2):279－285

［5］汪斌．库水作用下滑坡流固耦合作用及变形研究［D］．武汉:中国地质大学，2007

［6］张家发．三维饱和非饱和稳定非稳定渗流场的有限元模拟［J］．长江科学院院报，1997，14(3)

［7］张伟．渗流场及其与应力场的耦合分析和工程应用［D］．武汉:武汉大学，2004

［8］唐辉明，晏鄂川，胡新丽．工程地质数值模拟的理论与方法［M］．武汉:中国地质大学出版社，2000

［9］周彦杰．宝成铁路巨亭滑坡稳定性三维极限平衡分析［J］．铁道勘察，2011，37(4)

［10］马连强．三峡库区张家院子滑坡发育特征及破坏机制研究［J］．铁道勘察，2012，37(3)