基于FPGA的FFT处理器设计

杨伟才，侯 洁，刘玉坤，包莉娜，郭立炜

（河北科技大学信息科学与工程学院，河北石家庄 050018）

高级信号处理算法和硬件的结合广泛应用于现实生活中的各个领域［1－3］。1965年，COOLEY 和TUKEY 发表了一种计算DFT 的快速算法，使得DFT 的计算量大为减少，从而使DFT 得以广泛应用。利用FPGA 灵活的实现方案，产品的低功耗、丰富的逻辑单元、大量的输入输出引脚、内置大量的RAM 和乘法器资源等特点，在FFT 算法的基础上提出了基于FPGA 硬件平台的FFT 处理器设计［4－8］，设计中采用8位有符号数完成256点数据处理，通过减少乘法运算以及采用查表法，加快系统运算速度，提出的数据处理方式避免了浮点运算为数据处理造成的困难，完成了信号处理算法与硬件结合的高速处理方案。

1 FFT算法

一个长度为N的有限长序列的DFT 运算被定义为

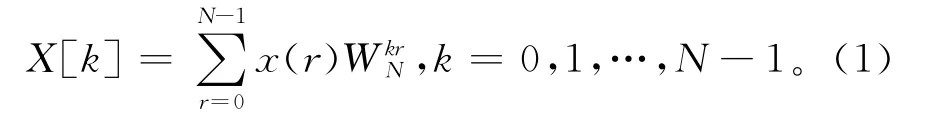
在式中定义W N＝e－j（2π／N）。离散傅里叶反变换为

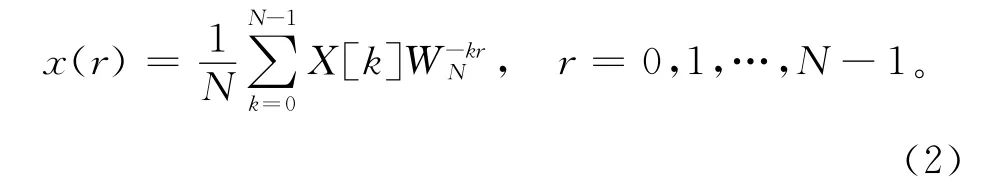
FFT 算法是建立在可以将一个长度为N的序列的离散傅里叶变换逐次分解为较短的离散傅里叶变换这一基本原理的基础上。其大致可分为2类：按时间抽取的FFT算法和按频率抽取的FFT算法。通过研究N为2的整数幂的特殊情况，可以方便证明该算法的原理，因为N为偶整数，所以可以将x（r）分解成2个序列，一个由x（r）的偶数点序列组成，另一个由x（r）的奇数点组成，对于偶数，r用r＝2n代替，对于奇数，r用r＝2n＋1代替，有下式

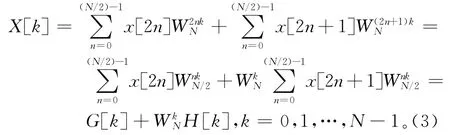
式（3）相当于将原来的N点分解为2个（N／2）点计算，这样就可以认为每个（N／2）点的DFT都可以分解为2个（N／4）点的DFT之和，然后再进行组合，对于一般情况，应当将式（3）继续分解，直到剩下2点为止。利用系数的对称性和周期性还可以进一步减少计算量。

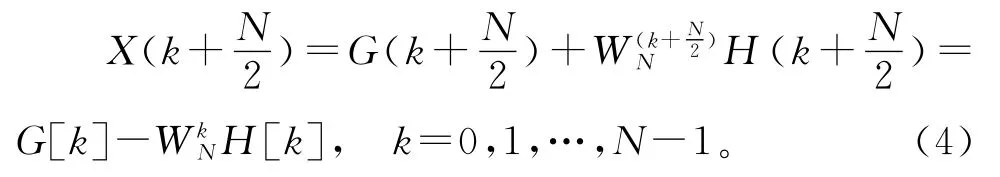
这样，只要求出0 到［（N／2）－1］区间的所有G（k）和H（k），即可求出所有X（k），从而大量减少运算量。笔者只是针对此次设计做了简要论述，关于更详细的算法介绍请参阅文献［9］－文献［10］。

2 FPGA设计

2.1 系统总体设计

本文主要完成了处理器的数据读取、保存、处理和输出模块设计。图1为设计的系统原理图。FFT模块集成了对数据的读取、保存和处理模块，其内部包括3个部分：fft＿process，preramim，FIFO＿Buff。当处理器接收到开始命令时，系统开始工作。工作时首先运行数据输入模块，产生读使能信号和读数据地址，从而控制RAM 将数据虚部存储在preramim 模块中并将数据实部存储在FIFO＿Buff模块。当数据达到要处理点数时，时序控制模块运行，由fft＿process模块将数据分别从preramim 和FIFO＿Buff读取虚部和实部后进行FFT 运算。开始FFT运算后，启动蝶形运算单元，产生存放旋转因子的ROM 单元读信号，经过蝶形运算后将数据重新写入RAM 中存储，同时再次读取preramim 和FIFO＿Buff中的数据，使得整个处理过程得以连续进行，从而减少了运算时间。经过8 级运算后，完成256点FFT 处理，完成后产生输出控制信号，将数据实部存放到asyn＿fifoinst1 模块中。虚部放到asyn＿fifoinst2模块中。最后在selectdatamcu 模块控制下，将实部与虚部结合，顺序输出数据，从而完成处理任务。

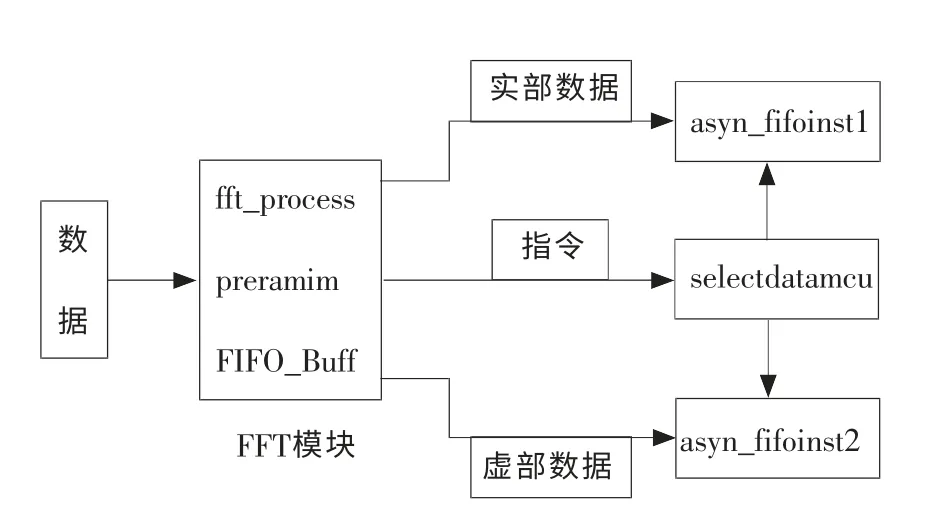
图1 系统原理图Fig.1 System diagram

2.2 FFT控制模块设计

FFT 主控制模块采用FSM（有限状态机）来设计完成，有限状态机是数字系统中的顺序控制电路，在高速运算和控制应用中，状态机有很大的优势。在设计时，首先根据设计的整体功能要求确定所需的状态数量，从一种状态到另一种状态的转移条件以及各状态的输出信号，然后画出状态转移图，从而按照状态转移图编写Verilog程序来实现整个系统的设计功能。关于Verilog语言的学习请参阅文献［11］。图2为此次设计绘制的状态转移图。

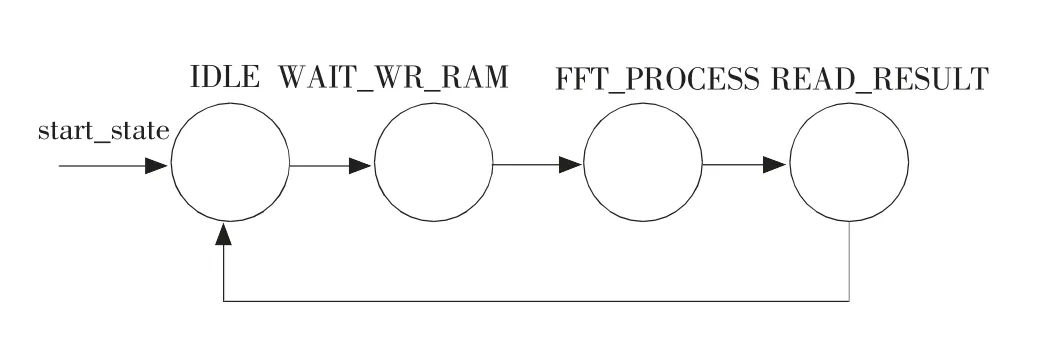
图2 状态转移图Fig.2 State transition diagram

IDLE：fft＿process控制器的初始状态，没有数据输入时，为空闲状态，不进行FFT 运算，此状态还用于一些控制信号的初始化。

WAIT＿WR＿RAM：当有数据输入时，状态机进入wait＿wr＿ram 状态。在wait＿wr＿ram 状态下，通过时钟clk＿fpga的驱动，当FIFO＿Buff的空标志stack＿empty不为0时，从FIFO＿Buff和preramim中将数据写入rama中，数据是由8位I／O 数据口传送得到。在此设计中，FFT 处理器采用了2个时钟，一个clk＿fpga时钟和一个外部写入时钟。数据的传送接收是以外部时钟控制写入FIFO＿Buff中，一上电，FFT 中的FIFO＿Buff接收到第1 个数据后，就会启动读数据。因为读写数据的速度不一样，所以采用异步FIFO 设计，将256个数据全部写入rama中后，状态机进入FFT＿PROCESS状态。

FFT＿PROCESS：在此状态中，将接收得到的数据进行处理，数据存储器采用的是双端口RAM，将256个数据的地址分配，前128个数据为一组，存放地址为0到127，后128个数据为一组，存放地址为128到255，最后将数据送入butterfly中进行蝶形运算，要完成整个FFT 处理过程总共需要8 级处理，每一级处理需要调用128次蝶形运算，在数据处理过程中有2 个双输入输出的256 位数据存储器rama和ramb，这2个数据存储器相互交换来存储数据，使设计不会在存储时发生冲突或数据重叠，同时还可以提高FFT 的数据处理速度。在8级运算中的0，2，4，6级处理时，从rama中读取数据，将处理后的蝶形数据依次存储在ramb中的n和（n＋1）地址中；在1，3，5，7级数据处理时，从ramb中读取数据，将处理后的蝶形数据再依次存储在rama中的n和（n＋1）地址中；8级运算完成之后，进入下一状态。

READ＿RESULT：读数据状态，此次设计采用基2蝶形运算的最优架构，计算中采用同址运算，蝶形运算输出的结果为倒位序，所以最后读数据时要控制ram 地址，将ram 地址进行倒序排列后即可得到输出数据的正序列。

2.3 蝶形运算单元

在FFT 算法中，蝶形运算单元是最为核心的关键部分，从某一级到下一级的计算过程中，基本的计算如图3所示，即先用前一级的一对数值计算得到该级的结果，其中的系数总是W N的幂，而其指数总是相差N／2。由于流图的形状像蝴蝶，因此这种运算称为蝶形运算。式（5）、式（6）为蝶形运算的计算公式。

（cosθ－jsinθ）（C＋jD）项展开式为（Ccosθ＋Dsinθ）＋j（Dcosθ－Csinθ），其中实部为Ccosθ＋Dsinθ＝（C－D）cosθ＋D（cosθ＋sinθ），虚部为Dcosθ－Csinθ＝C（cosθ－sinθ）－（C－D）cosθ。

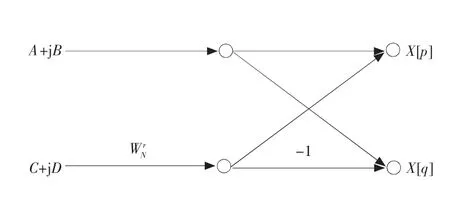
图3 蝶形计算流图Fig.3 Flow of butterfly calcuation

式子经变换后实部与虚部有公共项（C－D）cosθ，经过上述处理后，可以看到在一次蝶形运算中可以减少两次乘法操作，在设计中采用查表法设计旋转因子，将cosθ，cosθ＋sinθ，cosθ－sinθ数值计算出来存储在ROM 中，在计算过程中直接调用这些数值来完成相应计算，使FFT 处理时间大为减少，提升了系统的工作频率。

笔者设计的蝶形运算是由Butterfly 模块完成，该模块首先从数据存储器rama中取出2 个数据的实部和虚部，将它们分别与ROM 中存储的旋转因子相乘，将结果存储在ramb中，在数据处理时，将旋转因子乘以128 之后再存储在9 位的ROM 中，由于一个9位数与一个8位数相乘结果是17位数，在计算中，舍弃数据的低7位，在取数的同时将数据缩小了128 倍，从而避免了浮点运算带来的问题。

3 系统仿真

在完成系统整体设计后，采用Altera 公司的cycloneⅡ系列EP2C8Q208芯片实现系统功能，利用quartusⅡ软件对设计进行编译、综合以及布局布线，由报告显示，此次设计共使用逻辑单元876个，占芯片逻辑单元总数的11%，使用存储器36 352位，占芯片存储器位数的22%，并使用了3 个嵌入式乘法器。在蝶形运算设计完成后，用RTL VIEWER 查看综合后的原理图如图4所示。

系统各模块在设计过程中采用quartusⅡ自带仿真器进行仿真，图5为蝶形运算模块仿真图，从仿真图中可以看出，完成一次蝶形运算需要4个时钟周期，仿真中，笔者输入的数据为A＝are＿in＝0001＿

0101，B＝aim＿in＝0000＿0000，C＝bre＿in＝0000＿1010，D＝bim＿in＝0000＿0000，ROM 地址为rom＿addr＝00010，查表后得cos＝0111＿1100，cos－sin＝001100011，cos＋sin＝010010101，其中，各数据最高位为符号位，将计算结果代入蝶形计算公式，经计算，X（p）＝cre＿out＋jcim＿out＝00011110＋j11111110，X（q）＝dre＿out＋jdim＿out＝00001100＋j00000010，与仿真结果一致。

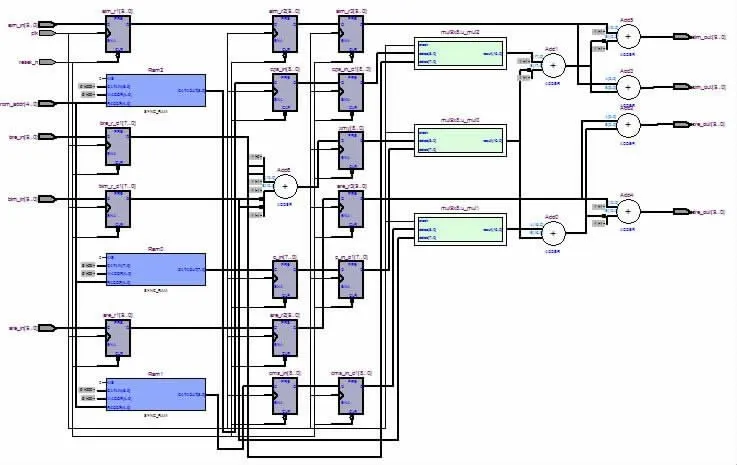
图4 RTL视图Fig.4 RLL view

图5 蝶形运算仿真图Fig.5 Simulation of butterfly operation

对输入信号y＝50sin（400πt）＋50sin（200πt）进行采样，将采样后数据进行处理，并将处理后的仿真波形保存为.tbl文件。用Matlab软件生成频谱数据图见图6，此仿真结果显示与数据处理结果一致。

4 结 语

此次设计使用Verilog HDL 语言进行程序设计，详细介绍了数据从外部输入经过存储到内部处理再到输出的详细流程，给出了系统的整体设计思路以及蝶形运算每一关键点的详细设计说明，并在quartusⅡ8.0软件上进行编译、综合和布局布线，最后下载到cycloneⅡ芯片上完成设计。经过仿真验证，本设计成功实现了8 位有符号数的256 点基2FFT的数据处理，在采用特殊方法设计蝶形模块后，使系统处理速度优于一般FFT 处理器，避免了浮点运算为数据处理造成的困难，完全符合设计标准。

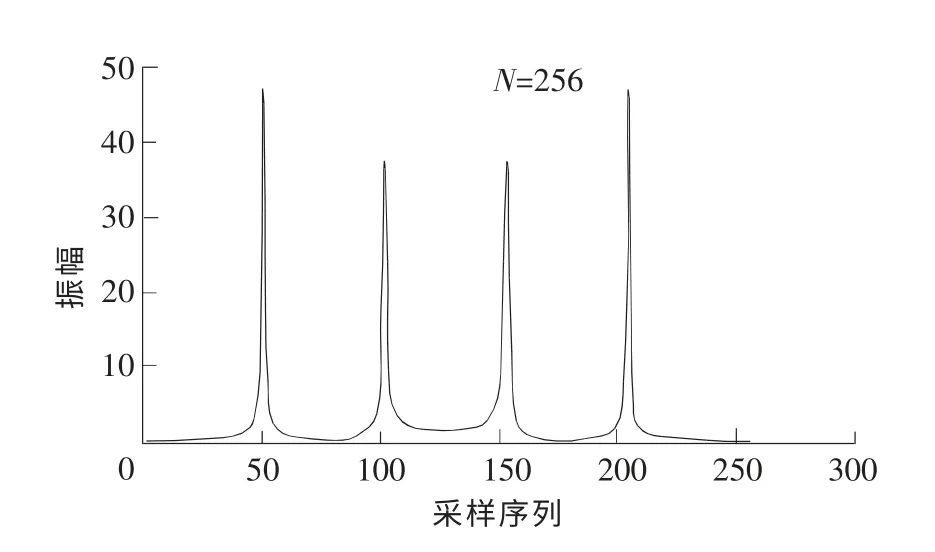
图6 Matlab仿真图Fig.6 Matlab simulation

／References：

［1］ 刘德亮，王竹林，尉广军.基于FPGA 高精度频率测量仪的设计［J］.河北工业科技，2010，27（1）：29－31.LIU Deliang，WANG Zhulin，YU Guangjun.Design of highaccuracy frequency measuring instrument based on FPGA［J］.Hebei Journal of Industrial Science and Technology，2010，27（1）：29－31.

［2］ 张 阳，王中阳，王红胜，等.基于FPGA 的多端口存储控制器设计［J］.河北工业科技，2010，27（6）：401－405.ZHANG Yang，WANG Zhongyang，WANG Hongsheng，et al.Design of multi－port memory controller based on FPGA［J］.Hebei Journal of Industrial Science and Technology，2010，27（6）：401－405.

［3］ 王晓君，陈 禾，罗跃东.一种EW 接收机信号处理系统的设计与实现方法［J］.河北科技大学学报，2007，28（2）：142－146.WANG Xiaojun，CHEN He，LUO Yuedong.Design and implementation of signal processing system for electronic warfare receiver［J］.Journal of Hebei University of Science and Technology，2007，28（2）：142－146.

［4］ NIBOUCHE O，BOUSSAKTA S，DARNELL M，et al.Algorithms and pipeline architectures for 2－D FFT and FFT－like transforms［J］.Digital Signal Processing，2010，20（4）：1 072－1 086.

［5］ ZHOU Yuan，NORAS J M，SHEPHERD S J.Novel design of multiplier－less FFT processors［J］.Signal Processing，2007，87（6）：1 402－1 407.

［6］ CABAL－YEPEZ E，CAROZZI T D，ROMERO－TRONCOSO R J，et al.FPGA－based system for frequency detection of the main periodic component in time series information［J］.Digital Signal Processing，2008，18（6）：1 029－1 044.

［7］ 钟冠文，卢亚伟，付欣玮，等.基于FPGA 的1024 点高性能FFT 处理器的设计［J］.微计算机信息，2012，28（8）：66－67.ZHAON Guanwen，LU Yawei，FU Xinwei，et al.Design of 1024－point FFT processor based on FPGA［J］.Microcomputer Information，2012，28（8）：66－67.

［8］ 唐鸿武.基于FPGA 的感应电机特性分析硬件单元的设计［D］.石家庄：河北科技大学，2010.TANG Hongwu.Design of the Hardware Unit Based on FPGA of Characteristic Analysis on Induction Motors ［D］.Shijiazhuang：Hebei University of Science and Technology，2010.

［9］ 奥本海姆A V，谢弗R W，巴克J M.离散时间信号处理［M］.第2版.刘树棠，黄建国，译.西安：西安交通大学出版社，2001.OPPENHEIM A V，SCHAFER R W，BUCK J M.Discretetime Signal Processing［M］.2nd ed.Translated by LIU Shutang，HUANG Jianguo.Xi′an：Xi′an Jiaotong University Press，2001.

［10］ 程佩青.数字信号处理教程［M］.第3版.北京：清华大学出版社，2007.CHENG Peiqing.Digital Signal Processing Tutorial［M］.3rd ed.Beijing：Tsinghua University Press，2007.

［11］ 刘 波.精通Verilog HDL 语言编程［M］.北京：电子工业出版社，2007.LIU Bo.Proficient in Verilog HDL Language Programming［M］.Beijing：Publishing House of Electronics Industry，2007.