基于状态空间模型的脑电去伪迹与节律提取

黄丽敏，郝崇清，李 斌

（1.河北科技大学现代教育技术中心，河北石家庄 050018；2.河北科技大学电气信息学院，河北石家庄 050018；3.中国民航大学航空自动化学院，天津 300300）

脑电中节律活动的兴奋性异常是某些认知、思维或精神疾病的表征。节律特征已被用于麻醉深度的检测［1］、睡眠分期［2］、疾病诊断与预测［3－4］等。包含节律成分的脑电时间序列往往被工频、眼电和噪声等伪迹污染。因此，能快速提取脑电的节律成分并同时能够去除脑电伪迹对脑电研究具有重要意义。

利用分析法将脑电信号分成多个成分，然后减去其中的伪迹成分，是实现伪迹去除的常用方法。常用的时间序列分解方法主要有独立成分分析（ICA）、小波分析法等。ICA 方法是通过将各种源信号看成是相互独立的源成分，是一种多变量分析方法，在去除脑电伪迹中已经取得了良好的结果［5－8］。但ICA 只能得到同时间序列的变量维数相等数量的成分，即要求盲源数和传感器数量相等，这在成分数量大于时间序列个数时显得无能为力。小波分解方法也是近来应用于脑电去伪迹和特征提取的常用手段，然而如何选择小波母函数才能达到最好效果仍是一个有待解决的研究问题。

状态空间方法是把时间序列看成是由趋势项、周期项和随机波动项组成的混合成分信息。建模过程是基于自回归滑动平均模型（ARMA）与状态空间模型之间可以相互转换［9］。首先是对时间序列建立ARMA 模型，然后将ARMA 模型表示成状态空间并联隔间形式，利用Kalman滤波器进行状态估计，估计出的状态即是分解出来的成分。状态空间解耦已成功应用在经济［10－11］、麻醉深度估计和心电分析［12－13］上。本文利用状态空间方法实现对单导和多导闭眼静息脑电进行节律提取和去噪。

1 状态空间估计

考虑如下ARMA（p，p－1）模型：

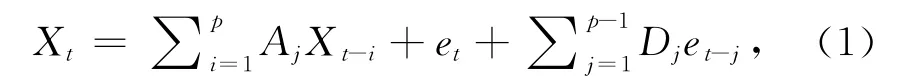
其中：Aj，Dj是模型系数；Xt是模型输 出；et是零均值白噪声。

分别利用ICA准则和极大似然估计确定模型的阶数和模型参数。任一ARMA过程都有一个状态空间描述与之对应，相反，任何状态空间过程也可以用ARMA的形式来表达。因此可以将ARMA 模型转换为状态空间模型。其中ARMA（2，1）模型为

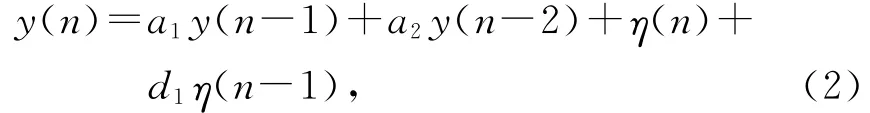
此式可看成噪声作为系统输入的第2类单自由度振动系统。令

可将式（2）写成状态空间形式：

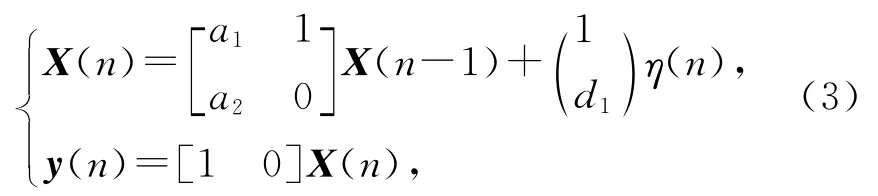
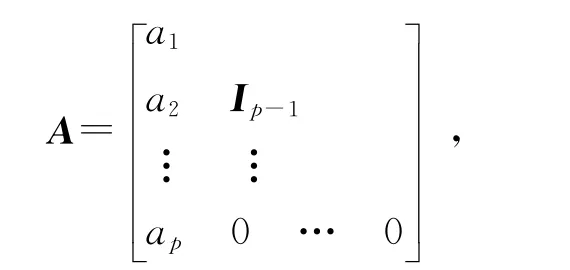
其中Ip－1为p－1阶单位阵，A称为友矩阵。

由于系统状态空间表达的非唯一性，同一系统在经非奇异变换后系统特征值的不变性，说明特征值描述了系统的本征信息，所以求取矩阵A的约当标准型。对实际观测信号而言，求出的特征值是实特征值和共轭复特征值对的集合。共轭复特征值对可看成系统固有频率的阻尼振荡，为把含有复特征值的矩阵简化，避免矩阵中出现复数，对含有复特征值的项进行模态化。假定一组共轭复特征值为ρ（cosφ±isinφ），则模态矩阵表示为

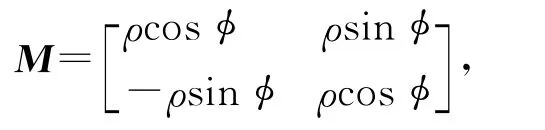
经线性变换后还可写成

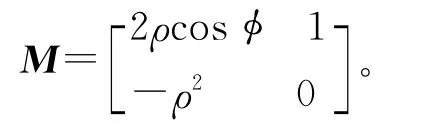
其表示的共振频率为f＝（fs／2π）arctanφ，其中fs为采样频率。对于标准型矩阵A写成如下约当标准型：

共有m个模态矩阵和n个实特征值，的维数为（2m＋n），则多输出系统状态空间模型描述为

其中η（n）为系统噪声，假定它符合多变量高斯分布，η（n）～N（0，Q）；ε（n）为泛化模型形式加入的观测噪声，ε（n）～N（0，R），假定两者的协方差阵皆为对角阵：

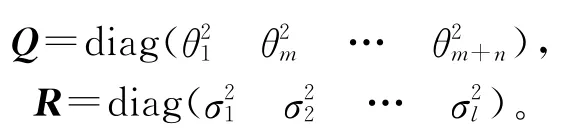
取为如下特殊形式矩阵：

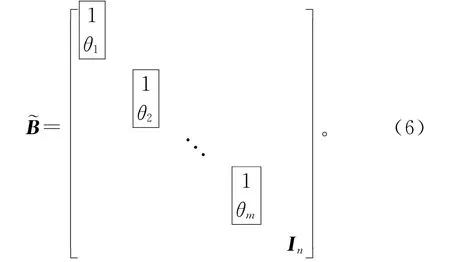
单变量输出时取为

其中In为n阶单位阵，m，n分别为矩阵A中共轭复特征值对和实特征值的个数。如果将Q矩阵归一化，则具有如下形式：

一般状态空间模型可看成由m个ARMA（2，1）模型和n个AR（1）模型组成的（m＋n）个子模型的并联模型，其中AR（1）为一阶自回归模型，具有这种结构的状态空间模型称为隔间模型［11］（compartment model）。对于l维多变量测量时间序列，观测矩阵写成以下形式：

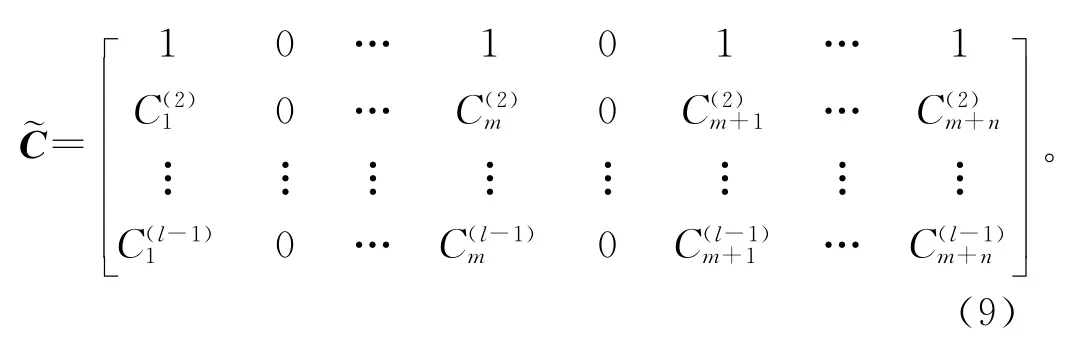
根据以上建立的状态空间模型，利用Kalman滤波器对状态进行递推估计，在状态和噪声都是高斯的情况下，Kalman滤波估计是最优的，此时估计出的状态即是相互独立的各成分分量。

2 实例分析

实验数据为健康志愿者FP1，FP2，F3，F4导脑电时间序列，如图1所示。采样频率为500 Hz，可见序列为非平稳，含有眼电干扰，由图2功率谱可见含有工频干扰以及alpha节律。

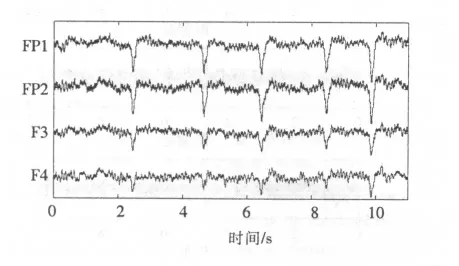
图1 脑电时间序列Fig.1 Time series of EEG

分别给出单变量和多变量时间序列的实例，在单变量实例中，利用ARMA 模型来拟合图1中的F4导数据，并给出不同模型阶数对估计结果的影响。在多变量实例中，对四导数据进行同时处理并将结果与独立成分分析进行对比分析。

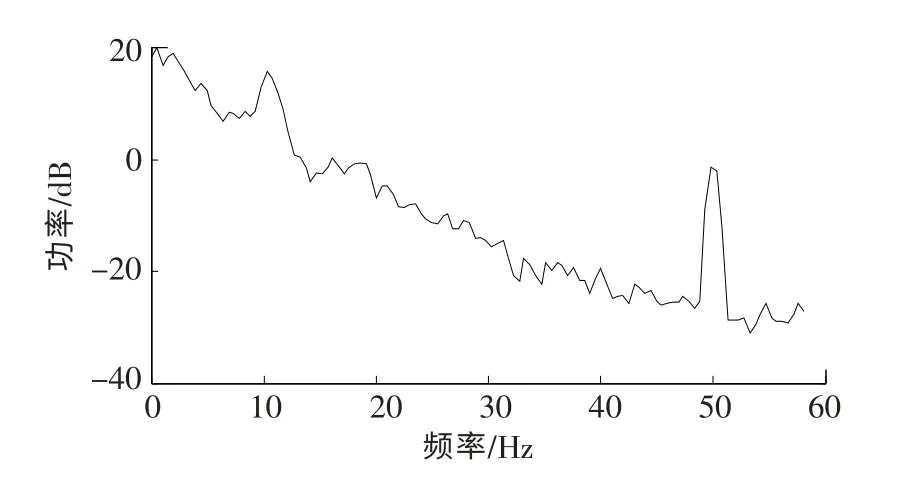
图2 F4导脑电功率谱图Fig.2 Power spectrum of F4lead

2.1 单变量序列

截取F4导的前10s数据，使用两种不同的模型阶数分解实验数据来说明其对估计结果的影响，当模型阶数不足以分解出足够的成分时可以增加阶数。由于在递推估计的初始阶段存在不确定性，所以结果中截取了前100个数据。

当取ARMA（3，2）时，估计出两种成分，如图3所示。ARMA（3，2）由1个ARMA（2，1）模型和1个AR（1）模型并联组成。前者对应一种本征频率，即成分C1对应的特征值为0.583 6±0.809 0i，其频率49.73Hz为工频伪迹。估计出的成分数实际上是3个，其中复特征值对应的成分有2个，但这2个成分频率和幅值是相同的，两者之间仅差一个相位差，仅将其看成1个成分，其他数据的估计结果类似。成分C2仍然包含眼电伪迹、alpha节律和其他成分，要想得到更多的成分需取更大的模型阶数。

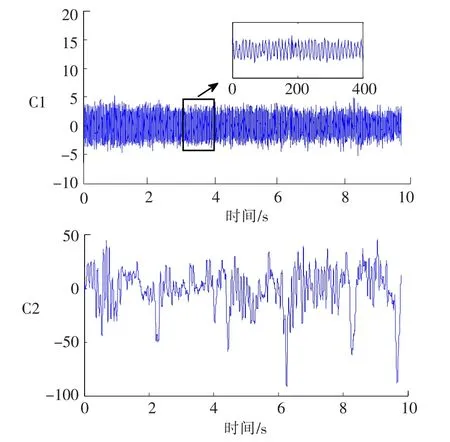
图3 ARMA（3，2）模型估计出的成分Fig.3 Components estimated by ARMA（3，2）model

当增加模型阶数取为ARMA（6，5）时，分解出了更多成分，如图4所示。图4中成分C1为实特征值0.985 7，这是一个接近游走模型的趋势包络成分，主要包含眼电伪迹。成分C2 对应的特征值为0.965 4±0.128 6i，其对应频率为10.54 Hz，这是典型的脑电alpha节律。成分C3 仍是工频干扰。成分C4因其幅值较小，不能当作单独某种成分来分析。

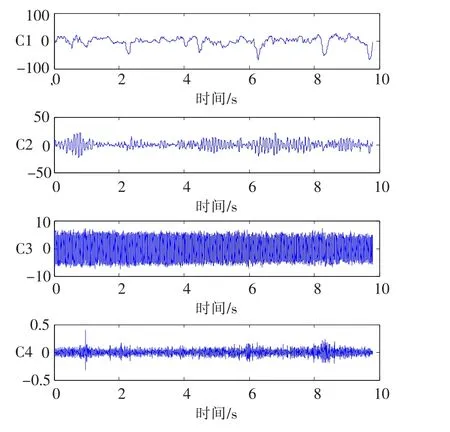
图4 ARMA（6，5）模型估计出的成分Fig.4 Components estimated by ARMA（6，5）model

2.2 多变量序列

对四导脑电分别利用ICA 方法和状态空间方法分解，并对分解结果进行比较。利用独立成分分析对图1中的数据进行成分提取，得到了4种独立成分，如图5所示。它把时间序列分解成独立和不相干的成分，但它只能分解出与变量个数相等的成分数。ICA 方法中Cl成分为眼动伪迹。可见该方法能有效提取眼电伪迹，但其余3种成分并非需要的脑电节律，尤其是其中的alpha节律和工频干扰并没有提取出来。

图5 独立成分分析结果Fig.5 Results of ICA

图6是利用状态空间分解出成分，但与单变量分解不同，这里的成分并非所有导联都相同，它们仅是波形相同，幅值相差一个比例系数。C1仍然是眼动伪迹，C3，C4分别是alpha节律和工频成分。C2也是alpha节律，结果中含有2个alpha节律可能是由于信号平稳性变差、模型阶数较高使得在宽频带范围内分解出2个频点成分。C1～C4为非有效成分，即并不是脑电所具有的信号特征，其他节律成分虽然也含有较大能量，但并没有被分解出来，这主要是由于状态转移矩阵的特征值对应于一个频点而非一个频带造成的，分解出来的成分都是在频谱中表现出尖峰的地方。

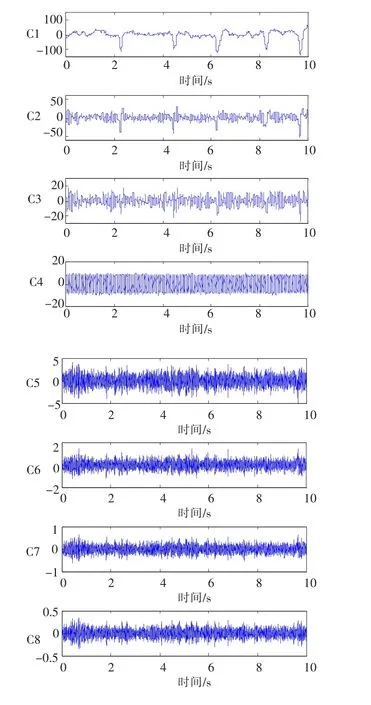
图6 多维数据状态空间估计结果Fig.6 Estimation results by multi－dimension state space method

3 结 语

给出了利用状态空间方法分解时间序列的一般过程，并详述了由ARMA（2，1）和AR（1）描述的结构化状态空间方法。每个ARMA（2，1）子模型表征一个本征频率，AR（1）表征一个包络成分或其他小幅值成分。实现了ARMA（2，1）有效提取节律、工频干扰等频率成分，AR（1）提取眼动伪迹等趋势成分。

通过对单变量和多变量的闭眼静息脑电分析表明，状态空间方法实现了alpha节律、眼动伪迹等的提取，从信号中减去眼动和工频干扰即实现了脑电的去伪迹。在多变量分解实例中，状态空间方法比ICA 分解出更多的有效成分，克服了ICA 方法的限制。

／References：

［1］ XU Jin，LI Wenwen，ZHENG Congxun，et al.Noninvasive detection of brain activity variation under different depth of anesthesia by EEG complexity［J］.Academic Journal of Xi’an Jiaotong University（English Edition），2006，18（1）：36－39.

［2］ BENOIT O，DAURAT A，PRADO J.Slow（0.7～2Hz）and fast（2～4 Hz）delta components are differently correlated to theta，alpha and beta frequency bands during NREM sleep［J］.Clinical Neurophysiology，2000，111（12）：2 103－2 106.

［3］ NIEDERMEYER E.Alpha rhythms as physiological and abnormal phenomena［J］.International Journal of Psychophysiology，1997，26（1／2／3）：31－49.

［4］ MONTEZ T，POIL S S，JONES B F，et al.Altered temporal correlations in parietal alpha and prefrontal theta oscillations in early－stage Alzheimer disease［J］.PNAS，2009，106（5）：1 614－1 619.

［5］ 唐 艳，汤井田.基于独立分量分析的脑电中眼电伪迹消除［J］.计算机工程与应用，2006，23（5）：380－383.TANG Yan，TANG Jingtian.Removal of ocular artifact from EEG based on ICA［J］.Chinese Journal of Medical Physics，2006，23（5）：380－383.

［6］ VIGÁRIO R N.Extraction of ocular artifacts from EEG using independent component analysis［J］.Electroencephalography and Clinical Neurophysiology，1997，13（3）：395－404.

［7］ 李 营，艾玲梅.基于独立分量分析的脑电信号的眼电伪迹消除［J］.计算机工程与应用，2009，45（15）：209－212.LI Ying，AI Lingmei.Removing EOG artifacts from EEG signal based on ICA［J］.Computer Engineering and Applications，2009，45（15）：209－212.

［8］ 韦 明，杨 辉，孙 晓，等.两种去除脑电信号中眼动伪迹的方法比较及其在脑力疲劳测量中的应用［J］.航天医学与医学工程，2012，25（1）：50－53.WEI Ming，YANG Hui，SUN Xiao，et al.Comparison of two for removing EOG artifacts from EEG and appliation in measuring mental fatigue ［J］.Space Medicine ＆ Medical Engineering，2012，25（1）：50－53.

［9］ 邓自立.最优估计理论及其应用——建模、滤波、信息融合估计［M］.哈尔滨：哈尔滨工业大学出版社，2005.DENG Zili.Optimal Estimation Theory with Applications：Modeling，Filtering and Iinformation Fusion Estimation［M］.Harbin：Harbin Institute of Technology Press，2005.

［10］ DURBIN J，KOOPMAN S J.Time Series Analysis by State Space Methods［M］.New York：Oxford University Press，2001.

［11］ 张 兴，杨晓丽.我国能源消费的动态演变——基于时变参数的状态空间模型［J］.河北科技大学学报（社会科学版），2011，11（2）：9－15.ZHANG Xing，YANG Xiaoli.Dynamic evolution of China＇s energy consumption：Based on state space model with time－varying parameters［J］.Journal of Hebei University of Science and Technology（Social Sciences），2011，11（2）：9－15.

［12］ GALKA A，WONG K F K，OZAKI T.Generalized statespace models for modeling nonstationary EEG time－series［J］.Modeling Phase Transitions in the Brain，2010（4）：27－52.

［13］ WONG K F K.Multivariate Time Series Analysis of Heteroscedastic Data with Application to Neuroscience［D］.Kanagawa：Graduate University，2005.