一种新的蛋白质序列二维图形表示方法及应用

张玉岩 闻 佳

（绥化学院 黑龙江绥化 152061）

一、蛋白质序列的二维图形表示方法

当i取值从1到N,这样可以得到点(xi，yi),…(xN，yN)，连接邻接的这些点就可以得到对应的蛋白质图形曲线。

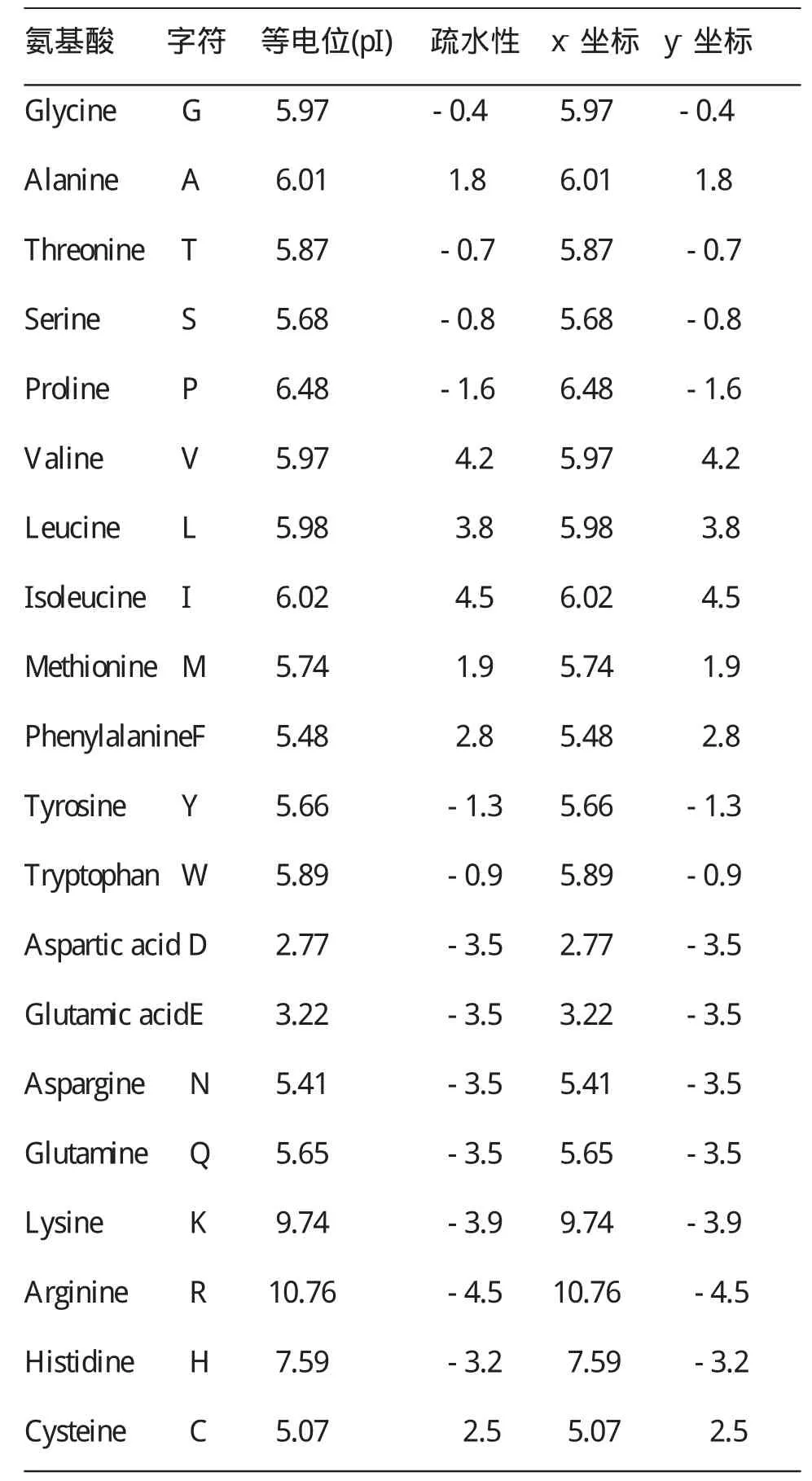
表1 二十种氨基酸对应的数值以及它们在二维直角坐标系中对应的坐标

我们可以证明：我们的模型中的图形曲线不会出现环等简并现象出现，证明过程如下：

假设N表示形成环中对应的氨基酸的个数，每种氨基酸的个数分别用g,a,t,s,p,v,l,i,m,f,y,w,d,e,n,q,k,r,h,和c表示，G,A,T,S,P,V,L,I,M,F,Y,W,D,E,N,Q,K,R,H和C表示每种氨基酸对应的矢量坐标，于是我们可知gG,aA,tT,sS,pP,vV,lL,iI,mM,fF,yY,wW,dD,eE,nN,qQ,kK,rR,hH,和cC形成一个环,因此，上面的环可以表示为：

由于x轴的坐标和可以表示为

于是我们可以解出g=a=t=s=p=v=l=i=m=f=y=w=d=e=n=q=k=r=h=c=0。

因为氨基酸的个数是非负的，所以我们可以确定我们所提出的二维图形中没有环的存在（N>0）。

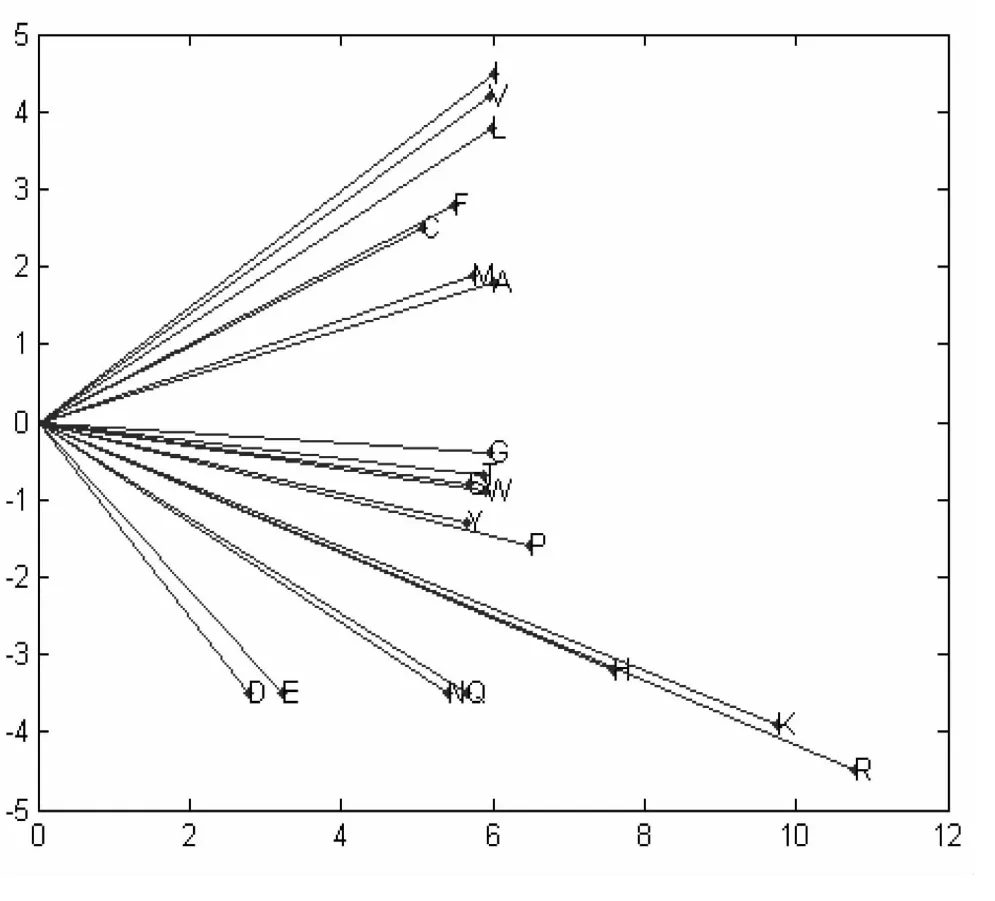
图1.二十种不用的矢量分别表示二十种不同的氨基酸

因为蛋白质的图形曲线和蛋白质序列是一一对应的，所以序列比对可以转化为对应图形曲线的比较。此外，蛋白质序列可以由它所对应的图形进行数值刻画，而且不会丢失任何信息。下面我们通过两条短的蛋白质序列的图形表示来进一步解释我们所提出的方法的有效性。图形2[a(1)]和2[a(2)]是利用我们的所提出方法得到的两条短的蛋白质序列图形曲线。这两条蛋白质序列分别是

通过对比Yu[3]的两个相同的蛋白质序列的图形曲线(图形2[b(1)]和图形2[b(2)]),可以发现，我们的蛋白质图形曲线更直观明显，更容易进行分析和比较。又因为Yu的蛋白质曲线会因为图形曲线的简并现象的存在而更加冗杂，而且对于长的序列是很难进行视觉检测的。

仔细查看图形2,我们还可以发现两条蛋白质序列从整体上看是相似的，这就暗示着它们有几个局部匹配的部分。为了进一步量化两个蛋白质序列的不同，我们把两个蛋白质序列投影在同一个模板中(图形3(a))。因为每一个氨基酸可以用一个独特的矢量来进行数值刻画，所以相同的矢量暗示着相同的氨基酸。在图形3(a)中，我们很容易找到两个蛋白质序列的不相似片段仅出现在位点2,11,14,和27。在图形3(b)中，我们通过考虑对应氨基酸的相对距离用来刻画蛋白质序列比对。在位点2,11,14,和27的相对距离分别是3.5217,4.3484,0.3401,和1.1180。比对对应于氨基酸侧链的酸离解常数的蛋白质序列的图形，我们可以很明显地发现这些不匹配并不都是一样的。比如在位点14，蛋白质I中的Valine被替换为蛋白质II中的Isoleucine，这里的不匹配伴随着一个小的相对距离。通过比较我们还会发现，两个属于相同类别的氨基酸相对于属于不同类别的氨基酸更很容易发生替换。在这两个蛋白质之间一共有四个不匹配，其中对应于小振幅的相对距离更不容易改变蛋白质的内在属性。

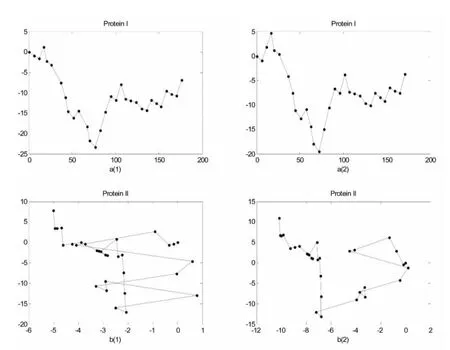
图2.蛋白质I和蛋白质II的二维图形表示

图3.蛋白质序列I和蛋白质序列II的图形比对

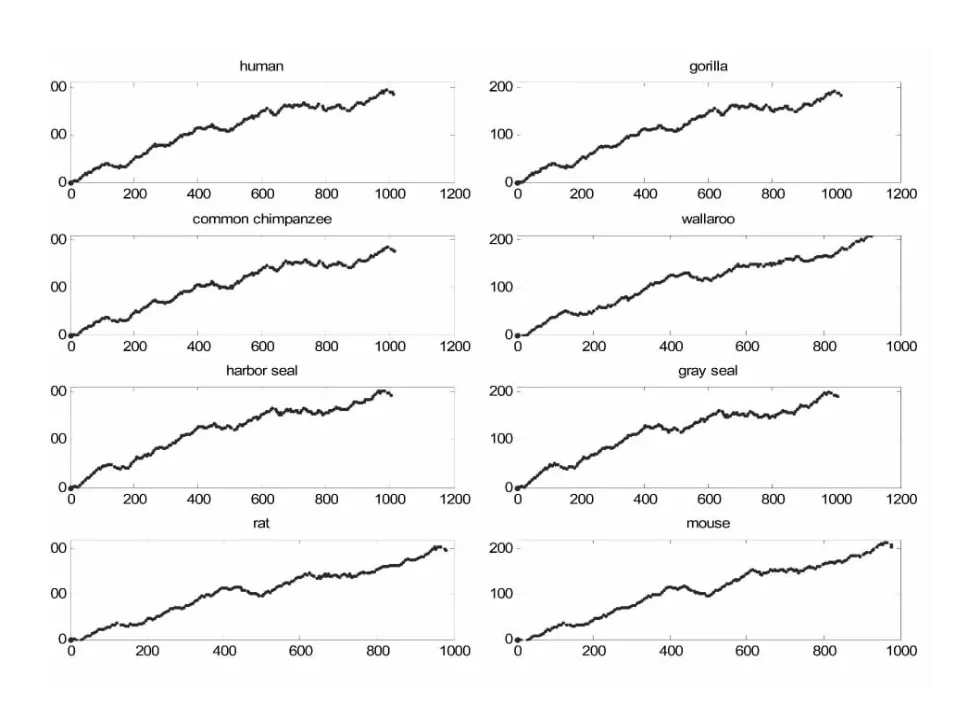
图4.八种ND6蛋白质序列的二维图形表示

在图形4中，我们给出了八种ND6蛋白质序列所对应的二维图形曲线表示。通过比较这些图形曲线，我们会能够发现人、大猩猩和黑猩猩（human,gorilla,common chimpanzee）在整体上是更为相似的，同时麻斑海豹和灰海豹（harbor seal-gray seal），大鼠和小鼠（rat-mouse）也是很相似的。此外，大袋鼠（wallaroo）明显地区别于其他物种。这些结论和已知的生物进化结论和其他已出版文献的结论是完全一样的[4-6]。

[1]Yao,Y.H.;Dai,Q.;Li,L.;Nan,X..Y.;He,P.A.;Zhang,Y.Z.JComput Chem 2010,31,1045-1452.

[2]Wen,J.;Zhang,Y.Y.Chem Phys Lett 2009,476,281-286.

[3]Yu,J.F.;Sun,X.;Wang,J.H.J Inter J Quan Chem 2011,111,2835-2843.

[4]Li,M.;Badger,J.H.;Chen,X.;Kwong,S.;Kearney,P.;Zhang,H.Bioinformatics 2001,17,149-154.

[5]Out,H.H.;Sayood,K.Bioinformatics 2003,19,2122-2130.

[6]Makarenkov,V.;Lapointe,F.Bioinformatics 2004,20,2113-2121.