基于ANSYS的飞机轮胎分解机效果分析

解本铭，张敏健

（中国民航大学机场学院，天津 300300）

轮胎是飞机的重要部件，由于飞机轮胎磨损快，轮胎与轮辋经充气且长时间使用后会粘结在一起，加上轮胎重量较重，更换时需专用设备分解与装配，如图1所示。目前中国急需研制性价比高的机轮拆装设备，以装备各航空公司的维修基地[1]。针对目前使用较多的拆胎机的压盘结构模拟了轮胎分解过程，以期对新型飞机轮胎分解机的设计提供计算依据。

图1 一种飞机轮胎分解机Fig.1 Plane tyre dismounting machine

轮胎是由胎冠、胎侧、帘布、钢丝圈等组成的结构体，其力学特性涉及到材料非线性、几何非线性及轮胎与压盘之间的接触非线性等复杂问题。对子午线飞机轮胎进行数学分析极其困难，许多性能分析方法也只是近似的定性分析，目前文献中对飞机轮胎的研究比较少。分解机是通过压胎辊子的挤压旋转使轮胎的轮辋与轮毂彻底分离。本文通过PRO/E对B737系列的H40×14.5-19轮胎进行了三维建模，也对相对应的轮辋、压盘进行了三维建模，通过接口程序导入有限元软件ANSYS中，建立有限元模型开展相关分析。

1 飞机轮胎的非线性特性及有限元分析方法

1.1 无气轮胎的材料非线性

轮胎分解机对轮胎进行压胎分解是在轮胎无气状态下进行的。无论是橡胶还是橡胶帘线复合材料，轮胎的材料具有典型的非线性特征[2]。轮胎分解过程具有典型的大变形特征，如果用传统的线弹性小应变理论进行分析研究，其结果必然会产生很大误差。

橡胶材料为超弹性材料，其力学特性可用应变能密度函数来描述，如Rivlin模型等。目前最常用的Neo-Hookean模型与Mooney-Rivilin模型就是Rivlin模型的简化形式之一[3]。Rivlin模型为

式中：W为材料应变能；Cij为材料常数；I1、I2为第1、第2应变不变量，即

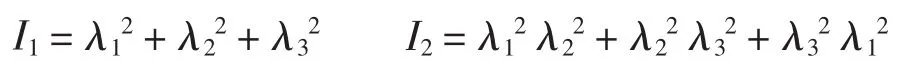
式中：λ1、λ2、λ3为三个拉伸方向的伸长率=1。

Mooney-Rivlin方程要求剪切应力-应变关系呈线性，但Yeoh方程表明炭黑填充材料的情况并非如此。Yeoh根据炭黑填充橡胶材料的实验数据给出远远小于（接近于0，且不等于0），若采用不变量（I1-3）作为应变能密度W的一种三次方程，能很好地描述橡胶材料的弹性力学性能，适用于轮胎橡胶材料的非线性有限元分析[4]

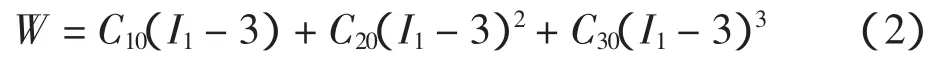
式中：W 为材料应变能；C10、C20、C30为 Rivlin 系数，可由单轴拉伸试验来确定，见文献[5]。

1.2 无气轮胎的几何非线性

几何非线性是由飞机轮胎的大变形引起的，可采用Total Lagrange法[6]，经转换可得最终矩阵形式为

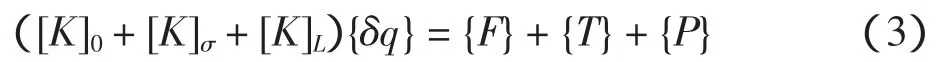
式中：[K]0为切线刚度矩阵，表征载荷增量与位移的关系；[K]σ为初应力刚度矩阵，表征在大应变情况下初应力对结构的影响；[K]L为初位移刚度矩阵，表征大位移引起的结构刚度变化；{δq}为节点坐标增量矢量；{F}为体载荷矢量；{T}为面载荷矢量；{P}为应力在节点上的等价合力矢量。式（3）即为Total Lagrange法的有限元方程。

1.3 状态非线性（接触非线性）

接触问题是一种普遍的状态非线性行为，具有高度非线性特点。在轮胎分解过程中主要存在两个接触问题：轮胎与轮辋的接触、轮胎与压盘的接触。此处主要研究不同压盘形状轮胎分解效果。为了更好地观察轮胎的变形，可假定轮辋与压盘都为刚体，利用ANSYS的刚体—柔体接触进行有限元分析。

根据拉格朗日乘子法与罚函数法构成的混合法原理[6]，由变分原理可知，系统的总势能为

式中：E为系统的内力势能；Q为接触力势能；W为系统的外力势能。

式中：C为接触边界条件；{F}为接触力向量，{F}={Ft，Fn}T，t和n分别表示切向和法向；{g}为接触间隙向量，{g}={gt，gn}T；a*为罚函数因子。

随着接触状态的变化，将式（4）取变分及驻值

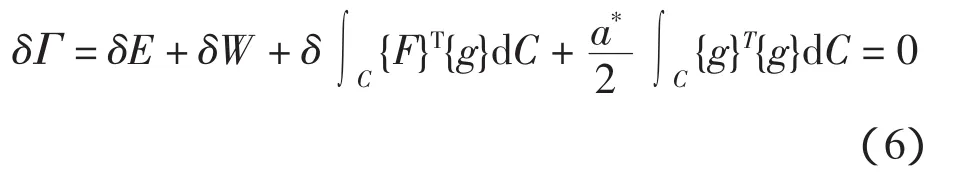
接触体离散化后，可由式（6）导出以各节点位移和接触力为未知量的有限元平衡方程。增强的拉格朗日乘子法结合了拉格朗日乘子法与反函数法的优点，分析采用此方法。

2 分解机压胎过程模拟有限元分析

2.1 轮胎三维模型的建立

轮胎有限元分析的难点和关键技术之一就是轮胎结构与构型的精确模拟。根据橡胶工业手册第四分册[7]与实验室现有轮胎实物，如图2所示，结合文献[8]子午线轮胎结构设计与制造技术确定该轮胎断面轮廓参数。为了能在ANSYS中更好地表达轮胎各个不同层的材料属性，通过装配体来建立轮胎的整体模型。利用轮胎的对称性，主要取轮胎的1/4模型的半侧进行分析。在PRO/E中建立装配体模型，通过专门的接口程序转换到ANSYS中，如图3所示。

2.2 轮胎的材料模型

子午线轮胎的结构非常复杂，主要由胎冠、帘布层、胎体层、胎侧、钢丝圈等部分组成。此处主要建立了9种材料模型，如图4所示。胎肩、胎侧、内衬层、三角胶、包布层为纯橡胶材料；胎冠层、胎体层为复合材料；帘布层与钢丝圈为线性材料。橡胶材料为超弹性材料，除非在小应变范围内，一般不定义杨氏模量E。

[9]，输入以下材料属性，如表1所示。

2.3 有限元单元的生成

图2 米其林H40×14.5-19轮胎Fig.2 Michelin H40×14.5-19 tyre

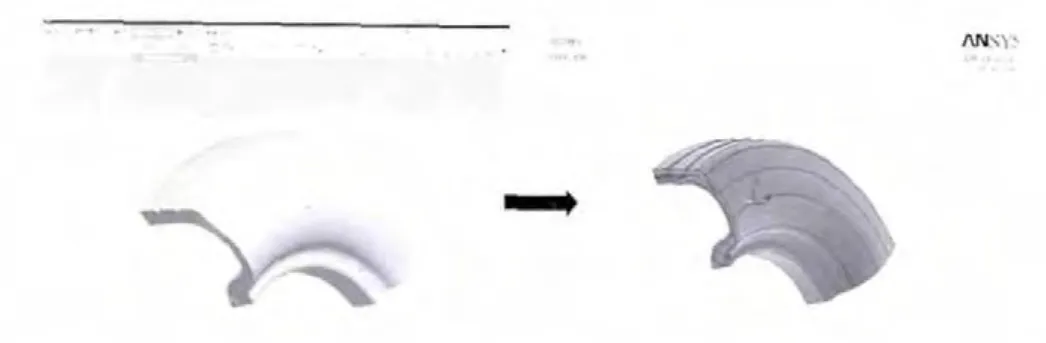
图3 PRO/E轮胎模型导入ANSYS中Fig.3 Move PRO/E tyre model to ANSYS

图4 H40×14.5-19轮胎断面轮廓及材料分布图Fig.4 H40×14.5-19 tyre’s cross-section and material distribution

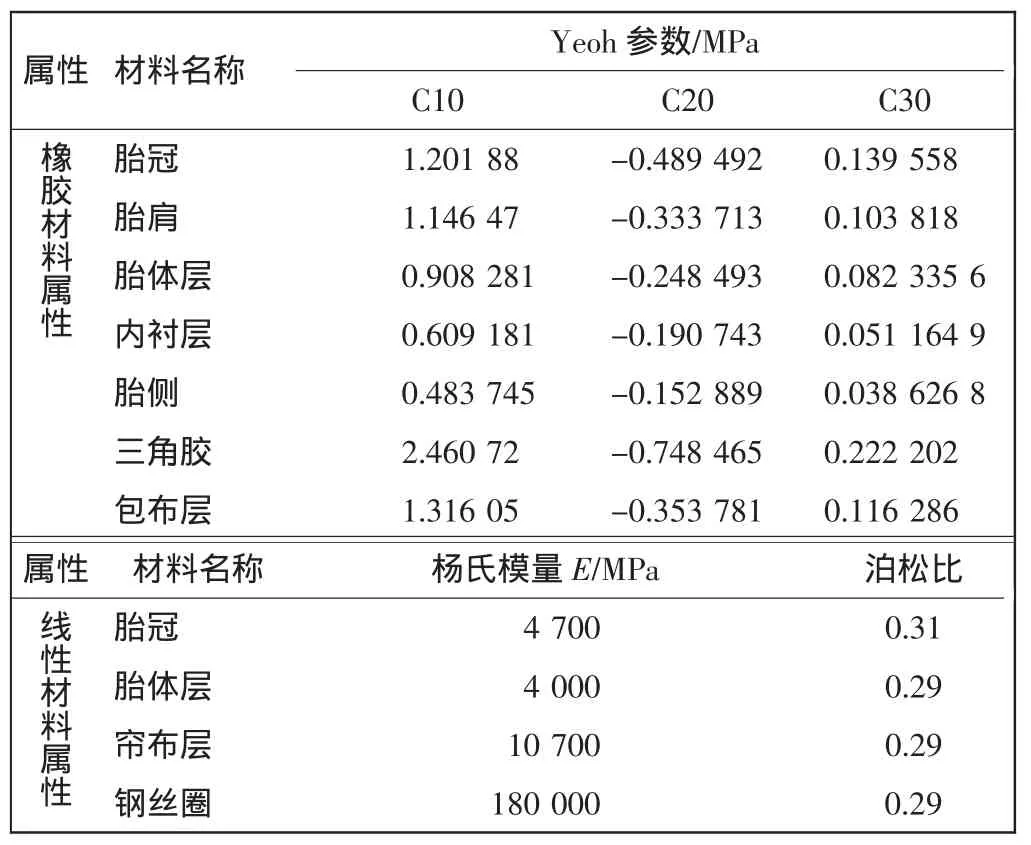
表1 子午线轮胎材料属性Tab.1 Material property of radial tyre

研究采用SOLID185单元、sweep方式进行网格划分，线单元长度为0.02 mm，本模型共生成节点8 160个，单元6 903个。网格划分结果如图5所示。

图5 90°H40×14.5-19轮胎有限元模型Fig.5 H40×14.5-19 tyre’s finite element model

2.4 轮辋与压盘模型的建立

由于主要研究在压盘的压力下轮胎的变形，故可将轮辋与压盘作为刚体，轮辋根据文献[4]进行绘制，只需准确建立与轮胎接触部分的模型即可；轮辋建立95°模型。压胎圆盘取大径为580 mm，厚度为60 mm，建立90°模型。导入ANSYS中，如图6所示。

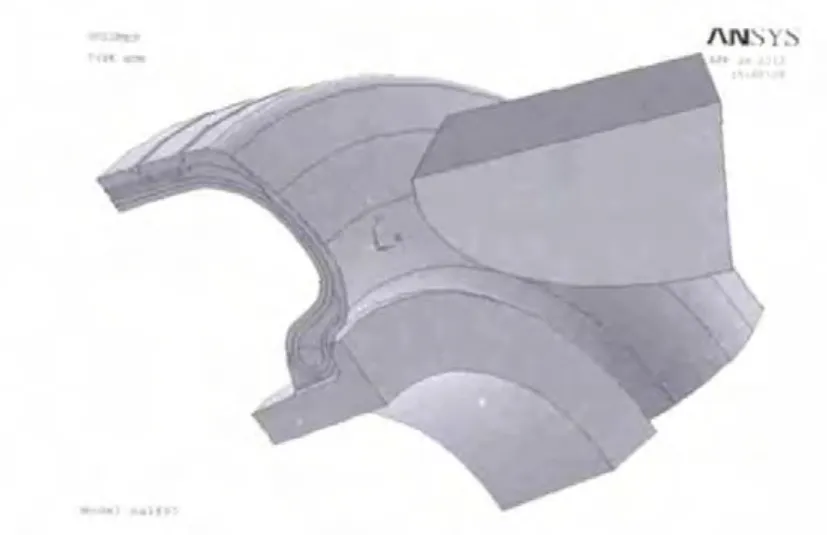
图6 加入轮辋与压盘的模型Fig.6 Model with rim and disk

2.5 接触对的创建

轮辋与轮胎、压盘与轮胎都采用面-面接触分析，轮辋与压盘为刚体选为目标单元，采用TARGE170单元；轮胎选为接触单元，采用CONTA174单元。

轮胎与轮辋的接触对如图7所示。轮胎在进行分解时是在无气状态下进行的，故不存在过盈配合的情况。轮胎与轮辋的接触采用标准的库伦摩擦模型。飞机轮胎充气状态下长期使用后轮胎与轮辋会粘结在一起，压胎过程受此粘结阻力的影响很大。接触对的实常数COHE为滑动粘滞阻力，可通过设置此常数来真实的模拟压胎过程，设COHE为0.1 MPa。

图7 轮辋与轮胎的接触对Fig.7 Contact pair of rim and tire

轮胎与压盘的接触对如图8所示。该接触也采用标准的库伦摩擦模型。为了模拟压盘的压胎过程，选取了刚性体压盘上的一个点作为pilot节点，pilot节点的自由度代表着整个刚性目标面的运动，它是只有一个节点的单元，可以把pilot节点作为刚性目标面的控制器。pilot节点可以是目标单元上的任何一个节点，可以位于任何位置，但是它不能是接触单元上的节点。

图8 轮胎与压盘的接触对Fig.8 Contact pair of disk and tyre

2.6 施加约束与设置分析选项

建立以轮胎旋转中心为原点的柱坐标系，对轮胎的对称面施加对称约束，且将对称面上的所有节点转换到柱坐标系中，施加θ方向与Z方向约束。

对接触对中的pilot节点施加位移约束：UX=50 mm，UY=18.2 mm。

将两个接触单元的接触算法都设置为扩展的拉格朗日法。

在分析选项设置中，设置分析类型为large displacement static；打开自动时间步长，设置载荷步为25，最大子步数为1 000，最小为5；打开牛顿-拉普森选项，并设置为full，以加快收敛。

2.7 不同形状的压盘压胎过程有限元分析

轮胎分解机分解轮胎时的简化模型如图9所示，在角α、杆长L、压胎盘大径D不变的情况下，主要对β 角分别为 20°、30°、40°、45°时三种不同形状的压盘分解轮胎进行了分析模拟。

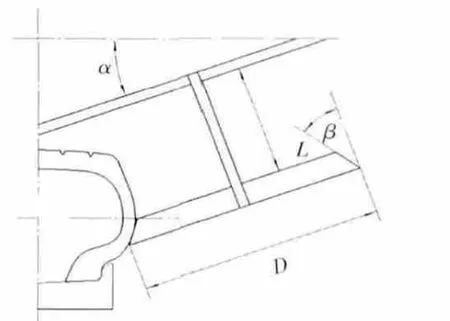
图9 轮胎分解机分解轮胎时的简化模型Fig.9 Simplified model of decomposing tyre in machine

3 计算结果及分析

β角为20°时的迭代求解收敛过程图如图10所示，β 角分别为 20°、30°、40°、45°时轮胎 X 方向位移图，如图11～图14所示。

图10 β角为20°时的迭代求解收敛过程Fig.10 Convergence process of iterate resolving when β is 20°

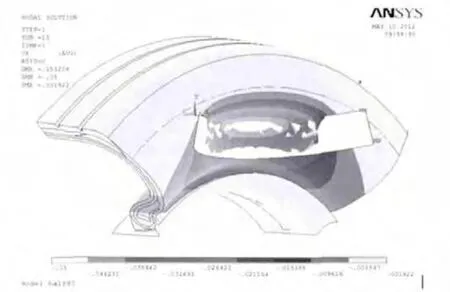
图11 β角为20°时的X方向节点位移图Fig.11 Modal displacement in X-direction when β is 20°

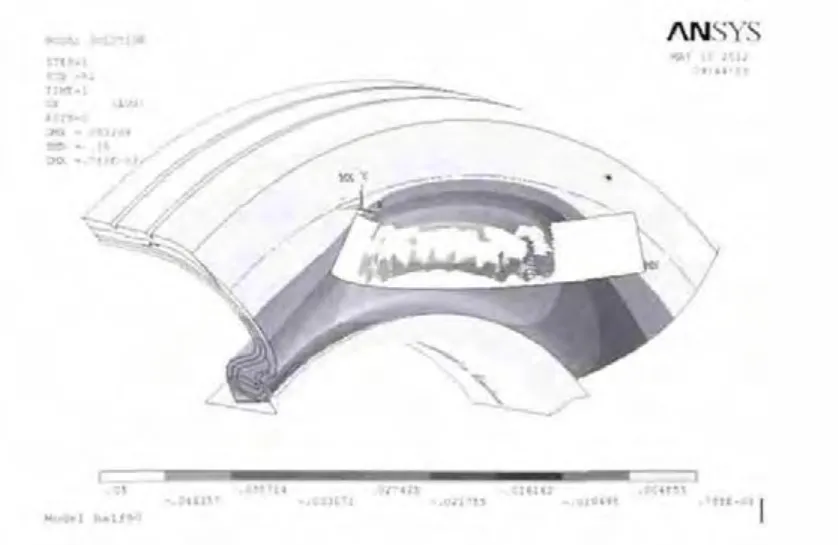
图12 β角为30°时X方向节点位移图Fig.12 Nodal displacement in X-direction when β is 30°

由图11～图14可以看出，当β角为20°时，与轮辋接触面上的节点只有一部分节点有位移变化；而当β角变为30°时，位移变形明显增大，与轮辋接触面上的节点变形区域明显增多；当β角为40°时，相对于30°时变形近一步加大；当β角为45°时，虽然轮胎整体的变形区域变大，但可看出变形大小相对于40°较小。

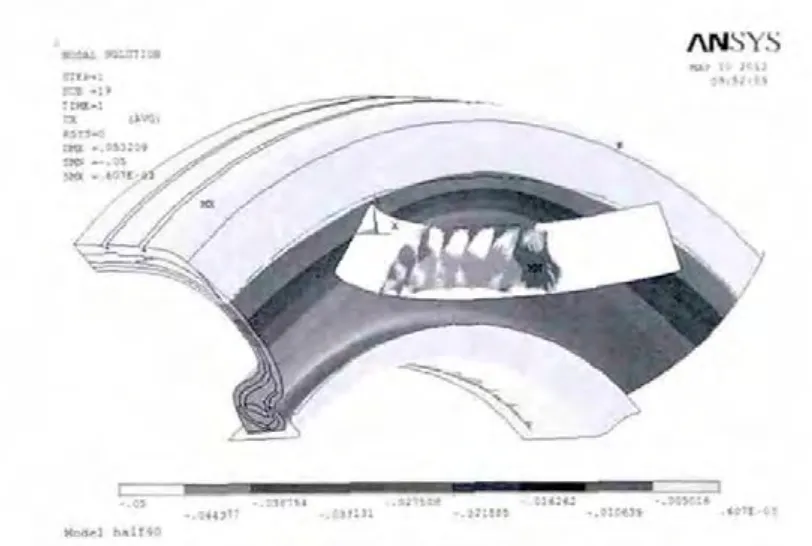
图13 β角为40°时X方向节点位移图Fig.13 Nodal displacement in X-direction when β is 40°

图14 β角为45°时X方向节点位移图Fig.14 Nodal displacement in X-direction when β is 45°

为了能更好地看出轮胎分解的效果，列出了轮胎与轮辋接触面上与压胎盘中心线最近的4个节点的X方向位移，如表2所示。

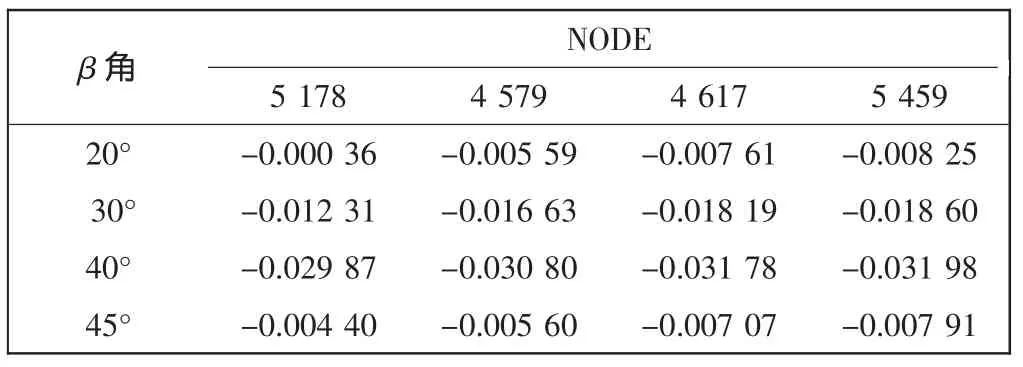
表2 选取节点的X方向的位移Tab.2 Selected nodes’displacement in X-direction

经验证相同的节点号在不同的图形中对应在轮胎上的位置完全相同，可用于对比分析。从轮胎内侧到外侧节点号依次为：5 178、4 579、4 617、5 459。

由表2可看出，同一种形状的压盘分解轮胎时，轮胎与轮辋接触面上最外侧节点位移最大，最内侧最小，且呈递减趋势，与实际情况相符合。当压胎盘β角从20°变为30°，再到40°时，选取的4个节点位移逐渐增大。当角为45°时，4个节点的位移变形又减小。

由以上分析可知，当压胎盘β角为40°时，轮胎变形最大，与轮辋接触面的节点变形最大，轮胎分解效果最好。

4 结语

通过查阅资料与利用实物测量，利用PRO/E装配体建立了多种材料组成的几何形状复杂的飞机子午线轮胎H40×14.5-19的三维模型，建立了轮辋和三种不同形状的压盘的简化模型，并通过接口程序导入有限元软件ANSYS中，建立了有限元模型；建立了轮胎轮辋、轮胎压盘的接触单元，并通过pilot节点法模拟了压盘分解轮胎过程，分析时充分考虑了轮胎材料的材料非线性、几何非线性和接触非线性，且为了更真实地模拟其分解过程，通过查阅相关资料赋予了轮胎与轮辋的一定的初始结合力。分析了在给压盘相同位移时，轮胎在不同形状的压盘挤压下的变形，结果表明当β角为40°时，轮胎分解效果好，位移变化大。分析结果还可为轮胎分解机其它结构的设计提供理论依据。该轮胎有限元模型还可用于压胎盘的更进一步研究，也可有效地用于以后的飞机轮胎研究分析中。

参考文献：

[1]王立文，高建树，赵 炜.液压式飞机轮胎分解/装配机[J].液压气动与密封，2003（4）：32-34.

[2]李 莉，胡立臣，邵朋礼.无气轮胎几何非线性的有限元分析[J].机械设计，2008，25（8）：10-12.

[3]刘 峰，李丽娟，杨学贵.轮胎与地面接触问题的非线性有限元分析[J].应用力学学报，2011，18（4）：141-146.

[4]王 伟，徐忠丽，邓 涛，等.载重子午线轮胎接地面有限元分析[J].弹性体，2006，16（1）：29-32.

[5]OH YEOH.Characterization of elastic properties of carbon black filled rubber vulcanization[J].Rubber Chemical and Technology，1990，63（5）：792-805.

[6]崔玉福，郑慕侨.负重轮实心橡胶轮胎滚动状态下接触三维有限元分析[J].轮胎工业，1998，18（5）：275-280.

[7]梁守智，钟延壎，张丹秋.橡胶工业手册（第四分册）[M].北京：化学工业出版社，1993.

[8]俞 淇，丁剑平，等.子午线轮胎结构设计与制造技术[M].北京：化学工业出版社，2006.

[9]应卓凡.子午线轮胎的刚度特性和制动摩擦力的三维有限元分析[D].广州：华南理工大学，2010.