基于遗传算法的动平衡优化方法研究

瞿红春，崔秀峰

（中国民航大学航空工程学院，天津 300300）

1996年初至1999年8月，V2500发动机营运过程中发生的一些典型故障及其占发动机故障的百分比显示ATA77章所对应的发动机系统故障率最高，而发动机N1振动占ATA77章故障的47.48%，占发动机故障的11.8%，具有较高的故障发生率。发动机N1振动产生的原因主要是N1转子的动不平衡引起，所以研究一种有效的N1转子动平衡方法以减少启车次数，可极大地减少发动机动平衡的成本。

转子系统分为刚性转子和柔性转子，N1转子就属于柔性转子。柔性转子动平衡的方法可归纳为振型分离法与影响系数法两大类。振型分离法要求操作者具有较丰富的经验和知识，不容易配备计算机辅助。影响系数法的实质是矢量平衡法的发展，其优点完全凭借试验进行，两个振型或更多振型同时进行平衡，可采用计算机辅助和自动化。1994年，Austrow提出了对于燃气涡轮发动机平衡的优化平衡重量探索法，它影响了系数平衡法的发展。这种方法使用了一些测定的或事先已知的影响系数以及测定的振动数据，以决定优化的平衡校正重量。目前的航空发动机转子平衡方法都是基于影响系数法矩阵，通过做影响系数法实验来求得，这样会使航空发动机进行多次试重启车，进而加大平衡的费用和时间。

研究了无试重动平衡法[1]，基于全息谱技术[2]，从影响系数法[3]的本质出发，采用最小二乘法的求解思想，以使转子残余振动量最小为目标，通过应用遗传算法[4]求得一组平衡配重值，使发动机N1转子在其额定工作转速范围内，N1转子产生的振动与转子的原始振动不平衡响应相抵消，从而保证转子的振动值达到手册标准要求，达到无试重启车[5]的目的。

1 优化动平衡方法的实现

柔性转子的平衡是在下面两个线性条件下进行的。在一定平衡条件下：①轴承的振幅与转子同一点处的不平衡量大小成正比；②轴承振幅与不平衡力之间的相位角不变。通过全息谱分析和不平衡相应的计算，可得不同转速下不平衡初相点的一个解集，然后再用遗传算法对这些解进行优化搜索，使其达到最小二乘法思想的“残余振动最小”的目的。

1.1 遗传算法原理

遗传算法是由J.H.Holland提出的一种模拟生物进化过程中自然选择机制的优化方法，如图1所示。

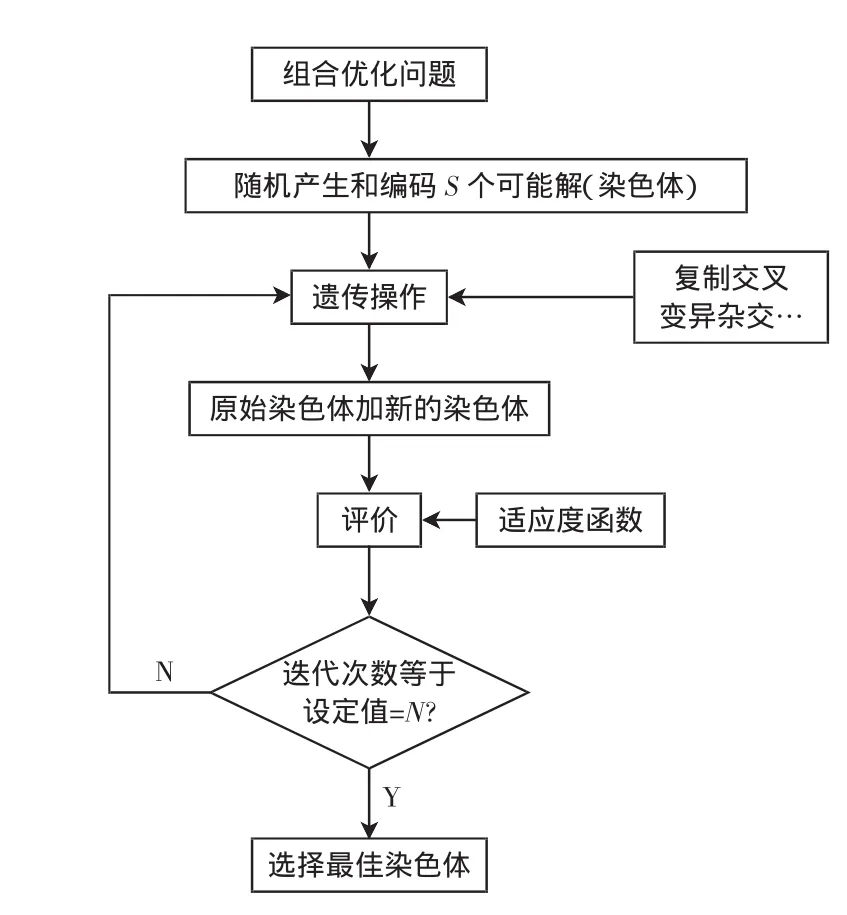
图1 遗传算法原理图Fig.1 Genetic algorithm flow chart

1.2遗传算法的实现步骤

1.2.1 确定编码方式

遗传算法不能直接处理问题空间的参数，必须把它们转换成由一定结构组成的染色体或个体。设x为二进制编码染色体串，如果x的第i位为1，则表示该特征被选中；如果为0，则表示该特征未被选中，其中，x的位数为总的特征数。编码前必须确定参数的范围，包括平衡转速范围内的平衡刚度系数和平均阻尼系数。

1.2.2 群体初始化

遗传算法是对多个个体同时进行处理，这些个体组成了群体，群体初始化就是产生进化的起点群体。初始化前，要确定群体规模，它影响遗传优化的最终结果以及遗传算法的执行效率。在实际应用中，群体规模的取值范围一般为几十到几百。

1.2.3 确定优化函数

设实测的N1转子原始的振动量为A，利用最小二乘法的优化思想，定义其中由平衡配重引起的单独纯振动量V（uk），而N1转子的振动量用全息谱初相点来表示，并且定义残余振动向量为

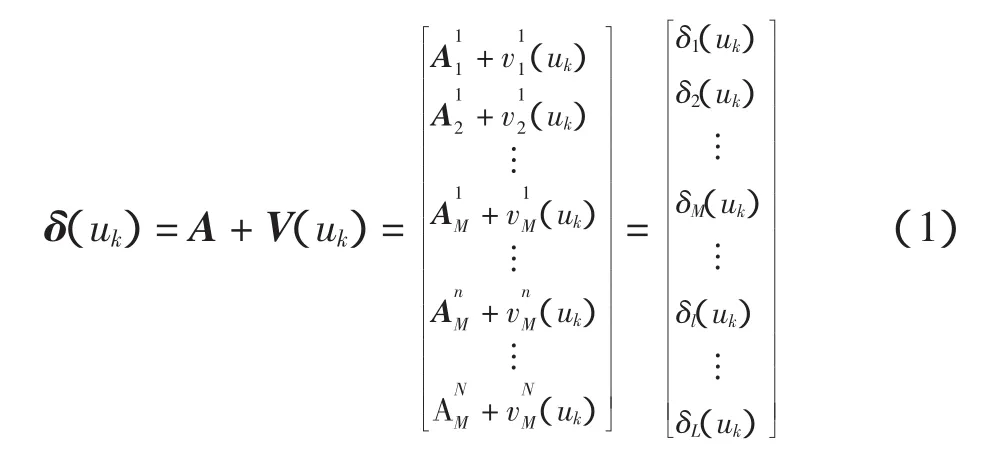
根据影响系数平衡法的最小二乘思想，优化函数定义为：

N1转子残余振动分量的平方和最小化

最大残余振动分量的模最小化

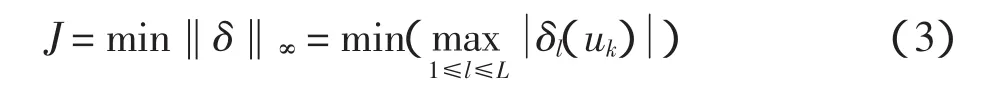
优化目标式（2）、式（3）的约束条件为

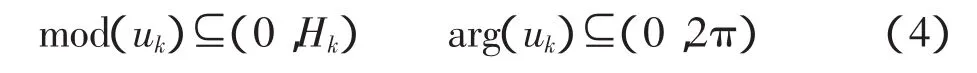
式中：mod表示相应的模；arg表示相应的相位角；Hk表示相应的第k个平衡面上所加平衡配重的最大值。

1.3 优化搜索的实现

有了编码和优化目标函数，就能利用遗传算法进行优化搜索。航空发动机转子动平衡的配重优化搜索是一个解集的优化搜索问题，目前有很多智能优化算法，如人工神经网络、专家系统和遗传算法等。本文之所以用遗传算法作为优化算法，是由于它在实现此类问题的优化过程中具有以下特点：

1）遗传算法不直接对参数本身进行处理，而是对编码后的个体进行处理。

2）不同于传统的单点搜索算法，遗传算法同时对群体中的多个体进行处理。对于多峰问题，有良好的全局搜索能力，减小了局部最优的风险。

3）遗传算法的适应度函数，不受连续可微等条件限制，定义域可任意设定，因此遗传算法的适用面更广，尤其适合于处理复杂的非线性问题。

本文采用Matlab遗传算法工具箱进行遗传算法编程及优化搜索。

2 动平衡实验

实验台如图2所示，其中已知发动机转子系统的第一、二阶临界转速分别为1949 r/min（实测约为2000 r/min）、4018 r/min。利用传递矩阵法计算转子的不平衡响应，采用双面平衡法进行动平衡。采用遗传算法来优化搜索，优化目标函数取为式（2）、式（4）。此实验台N1转子平衡面的最大配重不超过3 g，因此取Hk=3 g，k=1，2。取转子在平衡转速范围内的平衡刚度系数K=5.21×105N/m及平均阻尼系数C=18.47 kg/s，初始群体个数选为80个，进化截止代数为20代，测量发动机N1转子的原始振动量，如图3所示。选取 5 个平衡转速：1000、2300、3000、3600、4200 r/min，（如图 4中的“○”所示）。

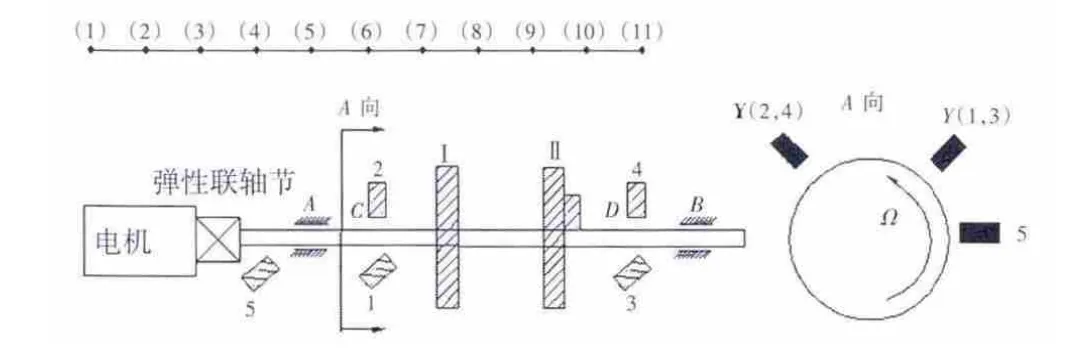
图2 实验台转子结构示意图Fig.2 Schematic diagram of rotor structure

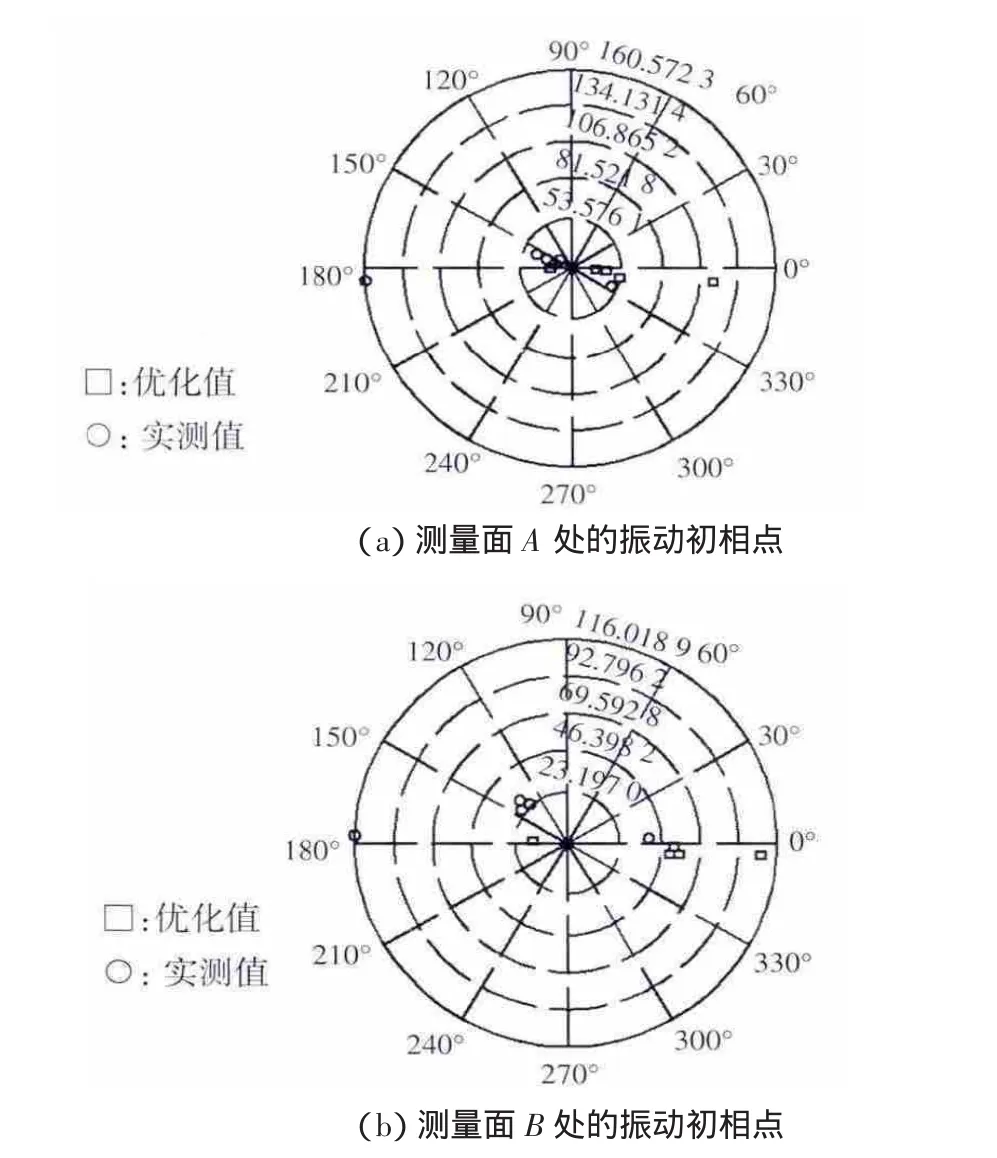
图3 在各个平衡转速下N1转子优化配重前后振动产生的初相点分布Fig.3 Original phase point distribution under five balance rotational speeds before and after optimization

观察可以确定，两种响应相互抵消，实验结果较为理想.计算所得的配重值如表1所示。

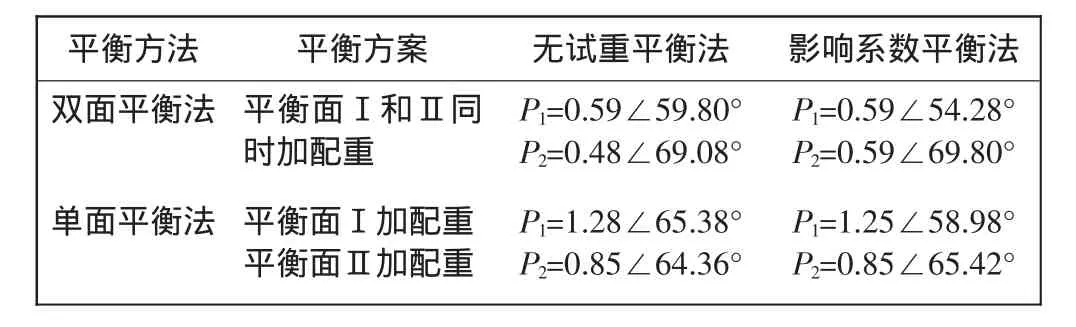
表1 实验所得转子的平衡配重值Tab.1 Balance weight of rotor by experiment

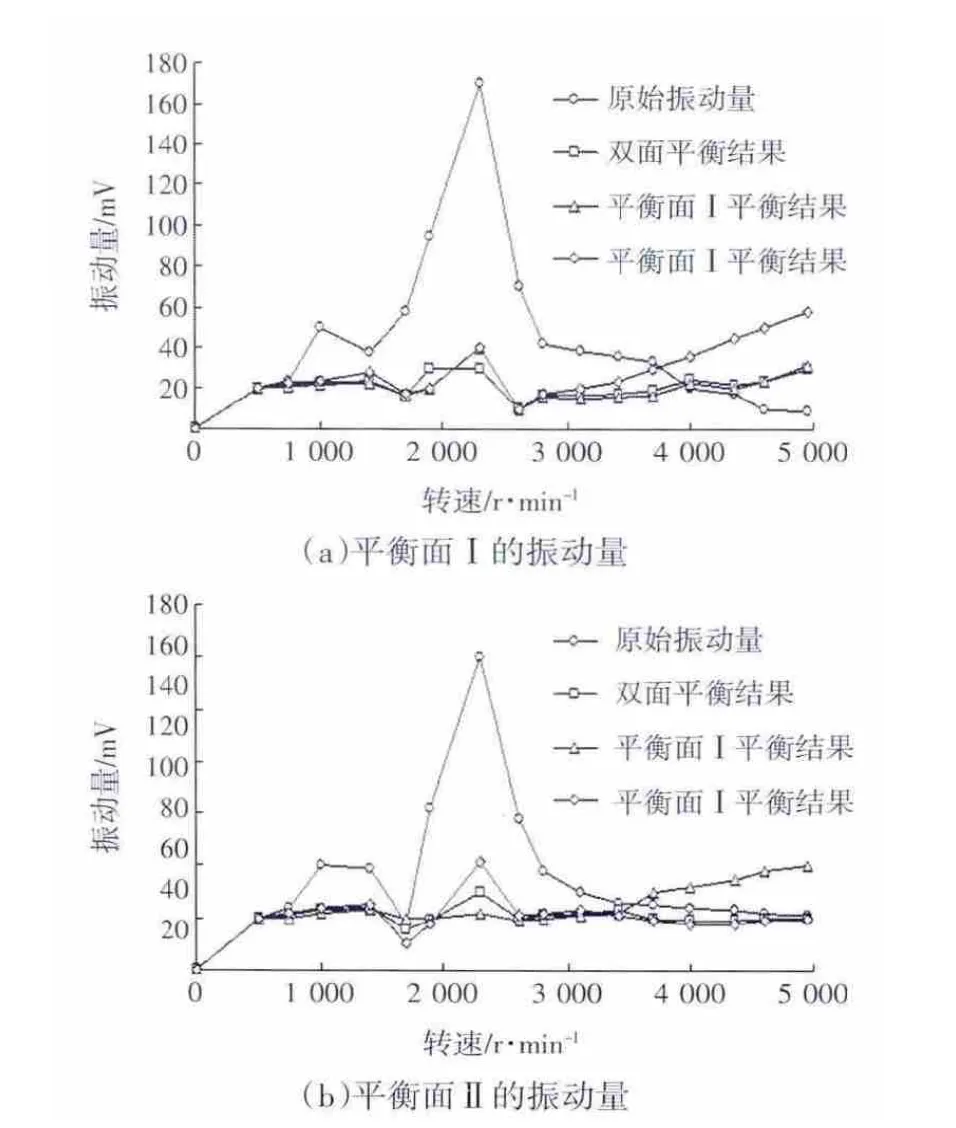
图4 不同启车过程中测量面的振动量Fig.4 Vibration of measurement plane under different start processes

3 结语

基于遗传算法的动平衡优化方法以虚拟配重代替现场平衡过程中的试重启车，无需多次启车试重即可计算出不平衡量的分布，提高了平衡的效率。通过不平衡响应和全息谱分析详细计算配重的大小以及相位，提高了平衡的精度。遗传优化算法用计算机作为辅助，计算出平衡配重量，大大提高了计算速度。因此，遗传优化算法是一种很有应用前景的发动机动平衡方法。

[1]MORTON P G.Modal balancing of flexible shafts without trial weights[J].Proceedings of the Institution of Mechanical Engineers，1985，199（C1）：71-78.

[2]屈梁生.机械故障的全息诊断原理[M].北京：科学出版社，2007：145-166.

[3]AUSTROWJ C.Source：Optimum balance weight search algorithm[J].Journal of Engineering for Gas Turbines and Power，Transactions of the ASME，1994，116（3）：678-681.

[4]屈梁生，张西宁.沈玉娣机械故障诊断理论与方法[M].西安：西安交通大学出版社，2009：114-131.

[5]GNIELKA P.Modal balancing of flexible rotors without test runs：an experimental investigation[J].Journal of Sound and Vibration，1983，90（2）：157-172.