基于FPGA的正交匹配追踪算法的硬件实现

熊承义，董攀峰

(中南民族大学电子信息工程学院，武汉430074)

新近发展的压缩感知(CS)理论［1，2］指出，当信号是时域稀疏的或在某个线性变换域内稀疏时，可利用与系数变换基不相干的观测矩阵，将对应的稀疏信号投影到观测矩阵中以获得低维观测向量.观测向量中保留了原信号足够的信息量，通过求解一个优化模型可以高概率地重构原信号.在CS理论框架下，信号的采样速率不再由带宽决定，而仅取决于信号的稀疏性以及变换基与观测矩阵的不相关性.

目前该领域还有很多问题需要研究，重构算法是其中一个极其重要的研究方向.在基于FPGA的OMP算法的VLSI设计方面，文献［3］提出了一种动态流水线结构，并采用资源复用技术，大大体提高了资源利用率.文献［4］通过优化OMP算法，能够大幅度的消减计算延时.通过对该算法的理论分析，本文研究了一种基于FPGA的OMP算法的硬件实现，仿真结果验证了所设计的硬体结构可以较好地重建原信号.

1 OMP算法

1.1 算法原理

在CS中，采样过程是由稀疏度为k的原信号x∈RN和测量矩阵 Ф∈RM×N相乘，其列表示 φ1，…，φN，得到测量向量y∈RM，其长度远小于原信号x.OMP算法需要两个输入，测量矩阵Ф和测量向量y，最后得到稀疏度为k的原信号的估计.残差在OMP算法中是一个重要的度量量，对残差信号r的控制体现了匹配追踪算法的核心思想.在每次迭代过程中，选出测量矩阵Φ与残差r最匹配的原子，然后通过消除该原子的贡献来计算新的残差，并得到一个新的估计，经过k次迭代，该算法将计算出原信号的估计.以下为OMP重建的过程.

(1)初始化残差r0=y，索引集Λ={Φ}，迭代索引i=1.

(2)寻找测量矩阵Φ中与残差最匹配的原子:

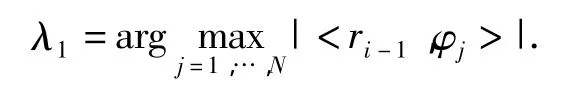
(3)增加支撑集Λj=Λj-1∪{λi}，并增广矩阵 ~Ψi=

(4)利用索引集中现有的原子逼近原始信号:

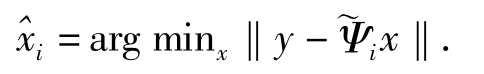
(5)更新残差信号:

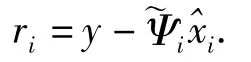
(6)迭代索引加1，如果i＜k返回到第(2)步得到最后的近似信号.

1.2 计算步骤

OMP算法一次迭代过程可以分为3个模块.第一个模块对应于重建过程的第(2)和(3)步，寻找最匹配的原子.这个步骤涉及矩阵和向量的乘法，一次迭代就需要N×M次标准矩阵向量操作的乘法.经过原子选择，输出的是测量矩阵Φ中与残差最匹配的原子.

第二个模块对应的是第(4)步，求解L0范数最小模型，得到原信号的估计.通过求扩充矩阵~Ψ的逆，可以求解方程y=~Ψ×，从而得到原始信号的估计.但是，矩阵~Ψ不是方形矩阵.对于非方形矩阵求逆，常见的处理办法方法是使用反Moore-Penrose伪逆，它可表示为:

进而可以得到原始信号的估计，如下:

其中令:

这个模块涉及矩阵乘法和矩阵求逆.若直接进行矩阵的求逆，是不易于FPGA实现的，可以通过先分解然后分别求逆.矩阵分解算法主要包括QR分解、奇异值分解、LU分解以及Cholesky分解，其中比较常见的是QR分解和LU分解.QR分解是利用一个正交相似变换将给定的矩阵逐步约化为上三角矩阵或拟上三角矩阵.QR分解和奇异值分解过程复杂并且计算复杂度高，在FPGA上是不易于实现的［6］.LU分解适用于非奇异矩阵，并且大规模矩阵的LU分解可以采用块LU分解算法实现，已有进行了基于FPGA的LU分解方法研究的先例［7-9］，并获得了较PC平台更良好的加速性能.但LU分解涉及大量矩阵乘法和除法操作，占用大量FPGA硬件资源，并且导致较大的计算延迟.Cholesky分解仅适用于对称正定矩阵，而对称正定矩阵是一类非常广泛的矩阵，例如网络中产生的矩阵大部分为对称正定阵.虽然Cholesky分解也会产生较大计算延迟的开方操作以及除法运算，但是其计算复杂度只有LU分解的一半.针对此问题，通过引入修正的Cholesky分解算法可以回避开方运算，易于在FPGA上实现.在修正的Cholesky分解中，矩阵C可以分解为L×D×LT.下三角矩阵L和对角矩阵D的计算公式如下:

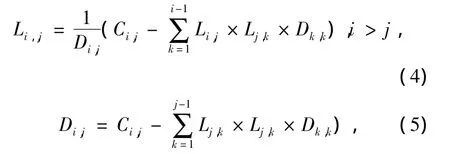
式中:j=1，2，…，n;i=r+1，r+2，…，n.

矩阵L的求逆过程，元素也是相互依存的，因此他们的计算必须按照特定的顺序执行.

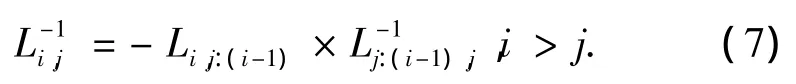
从式(4)可以看出，在计算L的同时得到了D－1，可以存储在RAM中，矩阵C的求逆可以如下得到:

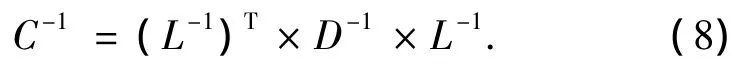
进而通过式(2)得到原始信号的估计.

第三个模块是计算新的残差，为下次迭代做准备:

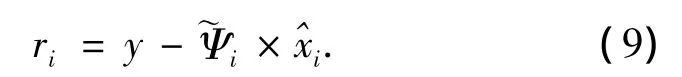
由于OMP算法的迭代性质，不允许3个步骤并行执行，因此只有每个模块依次执行.整体流程图如图1.

2 硬件电路设计

硬件电路由上述3个模块和控制单元组成，具体如图2.主控制单元控制着迭代次数的增加和3个模块的依次进行.下面分别阐述每个模块的具体实施过程.

2.1 寻找最匹配的原子

图1 OMP算法Fig.1 OMP algorithm

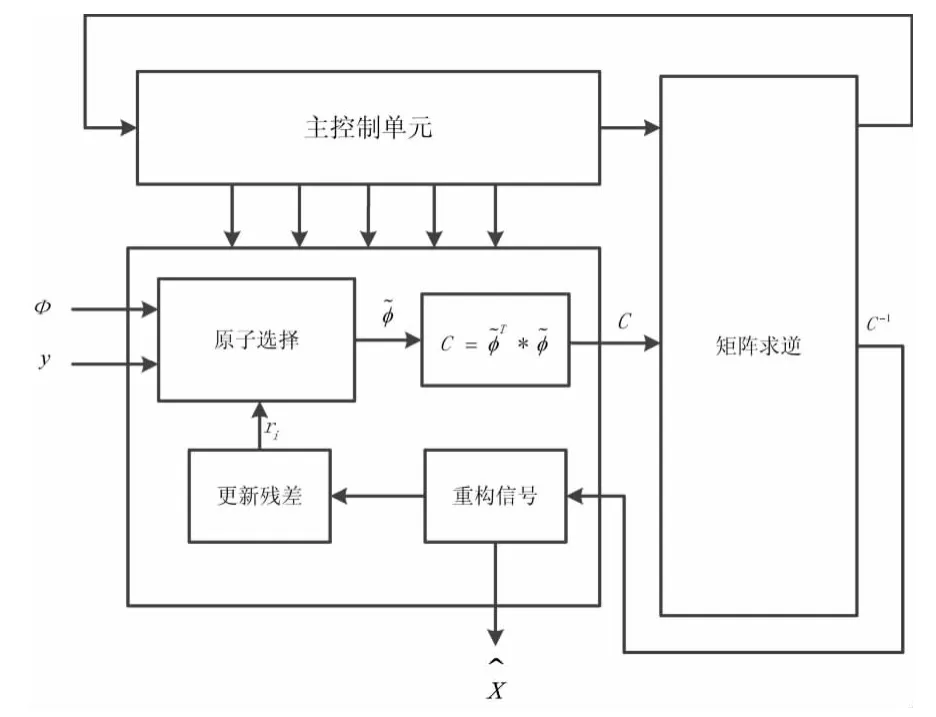
图2 整体硬件电路Fig.2 Overall hardware circuit

在开始执行之前，残差ri由输入的测量向量y∈RN初始化.在执行ΦT×r操作时，由于每个向量和矩阵的列长度为N，设计了N个乘法器和N－1个加法器并行工作，每个乘法器和加法器都是32位.这可以使得向量和向量的乘法在一个时钟周期完成.因此，测量矩阵Φ每一列和残差r的相乘在一个时钟周期完成，使执行复杂度从O(M×N)减少到O(N).原子选择计算点积的结果最大值Wmax和它所在采样矩阵Ф∈RM×N中列的位置被存储在寄存器中供以后使用.具体实现过程如图3所示.

2.2 重构原信号

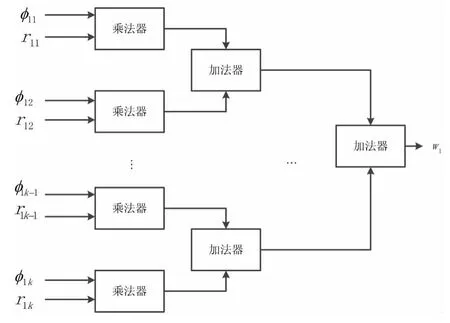
图3 矩阵和向量乘法Fig.3 Matrix and vector multiplication

第二个模块的第一步是通过(3)式计算矩阵C，而~Ψ是由第一个模块原子选择后矩阵扩充所得到的.其结果是一个对称矩阵，可以利用这个来减小计算复杂度.矩阵C的大小从第一次迭代中的1×1增加到k次迭代中的k×k.

第二个模块的第二步是执行矩阵C的逆，改进的Cholesky分解矩阵C和分别计算的分解矩阵的逆，然后再相乘.由提取下三角矩阵L和对角矩阵D，使得C=L×D×LT，以避免平方根的计算.矩阵求逆的硬件电路包括块Cholesky分解电路、L矩阵的求逆电路和块矩阵乘法电路，它们共同完成矩阵的硬件求逆过程.由于L和D这两个矩阵是相互依赖的，因此，计算其元素必须以特定的顺序进行.逆矩阵L的元素也是相互依存的，因此他们的计算必须按照特定的顺序执行.

最后，矩阵C的逆是通过两步得到，如式(5)，先计算 Z=D－1×L－1，然后 C－1=(L－1)T×Z.具体实现过程如图4.

2.3 更新残差

第三个模块计算用于下一次迭代的残差.其中的矩阵向量乘法可以用到第一个模块的结构单元，故而可以达到资源重复利用的目的.

3 仿真及结果分析

测试结果采用的测量矩阵维数为32×128，测量向量维数为32×1，稀疏度k取5，整个过程使用32位定点数表示.图5所示的是Modelsim的功能仿真结果，原信号、用软件和硬件重构的结果比对如图6所示.

图5 Modelism功能仿真Fig.5 Modelsim functional simulation

图6 软硬件结果比对Fig.6 The contrast of hardware and software results

4 结语

本文研究了压缩感知的信号重构算法OMP在FPGA上的一种实现.该设计采用Verilog HDL对OMP算法进行了RTL级描述，采用Altera公司Cyclone III系列FPGA作为硬件平台，并在Quartus II平台上进行了设计和综合，与此同时还进一步在Modlesim平台上进行了功能仿真.从仿真中可以看出精度还不是很好，主要原因是运算过程中全部使用定点数进行计算，而小数位也只保留了8位.由于数据截断造成了很大的误差，如果要改进，必须使用位数更宽的数据，这当然意味着使用更多的逻辑资源.结果表明所占用的资源为9874个LE，最高工作频率可以到达31.28MHz，在利用片上有限资源的情况下所设计设计的硬体结构可以较好地重建原信号.

［1］Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonalmatching pursuit［J］.Information Theory，2007，53(12):4655-4666.

［2］石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，37(5):1070-1081.

［3］Blache P，Rabah H，Amira A.High level prototyping and FPGA implementation of the orthogonal matching pursuit algorithm［C］//ISSPA.Information Science，Signal Processing and their Applications，2012 11th International Conference.Montreal:ISSPA，2012:1336-1340.

［4］Septimus A，Steinberg R.Compressive sampling hardware reconstruction［C］//IEEE.Circuits and Systems，Proceedings of 2010 IEEE International Symposium.New York:IEEE，2010:3316-3319.

［5］周 杰，陈啸洋，赵建勋，等.大矩阵QR分解的FPGA设计与实现［J］.计算机工程与科学，2010，32(10):34-37

［6］Zhang W，Betz V，Rose J.Portable and scalable FPGA-based acceleration of a direct linear system solver［J］.ACM Transactions on Reconfigurable Technology and Systems，2012，5(1):6.

［7］Wu G，Dou Y，Peterson G D.Blocking LU decomposition for FPGAs［C］//IEEE.Proceeding of FCCM'10.Charlotte:IEEE，2010:109-112.

［8］Zhuo L，Prasanna V K.High-performance and parameterized matrix factorization on FPGAs［C］//IEEE.Proceeding of FPL'06.Madrid:IEEE，2006:1-6.