产生有毒物质的浮游植物—浮游动物离散动力学模型分析
顾恩国,张梅娜,陈 博
(中南民族大学 数学与统计学学院,武汉 430074)
一直以来,关于渔业资源的可持续发展的研究有很多,许多学者也建立了大量的模型[1-3],但是近年来,随着对海洋资源可持续利用研究的深入,越来越多的学者注意到位于海洋食物链较低层的浮游生物,对海洋资源的可持续发展有着至关重要的影响,并且由此建立了一系列的数学模型[4-6].在已经建立的模型中,浮游植物、浮游动物相互作用的动态模型大多是在微分方程或者连续动力学基础上提出的,用离散动力学模型进行研究的学者很少,而对于人类的捕捞对浮游生物的影响的研究更是稀少,另一方面,由于部分浮游植物会产生有毒物质,过度累积也会造成浮游动物的死亡.因此,本文将有毒的浮游植物、浮游动物被捕捞的连续模型离散化,建立一个在相同捕捞力度下,浮游植物、浮游动物的变化规律的离散动力学模型,用来研究人类的捕捞力度对整个浮游生物演化的影响,进而讨论对海洋资源可持续利用的影响.
1 模型的建立
Lü Yunfei 和Pei Yongzhen等[5]提出的有毒浮游植物——浮游动物捕捞的连续动力学模型:
(1)
这里,P为在时刻t可产生有毒物质的浮游植物的种群密度,Z为在时刻t浮游动物的种群密度,并且满足在初始时刻P(0)=P0≥0,Z(0)=Z0≥0.r为有毒浮游植物的固有增长率,k为环境对浮游植物的最大承载能力,其中,常数β为浮游动物的最大吸收率,β1为生物量的转化率,d(>0)为浮游动物的自然死亡率,ρ(>0)为单位生物量的浮游植物产生有毒物质的比率,E(≥0)为捕捞力度,c1(≥0)、c2(≥0)为两个种群的可捕系数,α(>0)为Holling type Ⅱ函数的半饱和常数[7].由生物学可知,β>β1>0.
另一方面,假设有毒浮游植物生物量的转化率大于有毒物质的产生比率,即β1>ρ.
在实际生活中,浮游植物、浮游动物的繁殖具有一定的周期性,而人类的捕捞活动也不是时刻不停的,因此离散动力学模型更能反映浮游植物、浮游动物的演化过程.对上述模型进行离散化,可以得到浮游植物、浮游动物捕捞的二维系统如下:
(2)
2 正不动点的存在性
由映射动力系统理论[8]可知,二维动力系统(2)可以写成一个映射动力系统:
(3)
这里′表示时间增加一个单位.任意时刻的映射T表示空间内的一个点(P,Z)映射到下一个点,则系统的轨道:
Γ(P(0),Z(0))={(P(t),Z(t))|(P(t),Z(t))=Tt(P(0),Z(0))}
是映射T从初始点(P(0),Z(0))开始生成的.
下面求系统(3)的不动点,由于系统(3)的不动点必须满足P′=P,Z′=Z,因此求系统(3)的不动点即求解下面非线性方程组的解:
(4)
根据方程组(4)的第一个方程可以得到:P=0或
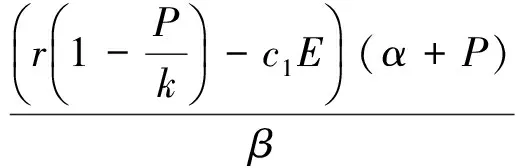
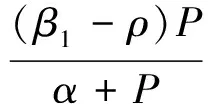
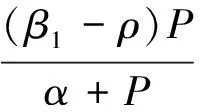

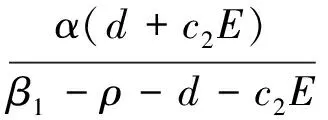
综合上面的分析可知,关于系统非负不动点我们有下面命题1,
命题1 系统除有一个灭绝不动点S0=(0,0)外,还有如下两个非负不动点:



3 不动点的稳定性和分叉
系统(4)在不动点处的局部稳定性取决于其Jacobian矩阵的特征值,在不动点(P,Z)处的Jacobian矩阵有如下形式:
J(P,Z)=

(5)
3.1 灭绝不动点S0=(0,0)的稳定性

证明在S0=(0,0)处系统的Jacobian矩阵为:
其中J(S0)的特征值为λ1=1+r-c1E,λ2=1-d-c2E.
因为max{|λ1|,|λ2|}<1,即|λ1|<1且|λ2|<1时,(0,0)为渐近稳定的.



3.2 边界不动点的稳定性
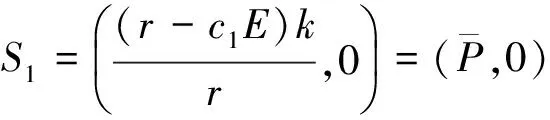

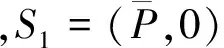
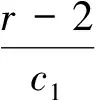



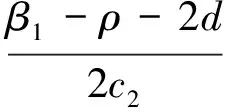



3.3 正不动点S2=(P*,Z*)的稳定性
在S2=(P*,Z*)=
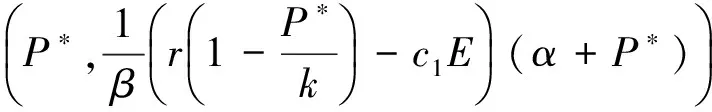



则q2<1成立.
综合上面的分析,可以得到关于正不动点S2=(P*,Z*)的稳定性和局部分叉定理.
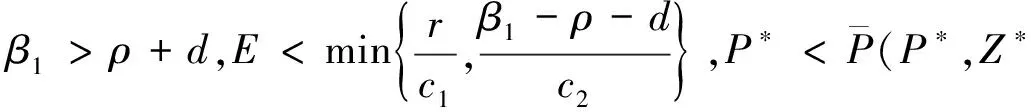
(i)当
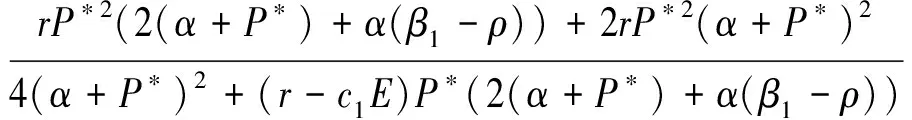
(ii)系统(4)在不动点S2处不可能产生fold分叉;
(iii)当k=




图1 系统(4)关于捕捞力度E的一维分叉图

所以系统在S1=(5.0921,0)处Taylor展式(忽略高阶余项)为:
(6)
上述方程的矩阵形式为:
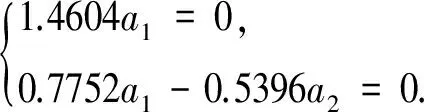
所以映射f1在中心流形上由映射u|→-u+f1(u,h(u)),即u|→-u-0.3928u2+o(u5)给出.
则f1的Schwarzian导数为:
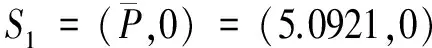
4 结语
本文在假设浮游动物以有毒的浮游植物作为食物,且它们均被人类捕捞的条件下,建立了浮游动物和浮游植物的离散动力学模型,并且对模型进行了非线性分析.我们发现捕捞力度对浮游植物、浮游动物最终的演化有明显的影响,当捕捞力度过小时浮游植物和浮游动物会出现随机或准周期波动,过大会发生灭绝,此时对海洋生态环境而言都不是最佳的.存在捕捞力度的某一阈值范围,此时浮游动植物稳定到一个固定值.当捕捞力度超过某一阈值(例如E>Ec≈10.61)时,相应的以其为食物的较高等浮游动物会灭绝.在单一浮游植物演化中,捕捞力度也有一个较适中的范围,即过高或过低的捕捞力度均不利于浮游植物资源的可持续利用.
[1]Clark C W.Mathematical bioeconomics:the optimal management of renewable resources[M].New York:Wilery,1976.
[2]Gu Enguo.Nonlinear analysis on the dynamical model of common fishery resource[J].Int J of Nonlinear Sciences and Numerical Simulation,2009,10(5):623-634.
[3]Gu Enguo.Complex dynamics analysis for a duopoly model of common fishery resource[J].Nonlinear Dyn,2010,61:579-590.
[4]Saha T,Bandyopadhyay M.Dynamical analysis of toxin producing phytoplankton-zooplankton interactions[J].Nonlinear Analysis:Real World Applications,2009,10:314-332.
[5]Lü Yunfei,Pei Yongzhen,Gao Shujing,et al.Harvesting of a phytoplankton-zooplankton model[J].Nonlinear Analysis: Real World Applications,2010,11:3608-3619.
[6]Gonzalez-Olivares E,Huincahue-Arcos J.A two-patch model for the optimal management of a fishing resource considering a marine protected area[J].Nonlinear Analysis:Real World Applications,2011,12:2489-2499.
[7]Pei Y,Chen L,Zhang Q,et al.Extinction and permanence of one-prey multi-predators of Holling type Ⅱ function response system with implusive biological control[J].J Theoret Biol,2005,235:495-503.
[8]Bischi G I,Naimzada A.Global analysis of a nonlinear model with learning [J].Economic Notes,1997 (26):143-174.
[9]Jury E I.Inners and stability of dynamic[M].New York: Wiley,1974.
[10]Saber N E.Discrete chaos [M].New York: Chapman & Hall/CRC,2000.

