Halo轨道族延拓方法及特性研究

刘磊 刘勇 曹建峰 唐歌实 胡松杰

（1航天飞行动力学技术重点实验室，北京100094）（2北京航天飞行控制中心，北京100094）

1 引言

限制性三体问题的5个平动点及其附近的周期轨道由于独特的空间位置和动力学特性，非常适合于空间观测和中继通信等应用，或者作为深空探测的转移中枢[1]。目前为止，国际上已经成功发射了10个平动点探测器；2011年我国 “嫦娥二号”卫星在探月任务结束后，也进入了日-地月系L2点拟周期轨道开展探测[2]；此外国内外还有多项平动点探测任务处于计划之中。在这些平动点任务的设计阶段，为了满足航天测控能力约束，尤其是探测任务目标的需求，必须首先了解目标平动点周期轨道的周期和运动范围等特性。

平动点周期轨道的理论基础为天体力学中的三体问题，尤其是圆型限制性三体问题，目前国内外对其动力学特性分析和相关解的研究较为充分[3-7]，在Halo轨道族计算尤其是族参数选择、族周期和幅值的变化特性等方面的研究则相对有限。为了全面了解平动点大范围Halo轨道的周期和运动范围等特性，可以研究平动点附近的Halo轨道族。不过，由于Halo轨道族计算受族参数影响较大，在某些特定族参数下大幅值Halo轨道迭代不收敛，或者迭代结果与初值相差较大，不能得到完整连续的Halo轨道族。

因此，本文基于微分修正和延拓法研究了Halo轨道族计算及其运动特性，克服了传统Halo轨道设计方法在大幅值Halo轨道和完整Halo轨道族数值计算上的缺陷，得到了日-地月系，尤其是地月系共线平动点连续完整的大范围南北Halo轨道族，可用于我国未来深空探测的平动点任务设计。

2 数学模型

2.1 Halo轨道设计

限制性三体问题中，第三体的质量远小于两个大天体的质量。首先将质量、长度和时间单位归一化[6]，记μ为质量稍小的大天体相对于两个大天体质量之和的比值；其次以两大天体的质心为原点O，两大天体的连线为x轴，相对运动平面为xy平面，建立旋转坐标系或称会合坐标系。在圆型限制性三体问题下，建立小天体在坐标系Oxyz中的动力学方程：

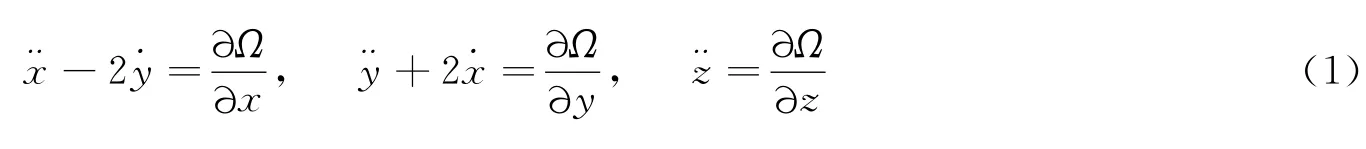
式中Ω为等效势[6]。

在平动点附近的运动相对于平动点的偏差Δx、Δy和Δz为小量的情况下，将式（1）在平动点附近作一阶展开，得到平动点附近周期运动的解析形式为

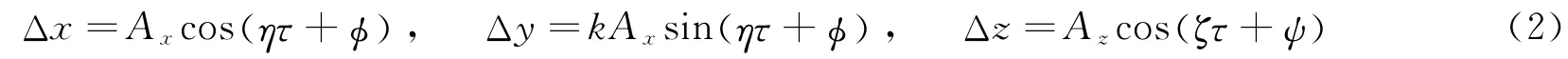
式中Ax和Az分别为x和z方向的运动幅值；η和ζ分别为x和z方向的运动频率，当运动幅值充分大时，非线性项的影响可能使得二者相等，从而形成Halo轨道；φ和ψ分别为x和z方向的初始相位。

由式（2）可见，Halo轨道关于xz平面对称，且在xz平面附近运动方向垂直于xz平面，这一性质对于Halo轨道的数值设计至关重要。Halo轨道数值设计的迭代初值可采用式（2）。如果对于初值要求较高，则可以基于式（2），由Lindstedt-Poincaré法得到共线平动点Halo轨道的三阶近似解[6]。

微分修正中，利用Halo轨道的对称性，可选择初始状态x0位于xz平面，在动力学模型式（1）下由x0积分t时刻至末状态xd，通过修正x0和t使得xd位于xz平面且满足Halo轨道特性，即x和z方向速度为0，设xd的偏差量为δxd，修正量分别为δx0和δt，则迭代过程为

式中Φij（i＝2，4，6；j＝1，3，5）表示状态转移阵Φ（t1；t0）的第i行第j列个分量[3]。Φ（t1；t0）建立了由初始状态到末状态的单步线性估计，也体现了末状态对初始状态的敏感性，如果考虑其余天体引力和光压等摄动，则修改式（1）右端即可求解出对应的状态转移矩阵，即得完整力模型下的Halo轨道（族）。

2.2 Halo轨道族参数与延拓计算

式（3）为欠定方程组，一般固定一个待求参数后有确定解，这个固定参数即定义为Halo轨道族的族参数，由此可选择x0、z0、0或周期T作为族参数，不过有些情况下会出现迭代不收敛情况。同时需指出，除族参数外的其余参数应同步求解，文献[3]中虽然也是固定z0，但是迭代时先积分至xz平面，然后改正x0和z0使得末状态和为0，该方法对于大幅值Halo轨道会出现迭代发散现象，其原因在于预先施加约束而构造的迭代序列偏离了真实的轨道解。

式（3）还可以采用最小二乘法求解，其优点在于收敛性较好，大幅值Halo轨道也可以收敛。不过，由于所有参数均参与迭代改正，没有反映族特征的明显族参数，此时虽然可以考虑选择相关的Halo轨道幅值Ax或Az作为族参数，然而数值计算表明，轨道幅值较大时的最终结果与迭代初值相差较大，往往收敛于平面Lyapunov轨道，且得到的Halo轨道族连续性较差。

选定族参数后，基于式（3）计算Halo轨道族。鉴于微分修正法极大地依赖于x0与真实解的逼近程度，大幅值Halo轨道计算时可能出现迭代发散，考虑采用延拓法计算Halo轨道族初值。延拓法是一种求解非线性方程组的大范围收敛算法[8]，对x0与真实解的逼近程度要求较低。对于如下非线性方程组

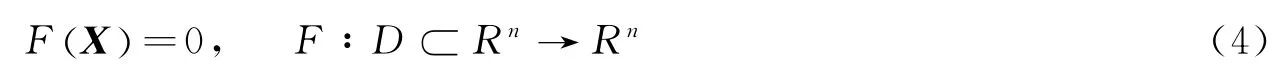
延拓法的思想就是构造一族映象H∶D×[0，1]⊂Rn＋1→Rn，且有

其中F0X（）＝0的解X0已知，H（X，1）＝0的解即式（4）的解，于是式（4）的求解转化为求如下同伦方程组的解Xν（）

式（3）对应于延拓法中的待求问题F（X），除族参数以外的变量即待求参数X，族参数即同伦方程组变量ν。利用延拓法计算Halo轨道族，首先在平动点附近利用Halo轨道高阶解和微分修正法，计算初始标称轨道，即式（5）中F0X（）＝0的解X0；其次，选择同伦方程组变量ν，选取步长Δν，利用式（3）计算族参数增加步长Δν后X0的其余状态参数的改变量，从而得到新的X0；最后，利用微分修正法迭代求解族参数增加步长Δν后的Halo轨道。

为了分析Halo轨道族的运动区域，定义微分修正后的Halo轨道在x和z方向的幅值为

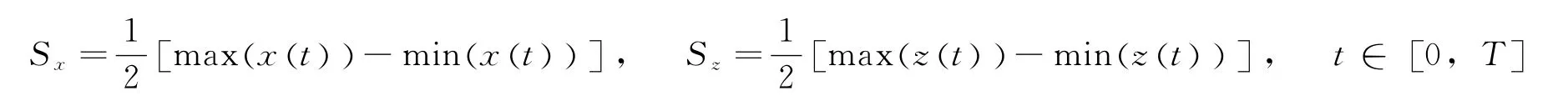
3 数值仿真

由于地月系的μ值远大于日-地月系，因而二者Halo轨道族特性差别较大，同时L1和L2点附近的动力学特性差别使得各自附近的运动也不相同。因此，本节数值计算地月系和日-地月系L1和L2点的南北Halo轨道族，给出轨道族的周期和运动幅值变化，通过计算给出最大的固定延拓步长，同时研究族参数选择对Halo轨道族计算的影响。

3.1 日-地月系Halo轨道族

选择x0作为族参数计算L1点北族Halo轨道，如图1所示。图1中○表示各Halo轨道的初始位置状态，●和■分别表示L1点和地月系质心，曲线为轨道族中的Halo轨道。

由图1可见，Halo轨道族在x方向由L1点拓展至地月系质心，但是y和z方向上运动范围有限。L1点附近的Halo轨道相对于yz面倾角最小，在地月系质心附近倾角最大。另外，仿真中发现延拓步长最大可达10-5，如果进一步增大步长，则对初始轨道要求苛刻，迭代一般收敛于平面Lyapunov轨道。

L1点北族Halo轨道族的轨道周期和运动幅值随族参数x0的变化如图2中的T1和Sx1及Sz1所示。为直观起见，图2中将x0转换为相对于地月系质心的距离dx。以x0作为族参数计算L1点南族Halo轨道族，其周期T和运动幅值的变化与图2中的T1和Sx1及Sz1完全相同，充分反映了南北Halo轨道族的对称性。此外，以x0作为族参数计算L2点南北族Halo轨道族，其周期T约为110～180天，运动幅值Sx和Sz与L1点Halo轨道族基本相同。

选择0作为族参数无法计算得到L1点南北族整个Halo轨道族。不过，可以获得L2点南北族整个Halo轨道族，尤其是可以将轨道族延拓到地月系质心附近很小范围内，轨道周期和幅值的变化如图2中的T2和运动幅值Sx2及Sz2所示。

图1 日-地月系L1点北族Halo轨道族Fig.1 North halo family of the libration point L1in the Sun-Earth／Moon system

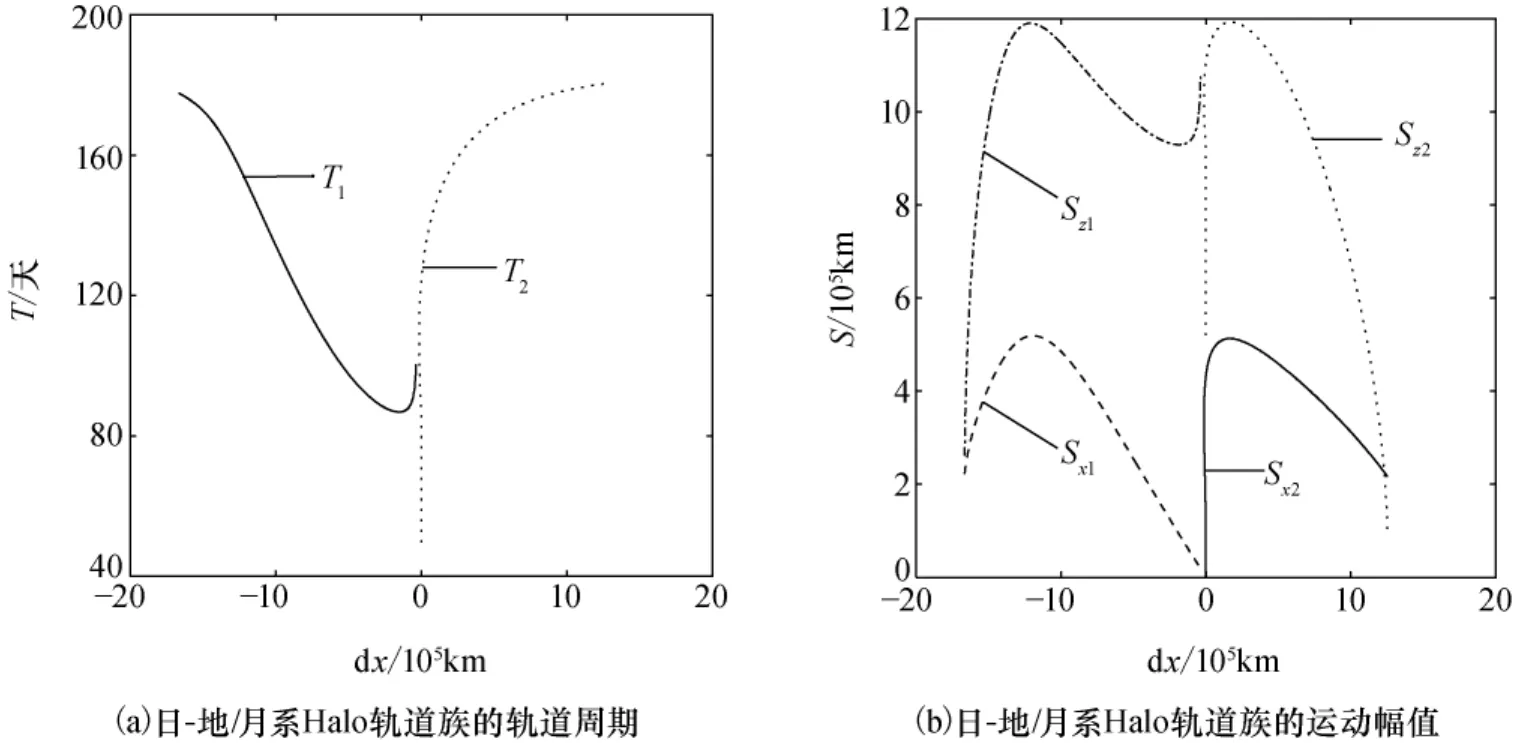
图2 日-地月系L1点和L2点Halo轨道族的周期与幅值Fig.2 Periods and scopes of the halo family of the libration point L1and L2in the Sun-Earth／Moon system

由图2可见，周期T2的变化范围大于T1，二者最大值较为接近，但是T2最小可达约48天。Halo轨道族的运动幅值Sz大于Sx，Sz最大可达1.2×106km，Sx最大仅为5×105km。另外，虽然L1和L2点Halo轨道族在x和z方向的运动幅值的变化趋势有所差异，但是它们的变化范围大致相同，且均在平动点与地月系质心之间的某个位置出现最大值。

如果选择z0作为族参数，则无法得到L1点和L2点的整个南北Halo轨道族。经过分析可知，Halo轨道族在xz平面上沿z轴并非单调变化，固定步长延拓失效，需要采用较为复杂的延拓步长调整策略。如果选择T作为族参数，可以得到L1点附近绝大部分南北Halo轨道族。至于L2点附近，选择T作为族参数的结果优于选择x0，其原因在于固定延拓步长下x0失效时仍然可以用T延拓。

本文计算了日-地月系L1和L2点的南北Halo轨道族，每个轨道族均用4个族参数进行计算，共计16种情况，限于篇幅，且南北轨道族关于xy平面对称，仅给出L1和L2点北族Halo轨道族仿真结果，如表1所示，其中Spx和Spz分别为Halo轨道族在x和z方向上距地月系质心的变化范围，P为轨道周期范围，τ为最大延拓步长。除τ外，其余各参数均给出变化范围。

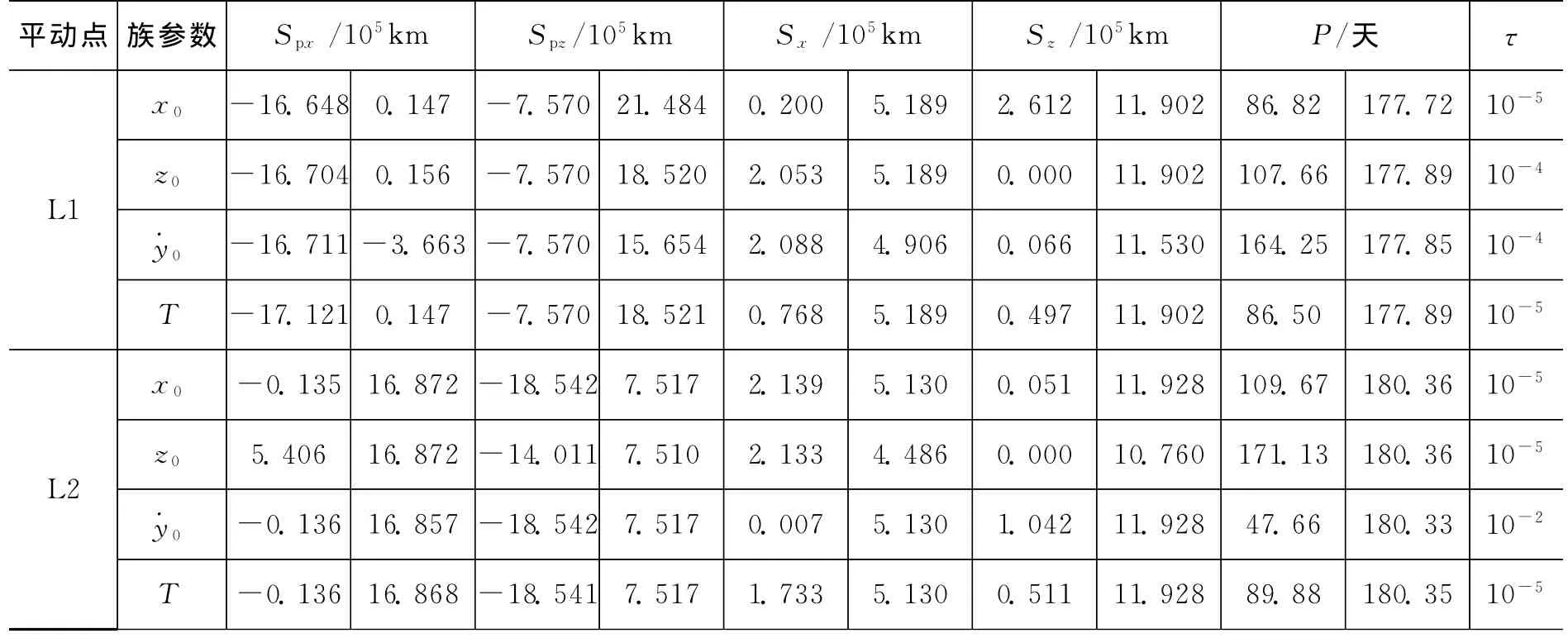
表1 日-地月系Halo轨道族特性Tab.1 Characteristics of the halo family in the Sun-Earth／Moon system

由表1可见，Sx的最小范围在以0为族参数时最小可达到约700km，选择其余族参数时最大不超过2.2×105km，文献[6]中由三阶解析解给出的最小值约为2×105km，由此可见数值计算得到的Halo轨道族可达范围远大于三阶解析解结果，同时，日-地月系L1点Halo轨道族应选择T或x作为族参数，L2点轨道族应选择或T作为族参数。表1中的各项参数可为平动点任务设计提供非常有益的参考。

3.2 地月系Halo轨道族

地月L1点南北轨道族，以z0作为族参数的范围最大，如图3所示，注意此处AU为地月距，■表示月球。

由图3可见，轨道族从L1点向月球拓展，到达月球后仍可进一步拓展，z0最大可以达到1个地月距左右，将之与图2对比，充分说明了不同三体系统的周期轨道运动范围并不完全相同。轨道周期T由13.5天降低到最低约8天后，又快速增加到约12天，Sx和Sz的变化也较为复杂，且南族Halo轨道族的变化与北族类似，限于篇幅，此处略去变化图。

以其余族参数得到的L1轨道族中，仅以x0为族参数的结果与以z0为族参数的结果接近，以0和T为族参数的结果较差。对于L2点南北轨道族，以0作为族参数的结果范围最大，其周期和幅值变化趋势与以0为族参数的日-地月系L2点结果相同。以x0和T为族参数的结果略差于以0为族参数的结果，以z0为族参数的结果最差。因此，地月系L1点Halo轨道族应选择z或x作为族参数，L2点轨道族应选择y方向速度或T作为族参数。

地月系L1和L2点的北Halo轨道族特性如表2所示，其中仅给出较好的族参数结果。

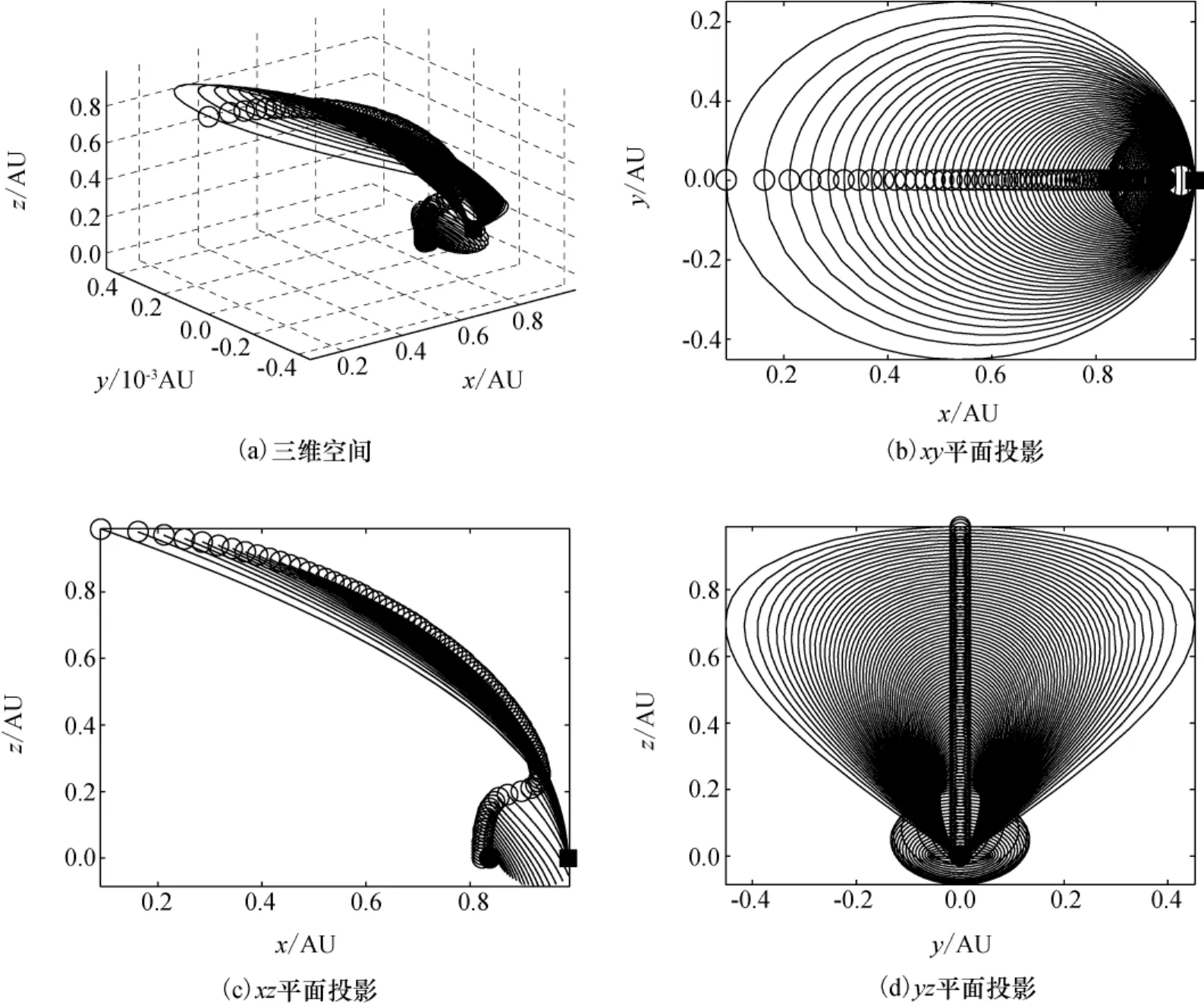
图3 地月系L1点北族Halo轨道族Fig.3 North halo family of the libration point L1in the Earth-Moon system

表2 地月系Halo轨道族特性Tab.2 Characteristics of the halo family in the Earth-Moon system

由表2可见，地月系L1点Halo轨道族在x和z方向的可达范围和运动幅值远大于L2点Halo轨道族，不过轨道周期的变化范围小于L2点Halo轨道族。另外，L2点Halo轨道族的延拓步长最大可以达到0.1，L1点也可以达到10-3，远远大于表1中日-地月系情况。

4 结束语

在圆型限制性三体问题下，基于延拓法研究了固定步长下族参数选择对Halo轨道族计算的影响，给出了各Halo轨道族的轨道周期和空间位置变化特性。研究表明，日-地月系L1点Halo轨道族应选择轨道周期T或会合坐标系x坐标作为族参数，L2点轨道族应选择y方向速度或T作为族参数；地月系L1点Halo轨道族应选择z或x作为族参数，L2点轨道族应选择y方向速度或T作为族参数，且数值计算得到的Halo轨道族运动范围大于解析解。

文中仅用固定延拓步长即可得到大幅值周期轨道和连续完整的周期轨道族，可用于任意三体系统平动点周期轨道族计算，不过研究中发现固定延拓步长情况下族参数的选择影响很大，如果不是单调变化，则无法得到整个Halo轨道族。因此，后续研究计划将考虑族参数的变化特性，制定变步长计算策略。

[1]LO M W.The interplanetary superhighway and the origins program，IEEE Space 2002Conference[C].IEEE，Big Sky，MT，US，March 9-16，2002.

[2]WU WEIREN，LIU YONG，LIU LEI，et al.Pre-LOI trajectory maneuvers of CHANG′E-2libration point mission [J].SCIENCE CHINA，2012，55（6）：1249-1258.

[3]CHOW NAOMI，GRALLA ERICA.Low earth orbit constellation design using the Earth-Moon L1point[D].New Jersey：Princeton University，2004.

[4]HOWELL K C.Families of orbits in the vicinity of the collinear libration points[J].Journal of the Astronautic Sciences，2001，49（1）：107-125.

[5]CORS J M，PINYOL C，SOLER J.Periodic solutions in the spatial elliptic restricted three-body problem [J].Physica D，2001，154：195-206.

[6]RICHARDSON D L.Analytic construction of periodic orbits about the collinear points [J].Celestial Mechanics and Dynamical Astronomy，1980，22（3）：241-253.

[7]侯锡云.平动点的动力学特征及其应用 [D].南京：南京大学，2008.HOU XIYUN.Dynamics and their applications of libration points[D].Nanjing：Nanjing University，2008.

[8]李庆扬，莫孜中，祁力群.非线性方程组的数值解法 [M].北京：科学出版社，1997.LI QINGYANG，MO ZIZHONG，QI LIQUN.Numerical methods for non-linear equation group [M].Beijing：Science Press，1997.