基于SSA和BSS的单通道盲信号分离算法

于宁宇 马红光 姜勤波 石磊

（1第二炮兵工程大学，西安710025）（2解放军96656部队，北京100028）

1 引言

现代空间环境中，电子侦察接收机截获到的信号具有时域高度密集、频域极度交叠的特性，而现有的信号处理技术几乎都是针对单信号而言的，因此如何实现复杂电磁环境中源信号的分离成为空间侦察中遇到的一个急需解决的实际问题。利用源信号的空间差异进而采用盲源分离算法 （Blind Source Separation，BSS）是解决该问题的一个有效方法，然而单通道宽带接收机仍为实际应用中的主流装备，因此对单通道盲源分离（Single-Channel Blind Source Separation，SCBSS）的研究仍旧是目前的热点问题，大量的文献针对不同的应用提出了不同的方法。文献[1]利用过采样和抽头延迟将单通道接收机收到的双路MPSK信号转化为伪阵列信号，进而利用独立分量分析算法（ICA）实现信号分离，其要求两路信号成型脉冲具有差异；文献[2]首先利用ICA训练信号子空间，进而估计系数实现SCBSS，需要先验信息；文献[3]针对单通道音频信号进行研究，同样需要对源信号进行训练或者已知源信号的特性；文献[4]融合了经验模式分解（EMD）和独立分量分析（ICA）方法实现了单通道医学信号的分离，但是EMD方法理论上不够完善；文献[5-9]为国内学者在特殊应用背景下的SCBSS研究成果，对解决空间侦查中的信号分离失效。为解决该问题，文献[10]提出了融合奇异谱分析（Singular Spectrum Analysis，SSA）和盲源分离算法（BSS）的单通道盲源分离思路，从理论上分析了该算法实施过程中需要注意的关键参数设置，并利用实测的数据验证了算法的效果，但是对算法性能分析较少，本文作为其补充和改进，期待对解决空间侦察中经常遇到的SCBSS问题提供较为完善的解决方法。

2 信号模型

假设空间截获接收机同时接收到M个独立辐射源信号，信号范围为常用的单频信号、线性调频信号和相移键控信号；时域完全重叠，频域可以重叠也可以不重叠；并伴随着高斯白噪声，此时宽带接收机截获到的信号为

式中M为信源数；si（t），ai，i＝1，2，…，M分别为独立源信号和加权系数；w（t）是均值为0、方差为σ2w的高斯白噪声；r（t）为1×N的混合信号；si（t）为第i个源信号。利用BSS算法的假设，设源信号之间相互统计独立，源信号中至多只有一个服从高斯分布。上述假设在实际环境下很容易满足，这是因为：各个信号由不同辐射源发出，因此具备独立性，况且实际环境中满足严格高斯分布的信号几乎不存在。本文的目的为仅利用单路接收数据实现各独立辐射源信号波形的恢复或者信息码元的提取，并考察其分离性能。

3 算法描述

3.1 基于SSA的伪阵列构建

SSA是一种适合从短时平稳时间序列中提取信息的方法，因此要求待处理数据平稳，文献[10]对如何从非平稳数据中截取平稳数据进行了研究，本文利用文献[10]所提方法对待处理数据进行平稳性判定，获取到平稳时间序列。SSA通过对所谓的延迟协方差矩阵进行特征值分解来寻找时间序列的内部结构，不需要选择结构函数作为先验信息，这也是本算法称之为盲分离算法的本质，标准的SSA步骤可以参考文献[10-11]，本文对其简化，去除了主分量分析过程，描述如下。

步骤1：对于接收到的一维数据＝r（t）｛ ｝，t＝1，…，L，…，N，选择窗口长度L[10]（L大于信源数即可），构建L×（N-L＋1）维数据矩阵R

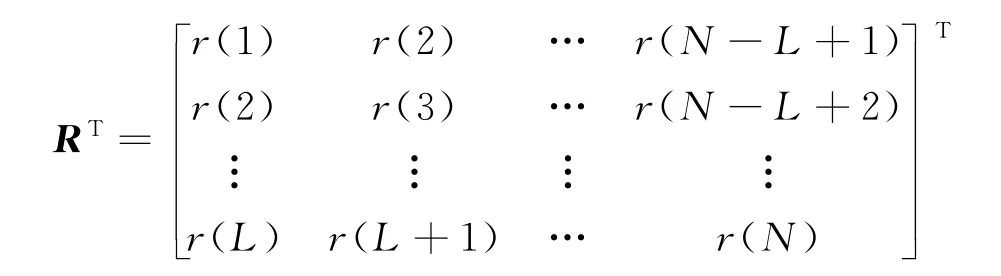
步骤2：R的自协方差矩阵为｝，其为Toeplitz矩阵，对其进行特征值分解[V，D]＝eig（CR），其中，eig（·）表示特征值分解；D为L个特征值λj，1≤j≤L按照降序排列的特征值矩阵，V为特征值对应的特征向量；最大特征值对应的特征向量称为第一阶模式，次大特征值对应的特征向量称为第二阶模式；第一阶模式代表了信号的最大变化趋势，第二阶模式代表了与第一阶模式无关的剩余信号量的最大变化趋势，依次类推。在实际分析过程中，通常只选取前面的低阶模式进行分析，即通过对其进行主分量分析达到简化计算、降低噪声的目的，本节主要目的是利用SSA将单通道数据转化为正定的阵列数据，故不需要考虑主分量分析。

步骤3：对第j，1≤j≤L个特征向量vj而言，其张成的特征空间为vjvTj，则矩阵R在该特征空间上的投影为

步骤4：SSA最关键的一步为成分重构，其实现是通过反Hankel变换得到的。由步骤3可知第j（1≤j≤L）个投影矩阵Wj为L×（N-L＋1）维矩阵，其反Hankel变换的实现过程为

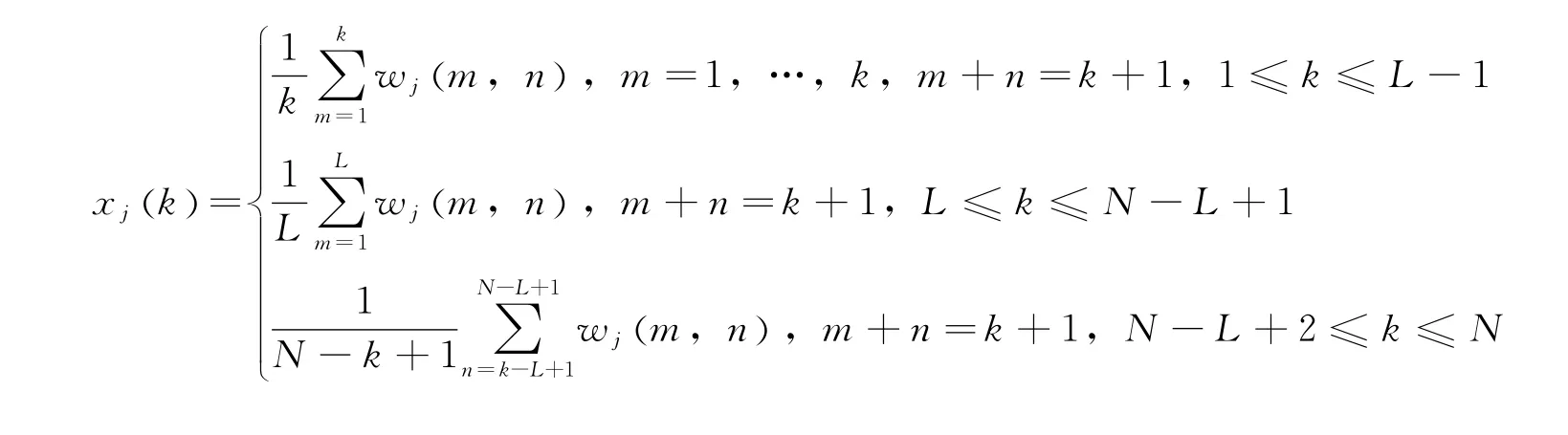
则Xj＝｛xj｝为1×N维向量，同理可以获取X＝ [X1；X2；…；XL]为L×N的阵列，满足BSS算法要求阵列数目大于源信号数目的基本假设。

3.2 BSS算法描述

由3.1节可知，SSA将单通道数据转换成了满足BSS算法要求的阵列数据，下面采用成熟的BSS算法-AMUSE[12]算法实现信号分量的分离，其步骤如下。

步骤5：求伪阵列信号X的协方差矩阵对其特征值分解[UX，DX]＝eig （CX），获取白化矩阵

步骤7：对进行特征值分解，P即为分离矩阵。

步骤8：输出分离信号为：Y＝P×Z。

4 算法性能分析

4.1 复杂度分析

综述3.1节和3.2节描述的算法过程，以窗口每滑动一次为1个时间单位；加、减法计算量相当，为1个时间单位；开方、除法需要两个乘法的计算量；L×L的矩阵特征值分解的计算量为L3。设数据点数为N，数据窗宽度为L，则算法每一步的计算复杂度如表1所示。若加法运算和乘法运算计算量相当，则总的计算复杂度为2NL3-2L4＋5L3＋4NL2-5L2＋6NL＋5N＋12L＋3，若N＝5 000，L＝10，计算复杂度为1.2×108个时间单位，现有的工程计算机完全可以快速实现。

表1 算法的计算复杂度Tab.1 Computational complexity of the algorithm

4.2 分离性能评价准则

针对不同的源信号，利用不同的评价准则进行分离性能的评估。对于雷达信号中常用的单频信号或者线性调频信号，相似系数或输出波形均可作为算法性能评估准则。相似系数是衡量盲信号分离算法性能的一个指标，定义为

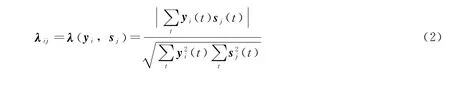
式中

yi

、

sj

分别表示两路信号矢量；

λij

表征两个信号矢量之间的相似程度，消除了幅值的不确定性。当由相似系数构成的相似系数矩阵每行每列都有且仅有一个元素近似于1，而其他元素近似于0，可认为算法分离效果理想。

对于携带信息码元的相移键控信号而言，考察相似系数或者频域波形意义不大，其本质是携带信息码元的恢复，因此考虑对分离后的信号解码，进而考察其误码率。误码率定义为错误码元的个数与整个发送码元个数之比，其更能确切表达分离效果，一般认为误码率小于0.01时分离效果较好。

5 仿真试验

为了验证本文所提算法的性能，以电子侦察中常用的单频信号、线性调频信号和相移键控信号为例，考察算法的分离性能。下文中信噪比定义为混合信号总能量和噪声能量之比的10倍对数值，信干比定义为信号1能量和信号2能量之比的10倍对数值。

（1）仿真试验1

首先考察算法对雷达中常用的单频信号和线性调频信号的分离情况，其中单频信号频率分别为150MHz和350MHz；线性调频信号为250MHz～280MHz，采样频率为1GHz，采样时间为2μs，即采样点数为2 000点。构建伪阵列信号时，L由文献[10]可以计算为10。混合数据的时域和频域波形如图1所示，由图1（b）可以看出，频域上出现3个明显的尖峰，故信号个数为3；经SSA张成的滤波器的频域波形如图2所示（为了清晰，仅仅画出3组滤波器频域波形），其中最上面的曲线为原信号的频谱。SSA方法不依赖任何先验信息，仅由数据内部时序结构决定，故其类似于自适应频域滤波[10-11]，可以将单通道数据转化成阵列数据。

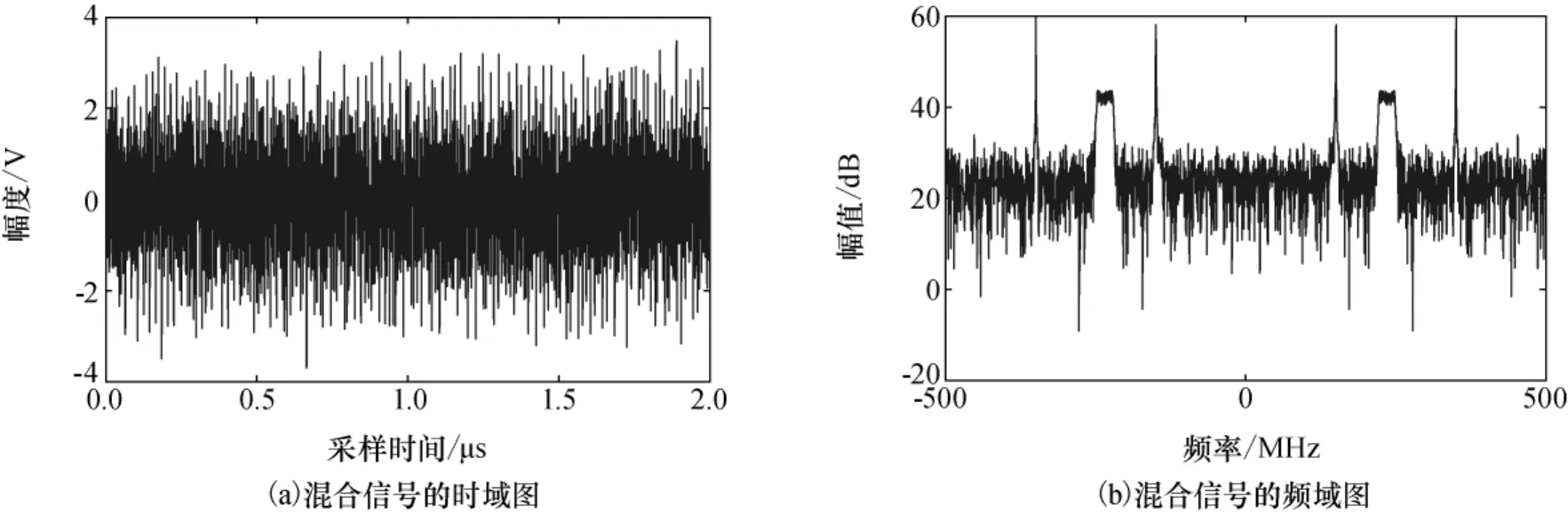
图1 混合信号的时域及频域Fig.1 Diagrams of the mixed signal in time and frequency domains

图3 为算法输出的信号的频域波形，可以看出，本文所提的单通道盲信号分离算法可以有效地分离出单通道频域没有重叠的信号，具有自适应性，故称之为盲分离算法，对其他信号分量的压制超过了20dB。进一步，为了考察其性能，利用式（2）定义的相似系数考察分离性能，得到的结果如图4所示，可以看出，当信噪比大于6dB时，相似系数均大于0.9，可以认为完全实现了单通道盲信号分离。

（2）仿真试验2

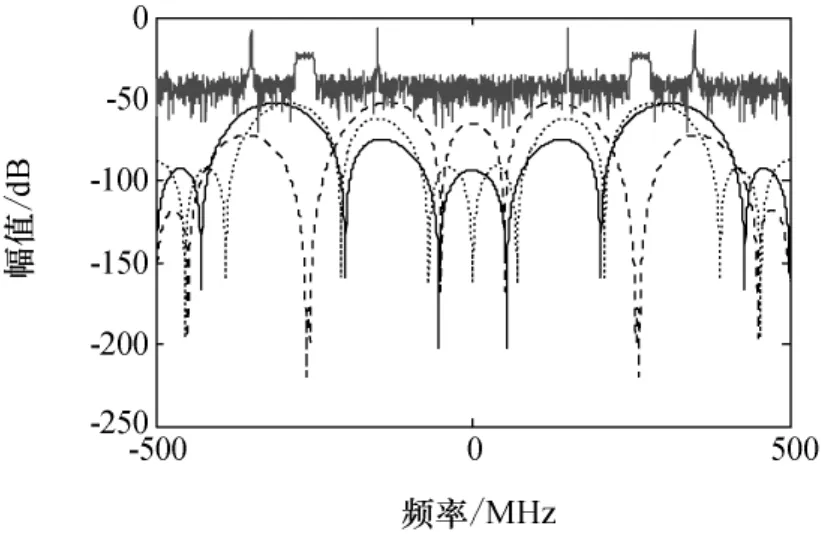
图2 SSA张成滤波器的频域Fig.2 Diagram of the filters spread by SSA in frequency domain

图3 输出信号的频域Fig.3 Diagrams of the separated signals in frequency domain

为了验证该方法对常用的BPSK信号的分离能力，首先考察频谱没有重叠的双BPSK信号，参数设置为：信号1的载频为0.2，码元宽度为120；信号2的载频为0.3，码元宽度为120；采样频率设置为归一化采样频率1，两路信号的信息码随机产生。理论上，可以利用频域滤波器实现信号分离，但是SSA方法可以利用信号内部结构自适应的实现信号分离；分离后的两路信号信息码恢复情况如图5所示。其中，图5（a）、（b）中上面图形中实线为分离信号经下变频和低通滤波后的波形；虚线为整形后的波形；下面图形中 “＊”为源信息码；“Δ”为恢复信息码；可以看出，恢复的信息码可能具有极性差异，但是不影响信息的获取。算法中窗口长度设为10，信号个数为2，信噪比为20dB。

图4 相似系数随信噪比的变化图Fig.4 Diagram of the correlation coefficient versus with SNR

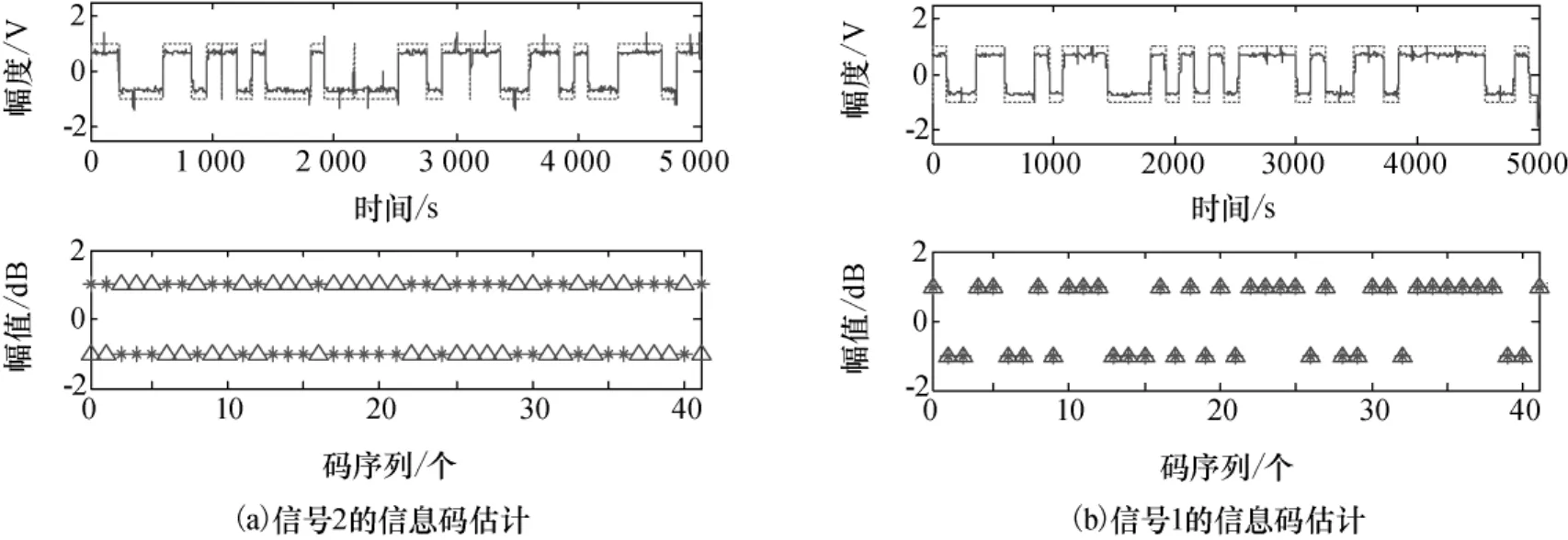
图5 分离信号的信息码估计和源信息码比较Fig.5 Diagrams of the estimation symbol and the source symbol

上面试验是在固定信噪比的情况下信号分离情况，下面将考察算法对噪声的适应性。当信干比为0dB时（即等功率），两路信号各自的误码率随信噪比变化的曲线如图6所示。可以看出，本文算法在信噪比为4dB时误码率小于0.01，可以认为信号完全分离。

上述试验是在双信号等功率时的误码率随信噪比变化的情况，下面试验将考察当双信号功率比相差较大时，算法对两信号的分离能力。当信干比为30dB时，即信号1的能量为信号2的能量的1000倍时，经过单通道盲分离算法后，信息码提取情况如图7所示，此时信号2为弱信号，信噪比为20dB。

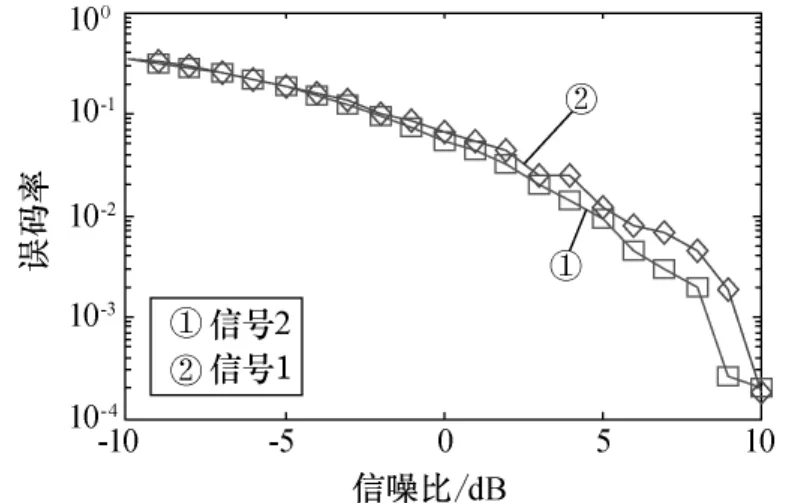
图6 等功率下误码率随信噪比变化Fig.6 Diagram of the bit error rate versus with SNR under the same power

由图7可知，该算法对单通道频谱不重叠的信号分离效果稳健；当信干比为30dB时，对弱信号的带宽估计困难，此时带通滤波器设计同样困难，但是本文方法仍能根据信号本身固有的特性自适应的实现单通道盲信号分离。

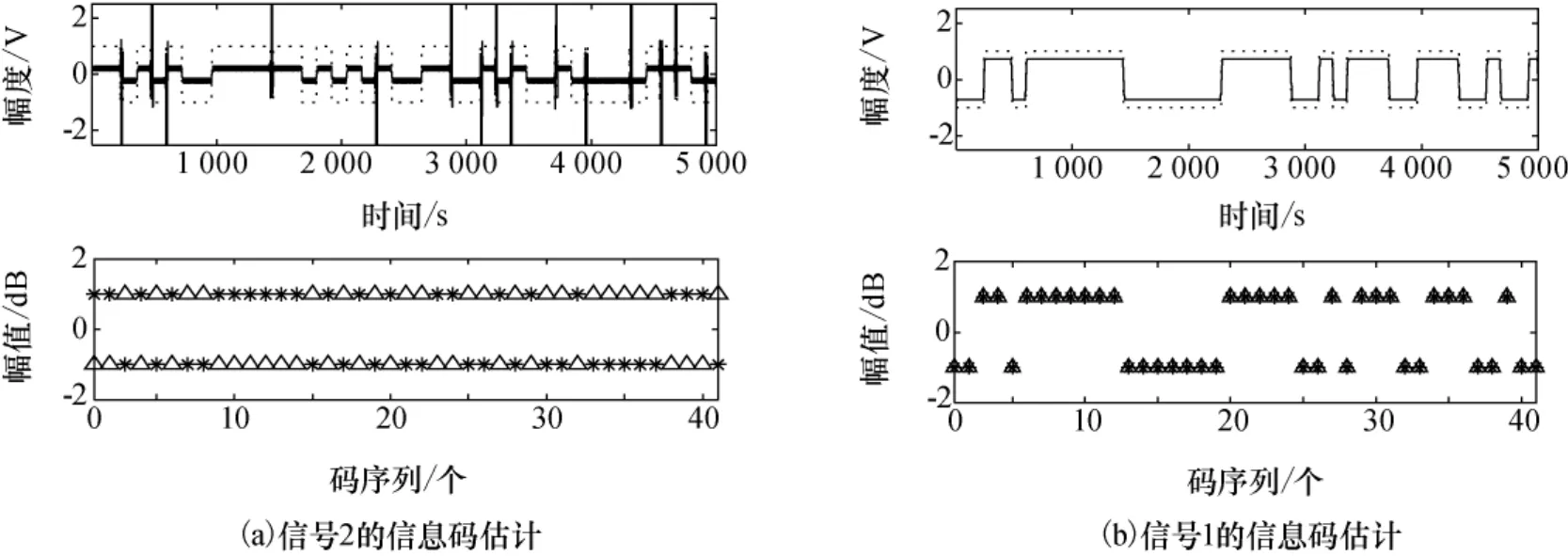
图7 信干比为30dB时信息码估计和源信息码比较Fig.7 Diagrams of the estimation symbol and the source symbol when SIR is 30dB

（3）仿真试验3

上述试验是针对频谱不重叠的信号进行的分离，考察其频谱分辨率，设信号1的载频为0.2，信号2的载频在0.2～0.3之间并以0.01的步进，此时双信号的频谱由完全重叠到逐步分离。当信噪比为20dB、信干比为0dB时，其误码率随载频变化曲线如图8所示。

由图8可以看出，SSA算法的频率分辨率并不好，其要求待处理的单通道混合数据中各个独立源信号频率不重叠且分离度较大，但是对于实际中单通道宽带接收机截获到多个频率分离较大的窄带信号且能量相差较大的实际情形而言，是可行的，文献[10]中已经描述。课题组后续的工作将针对本算法不能解决的单通道频谱逐步靠近以至于完全重叠的情形展开研究。

图8 误码率随信号2载频变化Fig.8 Diagram of the bit error rate versus with carrier frequency of signal 2

6 结束语

针对复杂电磁环境下宽带接收机截获到多信号情况，提出了一种融合SSA和BSS的单通道盲信号分离算法。该算法首先利用SSA构建伪阵列信号，进而采用BSS算法实现信号分离，并对算法的计算复杂度进行了分析。最后利用几种常见的信号——单频信号、线性调频信号和相移键控信号进行了仿真验证，试验结果表明：该算法能有效地解决单通道宽带接收机截获到多个频谱分离度较大、能量相差较大的窄带信号，但是在面临频谱相近或者重叠的多信号时，算法失效，后续的研究将针对此类信号展开。

[1]WARNER E S，PROUDLER I K.Single-channel blind signal separation of filtered MPSK signals [J].IEEE Proceeding Radar Sonar Navigation，2003，150（6）：396-402.

[2]JANG GILJIN，LEE TE WON.Single-channel Signal Separation Using Time-domain Basis Functions [J].IEEE Signal Processing Letters，2003，10（6）：168-171.

[3]MATHIEU P，LAURENT G，JEAN M B.A Watermarking-Based Method for Informed Source Separation of Audio Signals with a Single Sensor [J].IEEE Transactions on Audio，Speech and Language Processing，2010，18（6）：1464-1475.

[4]BOGDAN M，MAARTEN D V，IVAN G，et al.Source Separation From Single-Channel Recordings by Combining Empirical-Mode Decomposition and Independent Component Analysis [J].IEEE Transactions on Biomedical Engineering，2010，57（9）：2188-2196.

[5]涂世龙，陈越新，郑辉.利用纠错编码的同频调制混合信号单通道盲分离 [J].电子与信息学报，2009，31（9）：2113-2117.TU SHILONG，CHEN YUEXIN，ZHENG HUI.Exploiting Error-control Codes in Single-channel Blind Separation of Co-frequency Modulated Signals [J].Journal of Electronics ＆Information Technology，2009，31（9）：2113-2117.

[6]涂世龙，郑辉.同频不同速率数字调制混合信号的单通道盲分离 [J].电路与系统学报，2010，15（3）：43-47.TU SHILONG，ZHENG HUI.Single-channel Blind Separation of Dignal Modulated Signals with Close Carriers and Different Data Rates[J].Journal of Circuits and Systems，2010，15（3）：43-47.

[7]崔荣涛，李辉，万坚，等.一种基于过采样的单通道MPSK信号盲分离算法 [J].电子与信息学报，2009，31（3）：566-569.CUI RONGTAO，LI HUI，WAN JIAN，et al.An Over-sampling Based Blind Separation Algorithm of Single Channel MPSK Signals[J].Journal of Electronics＆Information Technology，2009，31（3）：566-569.

[8]彭耿，王丰华，黄知涛，等.单通道混合信号中周期信号的盲分离 [J].湖南大学学报，2010，37（4）：42-45.PENG GENG，WANG FENGHUA，HUANG ZHITAO，et al.Blind Periodic Signal Separation of Single Channel Composite Signal[J].Journal of Hunan University，2010，37（4）：42-45.

[9]刘佳，杨士莪，朴胜春.基于EEMD的地声信号单通道盲源分离算法 [J].哈尔滨工程大学学报，2011，32（2）：194-199.LIU JIA，YANG SHI′E，PIAO SHENGCHUN.The Single Channel Seismic-acoustic Signal Blind Source Separation Method Based on EEMD [J].Journal of Harbin Engineering University，2011，32（2）：194-199.

[10]MA HONGGUANG，JIANG QINBO，LIU ZHIQIANG，et al.A novel blind source separation method for single-channel signal[J].Signal Processing，2010，12（90）：3232-3241.

[11]TZAGKARAKIS G，PAPADOPOULI M，TSAKALIDES P.Singular Spectrum Analysis of Traffic Workload in a Large-Scale Wireless LAN [C].CDROM of Proceeding MSWIM′07，Chania，Crete Island，Greece，October 22-26，2007.

[12]CICHOCKI S A.自适应盲信号与图像处理 [M].吴正国，译.北京：电子工业出版社，2005.CICHOCKI S A.Adaptive blind signal and image processing [M].WU ZHENGGUO Translated.Beijing：Publishing House of Electronics Industry，2005.