载人小行星探测轨道设计
武江凯 王开强 张柏楠 白明生 李志海
(中国空间技术研究院载人航天总体部,北京100094)
1 引言
小行星是太阳系内类似行星环绕太阳运动,但体积和质量比行星小得多的天体。长期以来,针对小行星的无人探测大多是对小行星表面物理、地质特征 (如形状、大小、质量分布等)进行观测或取样研究,由于航天员具有主观能动性,可以进行现场考察、科学仪器的布置、样本采集和样本初步辨识等探测活动,因此可以更好地完成小行星的探测任务。同时由于近地小行星还存在撞击地球的威胁,如果通过载人探测可以对其轨道进行偏移,将使地球免遭一场劫难。因此,对小行星进行载人探测意义重大[1]。
截止到目前,人类共对小行星进行了7次探测,全部为无人探测,其中3次为飞掠探测。最近一次探测为2003年5月发射的日本 “隼鸟号”探测器,对小行星 “丝川”进行探测,采集了小行星样本,并于2010年6月成功返回。中国月球探测器 “嫦娥二号”也将在2012年年底或2013年年初对一颗对地球具有潜在威胁的4179号小行星进行飞掠探测。理论上,文献[2]对2029到2036年间Apophis小行星探测任务进行了初步设计和分析,文献[3]提出了使用 “猎户座”飞船探测小行星的计划,并对探测方案进行了初步设计。
目前我国在载人小行星探测领域的研究还处于空白,但是小行星探测已经逐渐成为航天大国载人深空探测的发展趋势,根据我国载人航天的长远规划,有必要提前对未来的探测任务作出初步研究。本文以载人小行星探测为背景,主要从任务分析的角度出发,对载人小行星探测轨道设计方法进行研究,对发射窗口在2045年的编号为89136小行星(以下称小行星A)进行探测轨道设计,并对任务中止轨道特性进行分析。
2 轨道设计基本条件
(1)约束条件
根据我国目前航天技术发展现状,本文对发射窗口、总飞行时间和再入地球大气速度ventry提出了约束要求如下:
1)发射窗口在2020-2050年之间。
2)飞行时间不大于200天。目前,国际空间站上的航天员轮换周期约为170~180天。本文考虑20~30天的余量,认为200天之内是航天员可以承受的飞行时间。
3)根据文献[2-3],按照目前的再入技术发展状况,暂定载人探测器的再入速度不超过12km/s。
此外,通常还存在再入角的约束要求,即返回舱再入大气的再入角需要控制在一定范围之内。但是,载人小行星探测中,可以通过调整返回舱进入 “地球影响球”时的速度矢量距地心的距离,来控制再入角的大小,以满足再入要求,在本文轨道设计中未涉及,故不将其列为约束条件。
(2)基本假设
1)由于小行星体积、质量都比较小,故可忽略它对探测器的引力作用。
2)共面假设:在本研究中,候选的目标小行星的轨道倾角较小(主要候选星小于3°,备选目标星不超过5°),因此假定小行星在黄道面内。
(3)设计变量
本研究中的设计变量包括发射窗口、速度增量和飞行时间。其中发射窗口和飞行时间是自变量;速度增量是因变量,它可以根据发射窗口和一定的飞行时间进行相关轨道设计计算得到。需要说明的是,本文所指的发射窗口是指从地球停泊轨道发射逃逸的时间,飞行时间是指从地球停泊轨道出发至返回再入地球大气的飞行时间,速度增量是指从地球停泊轨道上加速及以后的速度增量。
(4)坐标系定义
定义一个日心黄道惯性坐标系,坐标原点为太阳质心;X轴指向J2000.0平春分点;Y轴在黄道面内沿逆时针方向垂直于X轴;Z轴垂直于黄道面,其指向与X轴和Y轴满足右手定则关系。
3 轨道设计
Lambert问题,是二体问题中在给定时间内从一个位置转向另一个位置的通用的两点边界值问题。本文基于Lambert理论,对载人小行星探测轨道进行设计。
3.1 Lambert问题
根据Lambert理论,在中心引力作用下的二次曲线运动,从一点运动到另一点的转移时间,仅与轨道半长轴、两点之间距离和两点到引力中心的距离之和有关。其数学表述为

式中μ为中心体引力参数;Δt为转移时间;F为变量函数;a为转移轨道半长轴;ri,rf分别为中心引力体到转移始末点的距离;F为变量函数;c为初始和末态位置之间距离。进一步,假定转移轨道的初始和末态的位置矢量已经确定,则对于固定的转移时间Δt,可求出转移轨道的类型,进而得到在始末两点的速度矢量。在文献[4-5]中给出了开普勒轨道上始末两点位移和速度矢量关系为

式中ri、rf为中心引力体到转移始末点位移矢量;f、g为Lagrange参数;vi、vf为转移轨道上始末点速度矢量。定义两个普适变量则应用普适变量表示的状态转移矩阵中各Lagrange参数为
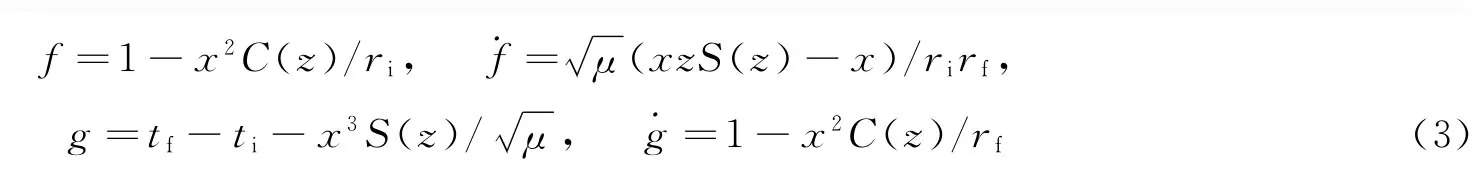
式中E=Ef-Ei表示始末位置处偏近点角差[4-5]。C(z)、S(z)为关于普适变量z的函数,对于椭圆 型 转 移 轨 道引入中间变量y=rirf(1-cosθ)/p,θ表示始末两点之间真近点角之差,p表示转移轨道的轨道半通径,则式(3)可以表示为

对比式(3)和文献[4]中应用经典轨道参数对Lagrange参数的描述,得到则应用普适变量表示的Lambert方程为

给定z一个较小初值,分别计算普适变量C(z)、S(z)、y、x,通过式(5)计算转移时间Δt1=tf-ti,并与给定的转移时间Δt进行比较,判断二者之差是否满足允许误差要求,如果不满足,则重复赋予z一个新值,重复以上过程,否则迭代结束,并依次求解4个Lagrange参数,应用式(2)则可以得到转移轨道上初始速度vi和末端速度vf分别为
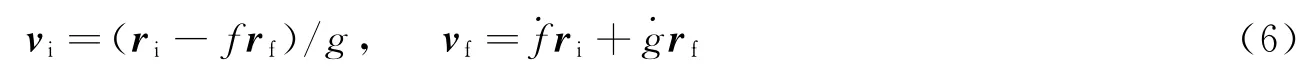
计算得到初始和末端速度后,根据开普勒轨道理论,计算得到飞行器在初始运行轨道和最后运行轨道(目标轨道)相应点的轨道速度v1和v2,则相应的速度增量为
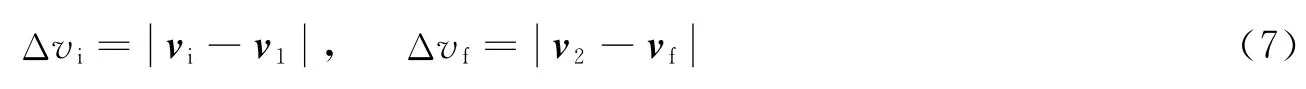
式中 Δvi为飞离地球时刻速度增量;Δvf为到达小行星时速度增量。返回轨道设计方法类似。对于从地球停泊轨道出发的飞行器,可以考虑在转移轨道近地点进行一次加速,将飞行器送入日心转移轨道[6]。
3.2 模型及设计方法验证
针对编号为2000SG344的小行星105天的载人探测,采用3.1节中计算方法,利用Matlab对利用本方法设计的转移轨道进行仿真计算,本文和NASA计算的速度增量比较如表1所示[1]。

表1 NASA/本文105天编号为2000SG344小行星载人探测的任务数据Tab.1 Crewed mission data of NASA/own about asteroid 2000SG344
分别对比表1中相对应的两列数据,发现其各段速度增量相差在0.01km/s量级,各节点时间相差在3天之内,总速度增量相差0.1km/s量级。
根据JPL星历,在STK中Astrogator模块下,对地球和编号为2000SG344的小行星轨道参数及探测器的初始状态进行定义,根据发射窗口,按照表1中本文计算的结果对探测器施加速度增量,得到的飞行轨道,且探测器可在预定的时间和区域与小行星交会,并返回地球,交会时刻探测器与小行星距离偏差为103km量级,说明所采用的基于Lambert问题的轨道模型的正确可靠。
综上所述,本文设计的轨道模型、计算方法及结果完全正确,满足初步轨道设计的要求,可以为载人小行星探测的概念研究提供支持服务。
3.3 小行星A的载人探测器轨道设计
对于载人小行星探测器的轨道设计,约束条件主要为速度增量、发射窗口、环境控制与生命保障系统设计能力,飞行时间及其分配,再入速度等,其中速度增量和飞行时间是制约探测器探测能力最直接的因素,同时二者又互相耦合,可以通过延长飞行时间 (任务周期)达到速度增量最小的目标,同时缩短飞行时间又直接引起速度增量的增大,所以对于中长期载人探测器,如何对飞行时间和速度增量进行综合考虑,使任务规模达到最小,显得至关重要。
本文从发射窗口、飞行时间、速度增量综合衡量,以发射窗口t0、出发段时间Δt1、返回段时间Δt2为设计变量,系统任务总质量M=m1+m2+m3为优化目标,其中航天员消耗质量m1=(Δt1+Δt2)mA,推进剂消耗质量m2=m3(eΔv1(Δt1,t0)+eΔv2(Δt2,t0)-2),m3为系统结构质量,mA为航天员每日消耗质量,Δv1(Δt1,t0)表示出发段速度增量为关于 Δt1、t0的函数,Δv2(Δt2,t0)表示返回段速度增量为关于Δt2、t0的函数。推进剂消耗量计算过程中不考虑系统结构质量变化和航天员消耗质量对系统结构质量的影响。以任务总质量M最小为目标进行优化选择,优化过程在此不再赘述。对小行星A探测任务优化结果为:发射窗口t0为2045年5月27日,飞行时间为Δt1=127天、Δt2=21天。应用3.1节中设计方法,对小行星A载人探测器转移轨道进行设计,转移轨道参数及各飞行段速度增量和飞行时间如表2所示,且再入地球大气层速度ventry满足小于12km/s的约束。

表2 载人探测小行星A的151天的速度增量及转移轨道要素Tab.2 Speed increment and orbital elements of transfer orbit for 151days crewed mission to asteroid A
小行星A的151天载人探测任务的转移轨道如图1所示,其中AU为天文单位,1AU=1.496×108km。
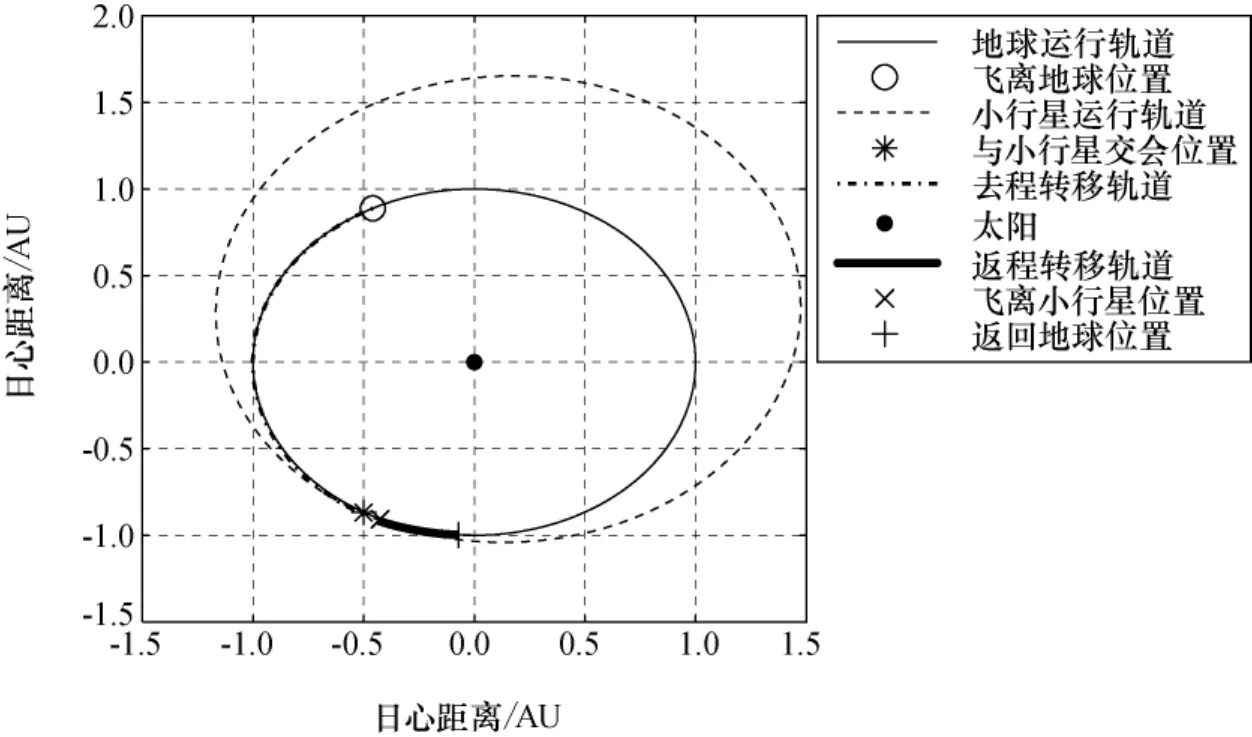
图1 载人探测小行星A的151天任务轨道Fig.1 Trajectory of 151days for crewed mission to asteroid A
4 任务中止轨道特性分析
任务中止轨道是指当探测任务执行过程中,由于意外故障事件,探测器系统能够通过轨道机动或巡航,安全再入地球的轨道。本文以小行星A探测任务为例,仅考虑在探测器故障模式下,对其直接返回中止轨道特性进行初步讨论分析。
载人小行星探测任务中,大部分时间集中在地球—小行星日心过渡飞行段和小行星—地球日心返回飞行段,所以不考虑在发射过程中逃逸救生和再入过程中结构防热问题。其中,在小行星—地球日心返回飞行段,由于探测器采用直接再入大气层模式,不再进行轨道机动,即使探测器发生故障,只要GNC分系统 (包括手动操纵系统)可以正常工作,探测器就可以安全返回地球。因此本文重点对地球—小行星日心过渡飞行段中探测器发生故障时,任务中止轨道特性进行分析。
任务中止轨道设计受到很多方面约束,任务中止时施加的速度增量、任务中止后返回地球所花费的时间及地面测控条件是任务中最重要的3个约束,在本文中主要考虑前两个约束。当探测器的推进分系统发生故障时,可使用的速度增量成为最主要约束,当环境控制与生命保障分系统发生故障时,最短的返回时间成为最主要目标。其中,当推进系统发生故障时,若故障模式为燃料泄漏,则可根据泄漏程度决定是否对任务轨道做出调整;若为其他故障模式,则需要在转移轨道中进行巡航,等待地面发射新的推进舱与探测器进行对接,将其 “拖”回地球。此处主要对以上两种故障情况下任务中止轨道特性进行分析。
由表2可知,在第一次轨道转移后,探测器还具有6.648km/s的推进能力,因此可将此剩余推进能力作为约束,以返回时间最短进行寻优得到以下规律:
1)当设定返回时间一定时,故障发生的时间越早,其返回所需的速度增量越小,若将任务中止后直接变轨返回时间设定为20天,从地球出发时开始,故障发生在不同时刻所需的速度增量变化如图2所示 (计算方法参见本文3.1节),但其最大变轨速度增量为2.864km/s,远小于剩余的6.648km/s的推进能力。
2)当假定发生故障的时间为一定时,对探测器在不同返回时间里的速度增量变化情况研究发现:随着返回时间的增加,所需的速度增量逐渐变大。若将故障发生时刻与出发时刻间隔 (以下简称故障时间)设定为50天时,其返回所需速度增量如图3所示 (计算方法参见本文3.1节),可以看出,对于故障时间为50天的任务中止,探测器满足1.5天返回的要求。
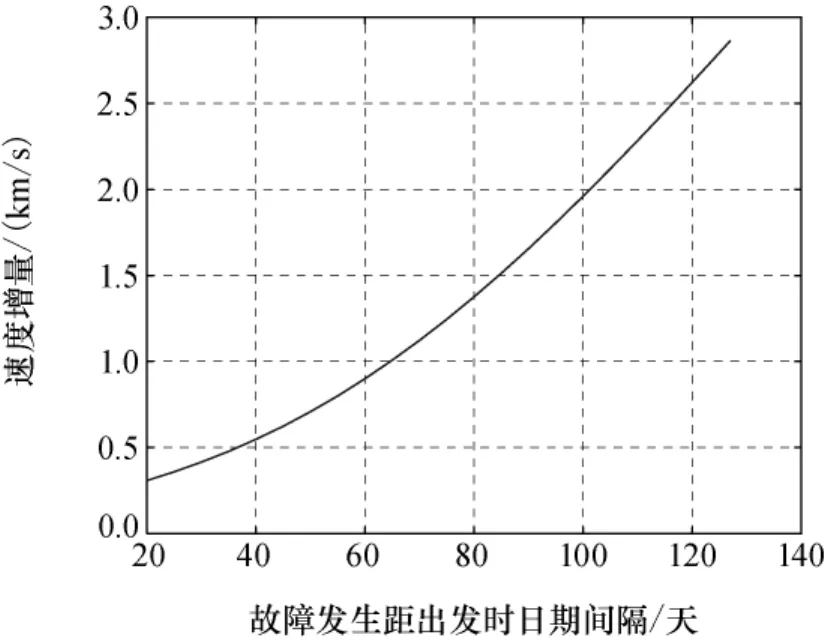
图2 速度增量与故障发生时刻的关系Fig.2 Relation curve of speed increment and failure dates

图3 速度增量与返回时间关系Fig.3 Relation curve of speed increment and return time
基于上述分析,综合考虑故障时间和任务中止后返回时间,得到以下结论:
1)若推进系统正常,环境控制与生命保障系统发生故障,需在最短时间内返回地球,则有:对于故障时间少于60天的飞行任务,可选择飞行时间最短为1.8天,速度增量为6.648km/s返回地球;对于故障时间大于60天的飞行任务,以6.648km/s速度增量返回,飞行时间最短为7.4天。
2)若环境控制与生命保障系统正常,推进系统发生故障,需要以最小速度增量返回地球,则有:对于故障时间大于20天的飞行任务,在既定剩余任务时间内进行变轨飞行情况下速度增量最小;对于故障时间小于20天的飞行任务,其速度增量随着返回时间变化较小,综合考虑到飞行任务的安全性,可选择在与故障时间相同的时间内返回即t1=t2,且速度增量都不会超过6.648km/s。
综上所述,载人小行星探测任务中,推进分系统和GNC分系统应具有很高的可靠性。这样,在发生其他故障时,导致任务中止时,探测器应具有应急返回地球的能力,这对于保障航天员的安全性至关重要,对于整个探测任务也意义非凡。
5 结束语
文章应用普适变量法求解Lambert问题,完成了基于二体问题的载人小行星探测轨道初步设计,但实际上载人深空探测轨道是非常复杂的,需要采用精确的动力学模型,并进一步根据实际情况对轨道修正、导航、制导与控制等技术进行研究。
对两种故障情况下任务终止轨道特性分析,故障发生时刻越早,所需速度增量越小;返回时间越长,所需速度增量越小。在故障发生时刻较晚,同时考虑探测器原有设计能力的情况下,需要在较短时间内返回,则推进分系统必须具有高可靠性,提供相应速度增量。
[1]FARQUHAR W ROBERT,DUNHAM W DAVID,MCADAMS V JIM.Near-Earth Asteroid Rendezvous(NEAR)Mission Overview and Trajectory Design [J].Journal of the Astronautical Sciences,1995,43:353-371.
[2]ZIMMERMAN DANIEL,WAGNER SAM,WIE BONG.Preliminary Design of a Crewed Mission to Asteroid Apophis in 2029-2036 [C].AIAA:2010-8374,2010.
[3]HOPKINS B JOSHUA,DISSEL F ADAM.Plymouth Rock:Early Human Missions to Near Earth Asteroids Using Orion Spacecraft[C].AIAA:2010-8608,2010.
[4]ASHISH TEWAIR.Atmospheric and space flight[M].New York:Birkhauser Boston,2006.
[5]李亮,和兴锁,张娟,等.普适变量法在深空探测器轨道设计中的应用 [J].西北工业大学学报,2004,22(6):744-747.LI LIANG,HE XINGSUO,ZHANG JUAN,et al.Application of universal variables to designing deep-space probe orbit[J].Journal of Northwestern Ploytechnical University,2004,22(6):744-747.
[6]乔栋,崔祜涛,崔平远,等.小行星探测最优两脉冲交会轨道设计与分析 [J].宇航学报,2005,26(3):362-367.QIAO DONG,CUI HUTAO,CUI PINGYUAN,et al.Design and analyze optimum two-impulse transfer trajectory for exploring asteroids[J].Journal of Astronautics,2005,26(3):362-367.

