倒虹吸管身段压强数值模拟研究

何照青，陶洪飞，牧振伟，李 娟，李 新

（1.水利部新疆水利水电勘测设计研究院，乌鲁木齐830000；2.新疆农业大学水利与土木工程学院，乌鲁木齐830052；3.新疆额尔齐斯河流域开发工程建设管理局，乌鲁木齐830000）

倒虹吸是穿越山谷、河流、洼地、道路或其他障碍物时常采用的水工建筑物，是利用当地大气压力进行工作的一种压力输水管道［1-2］。大型倒虹吸具有输水流量大、倒虹吸管身段长、进出口允许水头值较小、规模空前以及投资巨大等特点，探究其合理布置和运行方式，揭示大型倒虹吸工程特有的水流特性问题，具有重大的工程意义［3-6］。

20世纪90年代以来，我国缺水城市的范围不断增大，严重程度不断加剧，缺水已严重影响我国经济的可持续发展，其中以新疆最为严重。新疆干旱少雨，对长距离输水的要求比较高，北部有一大型供水工程——小洼槽倒虹吸，该工程是目前国内较大、较难、较长的引水工程。小洼槽倒虹吸工程全长5766m，最大静水压力水头46m，最大水头损失4.328m，引用流量17.5m3/s；倒虹吸为DN3100输水管，管道长度5136m。文章主要通过采用标准k～ε模型模拟湍流，对小洼槽倒虹吸管身段进行三维流场数值模拟，对比原型实测数据和数值模拟计算的结果，为倒虹吸的运行提供可靠的依据［7-9］。

1 数学模型

标准k～ε模型［10-13］是由Launder和Spalding提出的，因其考虑了平均流动中的旋转及旋流流动情况，可以更好地处理高应变率及流线弯曲程度较大流动，使得标准k～ε模型具有稳定性、经济性、计算精度较高和基本形式较简单等优点，因此，采用标准k～ε湍流模型。

标准k～ε湍流模型包括以下方程：

连续方程：

动量方程：

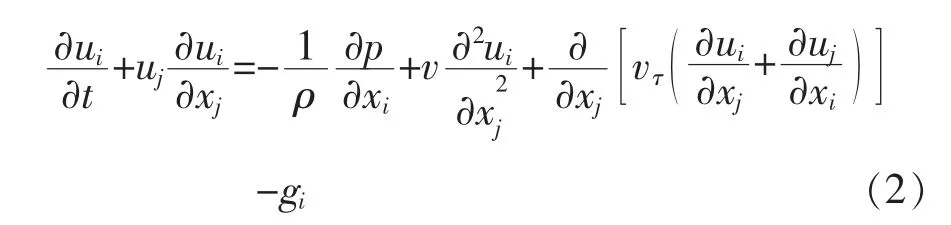
紊动能方程（k方程）：

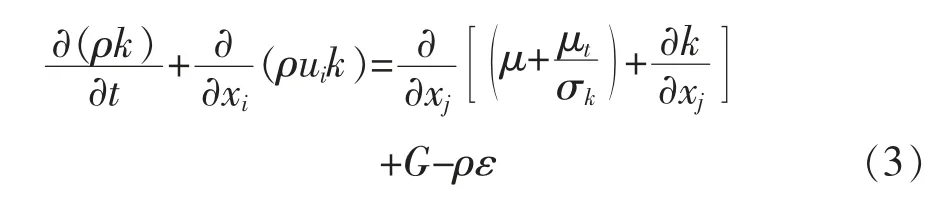
紊动能耗散率方程（ε方程）：

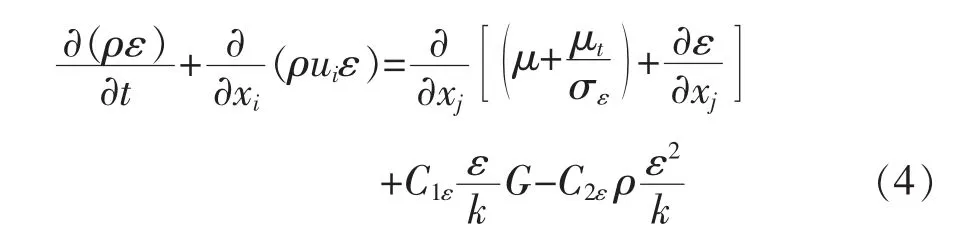
式中 σk和σε分别为k和ε的紊流普朗特数；C1ε和C2ε为ε方程常数；G为平均速度梯度引起的紊动能产生项；ρ和μ分别为体积分数加权平均的密度和分子粘性系数，可由紊动能k和紊动耗散率ε求出：

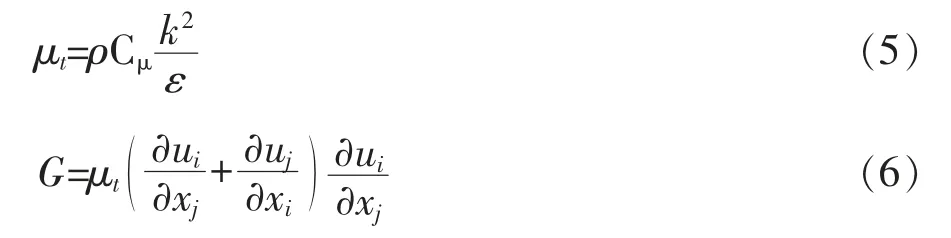
式（5）中 Cμ为经验系数；式（6）中，i=1，2，3，即{xi=x，y，z}，{ui=u，v，w}；j为求和下标；方程中通用模型常数［14］Cμ=0.09，C1ε=1.44，C2ε=1.92，σk=1.0，σε=1.3。

采用有限体积法对控制方程组进行离散，数值计算采用基于同位网格的SIMPLE法。

2 网格划分及边界条件

由于倒虹吸是轴对称结构，因此对倒虹吸取半结构进行了划分，这样既减少网格的数量，又节约了存储空间，还可以加快计算速度。对倒虹吸管道进行数值模拟，在不同流量下了解流场特性，倒虹吸模拟区域为：顺水流x 方向桩号0+170.40～5+672.49m；沿水深y方向高程549.36～592.62m，选取高程582.83m为基准高程；沿宽度z方向0～10.93m。倒虹吸进口节制闸段与前池段的几何边界较规则，因此采用六面体结构网格进行网格划分，而进口段的几何边界不规则，则布置为四面体非结构网格。为获得精确数据观察流场特性，对进出口段进行局部网格细化，计算区域网格数约13.02万个，网格划分如图1所示。

倒虹吸管边壁、渐变段、连接段、进水口和出水段均为固壁，其边界条件按固壁函数处理，壁面处为无滑移边界，对靠近壁面区域则采用标准壁面函数法来处理。渐变段、连接段和进口处的自由液面在同一水平面上，即在自由表面上可认为垂向速度为零。

图1 计算区域网格划分

3 计算结果

通过计算流体力学软件FLUENT对水流运动进行数值模拟，得到倒虹吸模拟区域的沿程断面压强。分别选取Q=12m3/s、Q=14m3/s两种基本工况与实测数据进行验证，这样选取的结果更具有特殊性和代表性。

3.1 数值模拟计算结果

对小洼槽倒虹吸进行了压强大小的数值模拟计算，对Q=12m3/s和Q=14m3/s两种流量下计算其观测断面（AP2、AP4、AP6、AP8、AP10、AP12、AP14）的压强值，其观测断面压强分布如图2、图3所示。

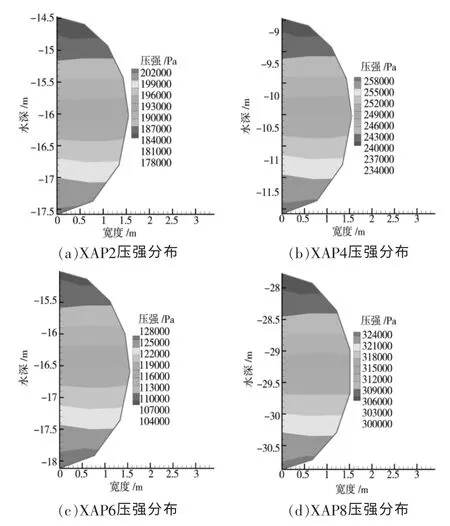
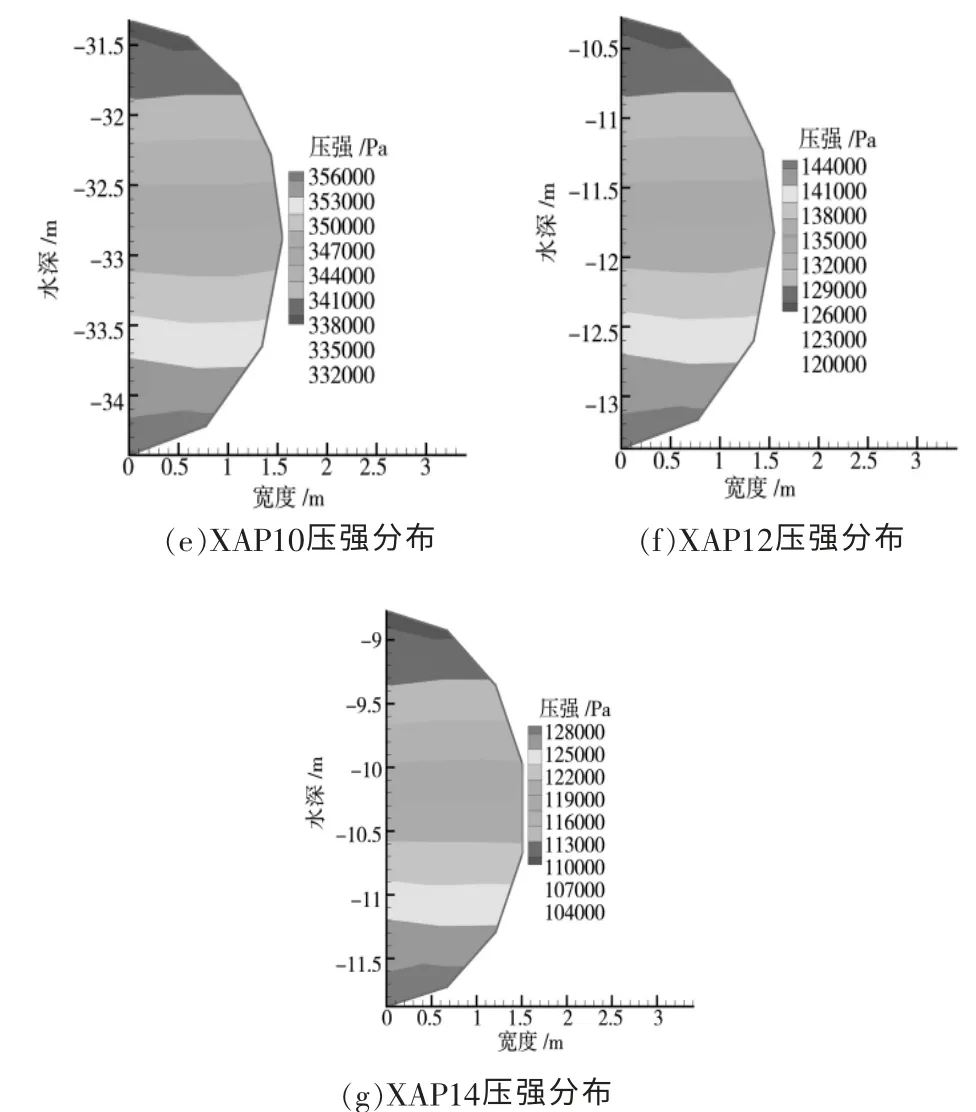
图2 在流量Q=12m3/s下各观测断面压强分布

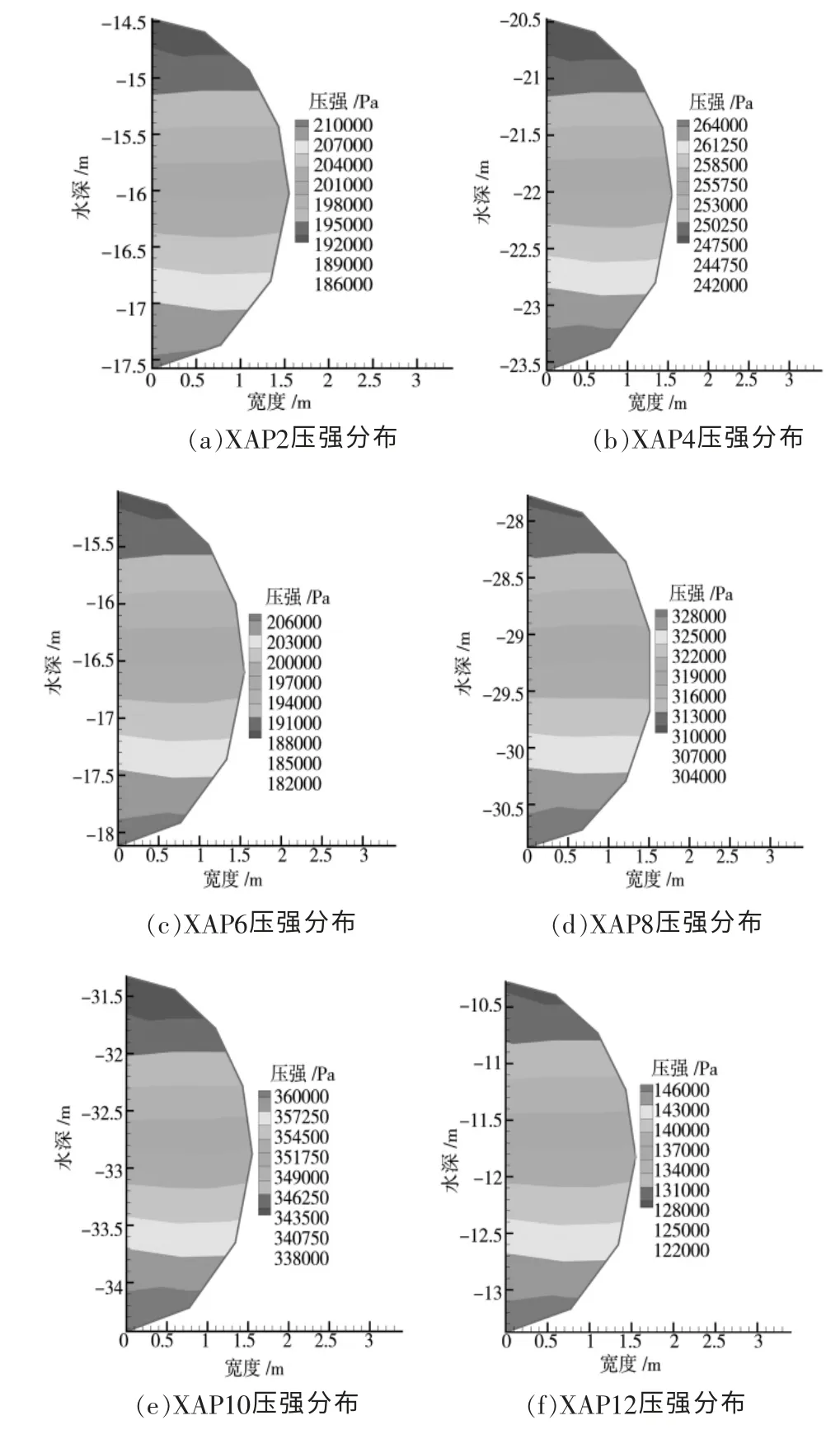
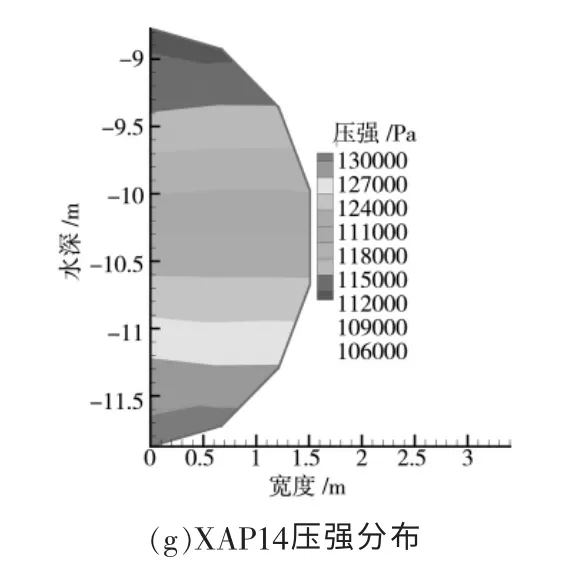
图3 流量Q=14m3/s下各观测断面压强分布

由图2（a）～（g）可知：

（1）每个监测断面的压强最大值发生在管道底部，最小值是在管道顶部。

（2）随着管线的逐渐延长，断面压强值增大，在倒虹吸管道的最底端（即XAP10监测断面，桩号为3+436），管道压强达到最大值0.356MPa，这时管道顶部的压强为0.332MPa，满足管道压力荷载。

（3）管段最小压强发生在倒虹吸出口处（即XAP14监测断面，桩号为5+412）管道压强最大值0.128MPa，这时管道顶部的压强为0.104MPa。

（4）各个监测断面压强分布为从上到下逐渐递增的形式。

由图3（a）～（g）可知：

（1）每个监测断面的压强最大值发生在靠近管道底部的位置，最小值是竖直方向靠近管道顶部。

（2）随着管线桩号的逐渐变大断面压强值增大，在倒虹吸管道的最底端（即XAP10监测断面，桩号为3+436），管道压强达到最大值0.360MPa，这时管道顶部的压强为0.338MPa，在管道压力承载范围内。

（3）管段最小压强发生在倒虹吸出口处（即XAP14监测断面，桩号为5+412）管道压强达到最大值0.130MPa，这时管道顶部的压强为0.106MPa。

（4）各个监测断面压强分布规律比较明显。

综上所述，数值模拟计算各流量下断面压强的大小，在监测断面取断面的面平均值，在流量Q=12m3/s和Q=14m3/s下各断面的压强大小值如表1所示。

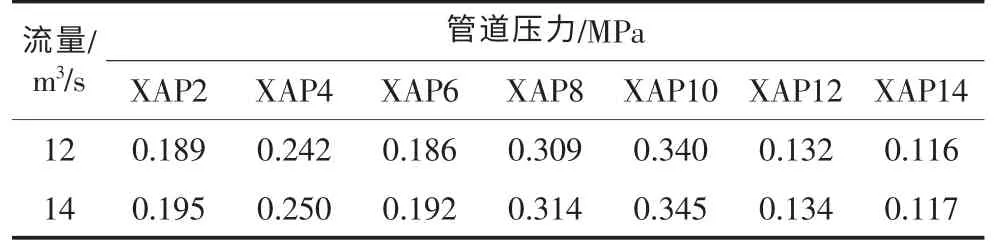
表1 小洼槽倒虹吸管身段压力计算值

3.2 实测数据

布置的监测项目包括：管道内水脉动压力观测、管道时均压力观测、管道接头变形观测、管道径向变形、进出口结构变形观测、进口镇墩应力应变及温度观测、管道渗漏观测等监测项目。本文主要对管道内水脉动压力进行研究，工程运行过程中，在流量Q=12m3/s、Q=14m3/s两种基本工况下实测数据见表2。

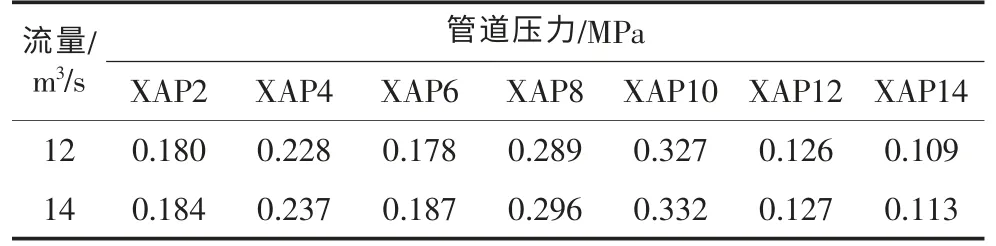
表2 小洼槽倒虹吸管身段压力实测值

3.3 对比分析

实际工程中压强是一项很重要的指标，决定着倒虹吸管道的设计荷载，同时，在压强较大的地方容易对管壁发生破坏现象。表3为倒虹吸管身段实测资料与数值模拟计算的压强大小值对比，从表3可知，实测数据与数值模拟计算数据均能反映断面压强变化情况，而且两者误差较小，结果与实际工程现象比较吻合。

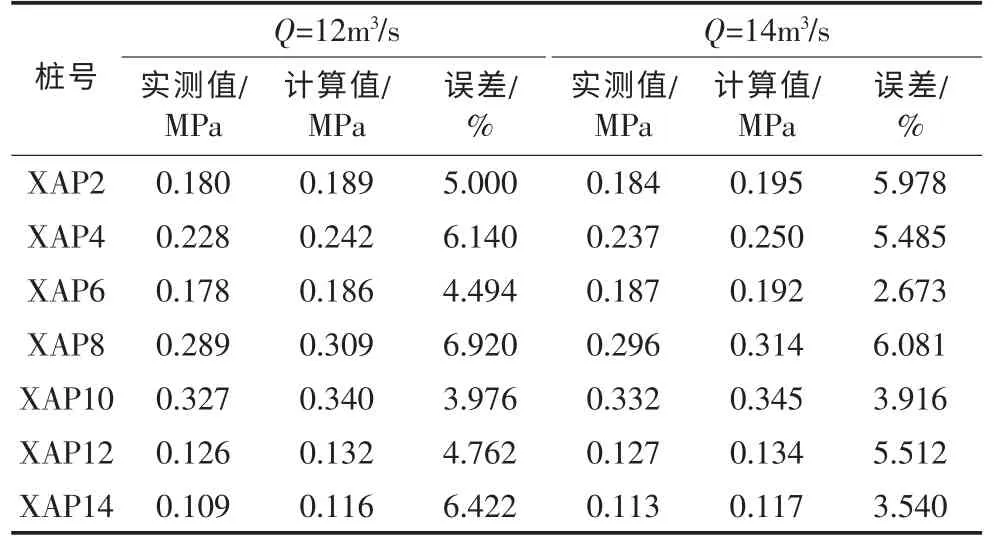
表3 小洼槽倒虹吸管身段实测资料和数值计算压强对比

4 结语

（1）利用非恒定流标准k～ε模型对倒虹吸不同流量下管身段压强进行了模拟，并将计算结果与实测值进行了比较，结果表明数值模拟结果比实测资料略微偏大，总体上吻合较好。

（2）对不同流量下的各监测断面的压强分布进行了分析，发现压强大小由上至下逐渐递增，而且管身段压强随着桩号的增加而增加（从进口段到管线的最低点），最大压强发生在管线的最低点，模拟所得结果与实际工程中现象吻合，为倒虹吸的运行管理提供理论依据。

［1］余际可，罗尚生，田文铎.倒虹吸管［M］.北京：水利电力出版社，1989.

［2］李惠英，田文铎，阎海新.倒虹吸管［M］.北京：中国水利水电出版社，2006.

［3］宋天文，邱勇.高水头倒虹吸管流量控制试验研究［J］.人民长江，2008，39（16）:85-86.

［4］侯晓红.潮白鹤倒虹吸输水流量计算方法探讨［J］.水科学与工程技术，2005（2）:9-11.

［5］李娟，韩明轩，牧振伟，等.倒虹吸工程水力学模型试验［J］.南水北调与水利科技，2012，10（4）:73-75.

［6］何照青，牧振伟，李娟，等.基于VOF模型的倒虹吸进出口流场数值模拟［J］.中国农村水利水电，2012（3）:94-97.

［7］石泉，张立德，李红伟.大型倒虹吸工程设计与施工——大口径、高压力预应力钢筒混泥土管与玻璃钢管在倒虹吸工程中的应用［M］.北京：中国水利水电出版社，2007.

［8］李国栋，李建中，许文海，等.大型倒虹吸管充水过程的数学模型与计算［J］.武汉大学学报（工学版），2007，40（2）:12-16.

［9］葛毅.虹吸管道内流场的数值模拟和试验研究［D］.湖南:湖南大学，2007:61-62.

［10］王福军.计算流体动力学分析——CFD软件原理与应用［M］.北京:清华大学出版社，2004.

［11］韩占忠，王敬，兰小平.FLUENT流体工程仿真计算实例与应用［M］.北京：北京理工大学出版社，2004：19-20.

［12］江帆，黄鹏.Fluent高级应用于实例分析［M］.北京:清华大学出版社，2008.

［13］张凯，王瑞金，王刚.Fluent技术基础与应用实例［M］.北京:清华大学出版社，2010:2-3.

［14］SPEZIALE C G，THANGAM S.Analysis of an RNG based turbulence model for separated flows［J］.Int.J.Engng.Sci.，1992，30（10）:1379-1388.