水流数值模拟在滞洪区中的应用

刘晓琴，刘 伟，和宛琳

（河南省水利勘测设计研究有限公司，郑州450016）

水流数值模拟是将水流问题用数学方程进行描述，并在一定的定解条件下求解方程，从而模拟出某个理论或工程实际问题的水流状况。洪水演进方法可分为水文学方法和水力学方法。水文学方法有马斯京根法、特征河长法和水库调洪演算法等；水力学方法分为恒定流和非恒定流两种水流状态，恒定流模拟有河道水面线模型；非恒定流模拟有一维模型和平面二维模型。一维数学模型基本能满足大多工程的实际需要，在理论和实践上都比较成熟。平面二维数学模型正处于迅猛发展过程之中，在许多工程实际应用中已显示其技术优势［1］。

建设项目穿越（跨越）滞洪区时，可能对滞洪区行蓄洪水造成一定影响，同时滞洪区行蓄洪水时也将对建设项目产生一定影响，对滞洪区行蓄洪水过程进行全面模拟，将会为建设项目提供设计依据。蓄滞洪区内地势低洼，行蓄洪水时对洪水具有明显的滞蓄作用，水流具有明显的纵向和横向流特性，所以传统的一维恒定、非恒定流计算方法将不满足要求，二维非恒定流数学模型能够较准确地全面模拟计算域内水流的运动、水位的变化过程、冲淤情况等，以便更好地反映实际情况。

1 二维非恒定流数学模型

对于宽浅河道和以坡面流为主的宽浅型水域，水流具有明显的纵向和横向流特性，采用平面二维运动方程可较好地反映这类流场中水流运动特征，解决宽浅水域的水力计算问题。

二维非恒定流数学模型可全面模拟计算域内水流的运动、串流过程，能较准确地模拟、预测在修建工程前后计算域内洪水演进、串流淹没及建筑物过流状况。

1.1 模型基本控制方程

二维非恒定流数学模型基于圣维南（St.Venant）方程，主要由水流连续方程和动量方程组成［2］。

水流连续方程：

水流动量方程：

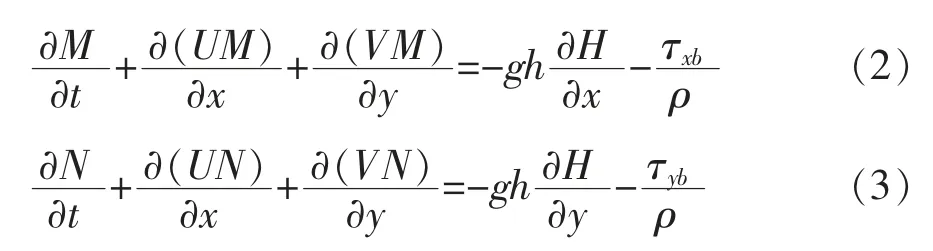
（1）从外部空间来看，园区位于古城区东部，其与外部连接的交通非常发达。高速公路、铁路、水路及航空网使苏州工业园区与外部畅通无阻。依靠发达的轨道交通，可以实现20 min到上海、60 min到南京，从而实现与上海、南京、杭州同城轨道化生活。此外，苏州市新制定的城市规划中，明确了苏州工业园的“苏州新城”地位，未来将成为长三角地区重要的经济和文化活动中心之一。

1.2 模型参数分析

二维非恒定流数学模型模拟计算基础数据通过实测地形图概化而得，需要确定的参数为糙率即洪水演进过程中的摩阻力。糙率应是水流和河床相互作用过程中，反映河道的边界粗糙程度、河床形态、含沙量浓度等所有影响水流阻力因素的综合系数。二维糙率涉及到岸、滩、槽的各细部，有时各细部糙率有较大差异。对于二维糙率问题，目前的处理方法：①先考虑一维情况下的综合糙率，然后在此基础上考察糙率沿河宽的变化；②考察谢才系数c沿河宽分布的规律，然后由曼宁公式得到糙率沿河宽的分布。

1.3 初始条件及边界条件

1.3.1 初始条件

对于给定的计算区域，在时间t=0时，令

1.3.2 边界条件

（1）进口边界条件。给出进口开边界处的水位过程，开边界上已知水位或流速分量及流量，一般根据计算区域的产汇流模型计算或由实测水文资料计算确定。

（2）出口边界条件。出口开边界有两类。一类是自然开边界，主要是经下边界或侧边界出流的河流，可按实测水文资料（水位～流量关系）确定。如无实测资料，则按附近河道纵坡，以均匀出流考虑。另一类是修建在下边界上的过水建筑物如铁路桥、涵，需按相应的桥、涵泄流公式进行控制。

（3）计算区域内过水建筑物的处理。如果计算区域内有横贯全区的阻水建筑，其中过水部分也可分为两类。一类是过水断面较大，可以做为自然过流考虑的穿渠河流；另一类是过水断面尺寸较小（或有压过流），如河渡槽、河倒虹等，泄水建筑物的泄流能力以相应的水力学计算公式计算，过流量则与建筑物上、下游流场耦合求解。

（4）陆地边界。根据流体固壁不可穿越的原理，在不考虑渗透的情况下，可认为陆地边界上法向速度为零；根据水流无滑动原理，水体在陆地边界上的切向流速也应为零。

2 模型应用实例

2.1 崔家桥滞洪区概况

崔家桥滞洪区位于安阳市以东10km的安阳县境内，南为安阳河，西为韩陵山，北为漳河，东为漳河故道。滞洪区沿67.00m等高线，北、东侧沿幸福渠及漳河故道修建围堤，南以安阳河左堤为滞洪区南部边界堤防，现状围堤残缺不全，长12.4km。当安阳河上游来水大于600m3/s时分洪，设计蓄滞洪水位65.75m，滞洪量0.61亿m3。滞洪区面积48.6km2，耕地0.42万hm2，涉及4个乡镇，72个村，现有人口7万人。分洪口门有2处，分别是曹马和郭盆口门。曹马口门位于安阳河左岸曹马村东，分洪口门宽1200m；郭盆口门位于郭盆闸上游772m，分洪口门宽500m。现状崔家桥蓄滞洪区仅通过梨园沟退水闸和下游安阳河无堤段退水进入安阳河。为减轻安阳河洪水压力，曾于1956年、1963年、1982年、1996年4次进洪，发挥了重要作用。滞洪区行蓄洪水时，洪水呈漫流状自然行洪，洪峰坦、历时长。

崔家桥蓄滞洪区洪水调度运用原则：安阳河流量小于600m3/s，不启用崔家桥蓄滞洪区；当安阳河发生20年一遇洪水时，河道流量1720m3/s，曹马分洪口向蓄滞洪区分洪620m3/s，曹马—郭盆闸河道泄量1100m3/s，此时需利用郭盆闸控泄600m3/s，郭盆分洪口向蓄滞洪区分洪500m3/s；当安阳河发生50年一遇洪水时，河道流量2300m3/s，曹马分洪口向蓄滞洪区分洪1200m3/s，曹马—郭盆闸河道泄量1100m3/s，此时需利用郭盆闸控泄600m3/s，郭盆分洪口向蓄滞洪区分洪500m3/s。

2.2 工程概况

石郑客运专线铁路桥南北向贯穿崔家桥滞洪区［3］，长8.17km，桥梁梁底板高程77.15～75.65m，设计滞洪水位65.75m，梁底板高于滞洪水位11.40～9.90m，铁路桥位于崔家桥曹马口门中间，桥上游口门宽733m，桥下游口门宽467m，口门总宽1200m。郭盆口门位于拟建铁路桥下游4.8km，远离铁路桥，工程不影响该口门分洪。

拟建锦州—郑州成品油管道工程从安阳县崔家桥乡杨辛庄东北500m处穿越幸福渠规划大堤进入崔家桥滞洪区［4］，途经和邵庄附近，从邢济村东北800m处穿安阳河左堤出滞洪区，滞洪区内管道长3.65km，穿越滞洪区采用开挖地埋方式。

2.3 二维非恒定流数学模型模拟

2.3.1 模型范围

以崔家桥滞洪区范围为界，北、东侧沿幸福渠及漳河故道修建围堤，南以安阳河左堤为滞洪区南部边界堤防，西为韩陵山。

2.3.2 模型网格剖分

采用1/10000地形图进行地形概化，剖分网格为正方形，间距为100m，计算区共7916个网格。崔家桥滞洪区三维地形图，地形等高线图（略）。

2.3.3 入流

入流点为滞洪区的郭盆、曹马分洪口门，入流采用两分洪口门的入流洪水过程线成果。

2.3.4 开边界

模型区内的石郑客运专线形成阻水中边界，按要求洪水不允许漫越铁路，因此铁路堤顶按不漫流处理；模型区内的成品油管道埋设于地面以下，对滞洪区行蓄洪水不产生影响。在滞洪区内部的其他阻水建筑物，如村庄房屋，堤防等，一般按当地地面加适当高度处理，不考虑溃决影响。模型四周按自由开边界处理。

经模拟计算，工程后崔家桥滞洪区50年一遇水深和流场矢量图（略），工程前后水位、流速对比见表1。

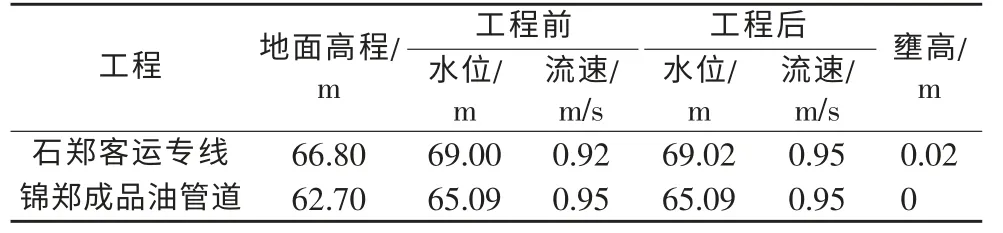
表1 工程穿越滞洪区段最不利情况计算成果

2.4 成果分析

2.4.1 石郑客运专线铁路桥

根据模拟计算成果，铁路桥建设后滞洪区水位最大壅高0.02m，在客运专线铁路桥范围内没有村庄，增加的淹没影响甚微。安阳河左岸有3个桥墩，位于崔家桥滞洪区曹马分洪口门处，分洪时正对桥墩，墩宽6.0m，将对水流有一定导流、分流作用，桥墩处水流较为紊乱，对工程附近的流势流态有一定影响；同时桥墩处最大流速由现状条件下0.92m/s增加至0.95m/s，对桥墩基础也产生冲刷影响。

2.4.2 中石油成品油管道

成品油管道穿越滞洪区时采用开挖方式，管道埋设于地面以下，建设项目对滞洪区分蓄滞洪运用等均不产生影响；而滞洪区分蓄洪水运用时于成品油管道处会产生一定的冲刷影响，根据模拟计算结果可知，在成品油管道沿线流速为0～0.95m/s，结合该处地质情况确定冲刷深度。

建设项目应根据分析计算结果，结合相应的规范规程，采用相应的工程措施，以减少防洪影响。

3 结语

滞洪区行蓄洪水时流态复杂、计算域大，建设项目穿越或跨越滞洪区时，行蓄洪水对建设项目的影响及建设项目对行蓄洪水的影响分析，采用二维非恒定流数学模型模拟计算，可以较为全面地模拟洪水演进、淹没及工程位置处流速状况等，为防洪评价提供评价依据［5］。模型实际运用过程中存在的主要问题有以下几点：

（1）二维非恒定流数学模型，必须有大量详实、完整的水文实测资料来支持。由于平面二维数学模型需要对地形资料进行概化，采用地形资料的精度和概化网格的大小直接影响洪水模拟的精度。特别是在河道部分，由于河道较小，而且不规则，对河道进行概化时难以用一个或多个网格描述，常常概化为规则断面，采用河道综合比降推算河道水位，河道概化的精度直接影响到河道设计洪水位的准确程度。

（2）模型边界条件确定常采用一维方法，由于平面二维模型计算的复杂性，在确定进出口边界和中边界时，需要很好地与二维水力条件相协调，但难以用实测资料来验证，给模型计算带来不确定性。

随着遥感、地理信息数据资料逐渐完善，二维数学模型也正处于迅猛发展过程之中，在南水北调总干渠左岸串流坡水区、漯河市沙北区等许多防洪工程实际的应用中已显示其技术优势，但模型仍有待进一步完善。

［1］李义天，谢鉴衡，等.河道平面二维泥沙数学模型研究及应用［A］.第二届全国泥沙学术会议论文集［C］.1995.

［2］李义天，赵明登，曹志芳.河道平面二维水沙数学模型［M］.北京：中国水利水电出版社，2001.

［3］河南省水利勘测设计研究有限公司.石郑客运专线安阳段特大桥防洪评价［R］.2007.

［4］河南省水利勘测设计研究有限公司.锦州—郑州成品油管道工程管线穿越河南省卫河流域滞洪区防洪评价［R］.2012.

［5］刘薇，彭新德，张小兵.一二维耦合水流数值模拟在防洪评价中的应用［J］.中国水运，2010，10（6）：112-113.

［6］陈辉.南水北调中线工程设计防洪水位研究［D］.南京：河海大学，2010.