空舰导弹纯方位目标指示综合仿真实验系统

孙 涛，谢晓方，唐 江，张龙杰

（1.海军航空工程学院 兵器科学与技术系，山东 烟台 264001；2.海军航空工程学院 研究生管理大队，山东 烟台 264001）

空舰导弹纯方位攻击是指仅根据目标方位信息，采取导弹自控飞行时间装定最小值，向目标初始方位发射导弹的攻击方式。这种攻击方式可以更好地适应复杂的电磁环境［1］和恶劣的信息条件。由于采用了被动探测设备，这种攻击方式也更有利于提高发射平台的隐蔽性。目前，美国的最新一代战机上均安装了被动探测设备［2－3］，主动雷达仅在必要时短时间开机；俄罗斯和以色列等国在这方面也有很强的技术实力。被动探测手段的重要性日益突出。

被动探测设备通常只具有测向能力，如何在这种条件下科学处理目标方位数据，利用空舰导弹有效进行目标搜索攻击，已成为航空武器系统与运用工程领域的热点问题。

在院校教学中，仿真实验有利于灵活配置实验内容，使理论教学和实践教学相融合［4－5］。为了使学生更好地理解纯方位目标指示数据处理的一系列模型和方法，有必要构建综合仿真实验系统，为准确、直观地研究纯方位目标指示条件下数据处理方法提供条件。

1 实验系统功能需求

仿真实验系统主要支持研究性实验，服务于探究性教学和实验比较法教学［6－8］，具备以下主要功能：

（1）支持主要的纯方位目标指示数据处理方法仿真，包括几何法、概率法、角速率法等，提供参数设置接口，实验用户可以自行修改目标、载机等参数；

（2）针对各类方法仿真结果，解算空舰导弹火控参数，支持目标捕捉概率的仿真计算；

（3）支持仿真过程记录和结果比对，满足实验教学与理论教学相结合的需求。

（4）提供模型开发接口，既能够为研究生等高级实验用户提供自定义仿真计算模型的实验条件，又支持本科生研究型实验，培养学生的创新意识和科研品质［9］；

2 主要仿真模型分析

2.1 几何法处理模型

几何法的基本原理与测向定位法（bearing－only，BO）［10－11］相同，通过在2个以上不同位置对目标方向的多次被动探测，解得目标的位置信息，从而为空舰导弹提供目标指示。设机载被动探测设备的最大探测距离为Rmax，目标方向指示的角误差为Δα，则目标指示为图1所示的虚线扇形区域。

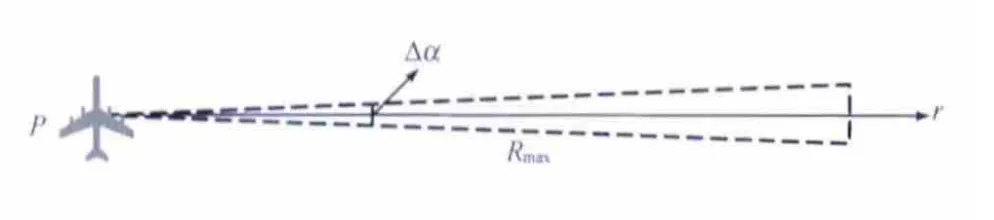
图1 基于被动测向的目标定位

在一定时间内对2个以上目标指示扇区的相交运算，可以为导弹计算出更加准确的目标区。随着探测次数的增加，目标区域不断缩小。通常情况下，在不同位置进行的被动探测很难做到同时进行，由此会在目标区计算中引入误差。先后在P1和P2两个不同位置进行被动探测的时间间隔为Δt，目标舰艇最大可能的机动速度为Vm，则误差补偿方法是将搜索区沿P2探测的正反方向分别延伸Δt·Vm，如图2所示。

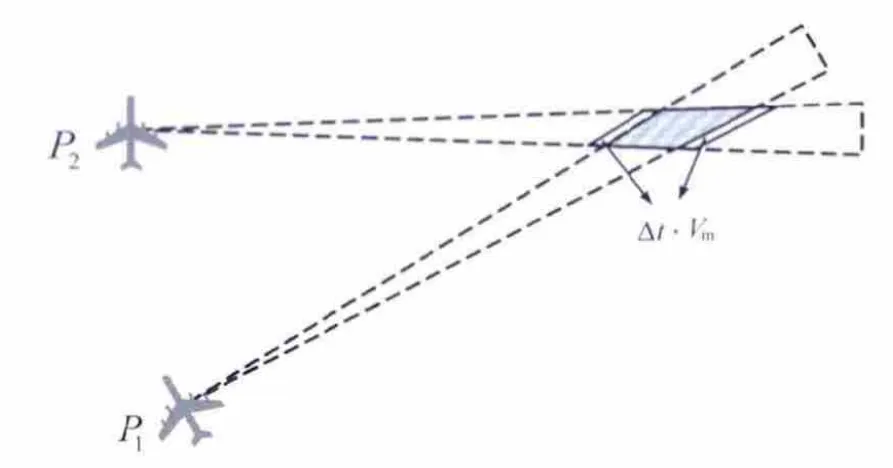
图2 测向时间间隔补偿

设导弹到达目标区之前的自控飞行时间为tZK，则期间舰艇的最大机动距离为tZK·Vm，补偿方法是按tZK·Vm将搜索区向外扩展［12］，如图3所示。

图3 导弹自控飞行时间补偿

2.2 概率法处理模型

载机在不同位置P1，P2，…，Pi，…，Pn，通过无源测向设备进行方位探测，分别得到目标相对于不同观测点的方位角φ1，φ2，…，φi，…，φn。通过以上信息估计目标位置。设目标T的真实位置为η＝（xT，yT），载机的测向点的位置坐标分别为（xp1，yp1），（xp2，yp2），…，（xpn，ypn），对于任意测向点pi（1≤i≤n），观测值为

δi是第i次测向误差。

设载机各次测向噪声不相关，为零均值，标准差为σi的随机噪声。表示方位角真值，则有），对于距离r的目标，φi的概率密度函数为：

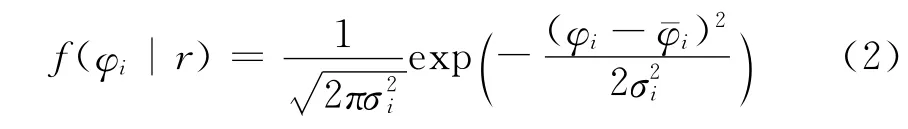
其中，Rmax为无源探测设备的最大探测距离，Rmin为无源探测设备的最小探测距离，则目标在探测区域的概率密度函数表示为：

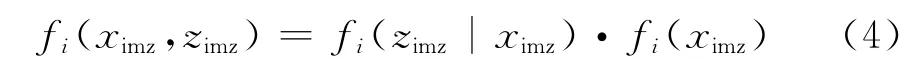
若对同一目标进行N次测量，各次测量相互独立，则联合概率密度函数为：

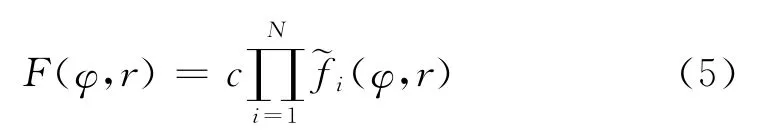
2.3 方位角速率法处理模型

本方法适用于纯方位目标的快速距离估计和定位误差估计，适用条件是在数据采集及处理期间载机保持平飞，并且被动传感器能够被目标连续照射。

假设载机与目标实际距离为r，载机飞行速度vP，载机方位指示分辨率εmax，将εmax视为载机对目标方位探测的量化单位。令Δn为单位时间Δt内载机的目标方位角示值变化量对应的量化单位个数。考虑到载机可能无法始终沿以目标点为中心的圆弧切向飞行，需要进行飞行方向补偿：

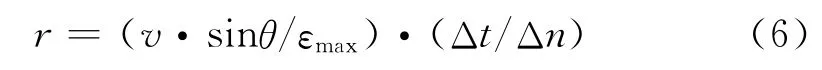
其中，θ为目标相对于载机飞行方向的方位角。该式表明，在已知载机飞行速度和载机方位指示分辨率的条件下，目标相对于载机的距离与方位示值变化率成反比关系。

对于空舰导弹，目标运动速度相对于载机速度很小，利用对称原理，视载机不动，而目标舰艇相对于载机以速度vP运动（见图4）。

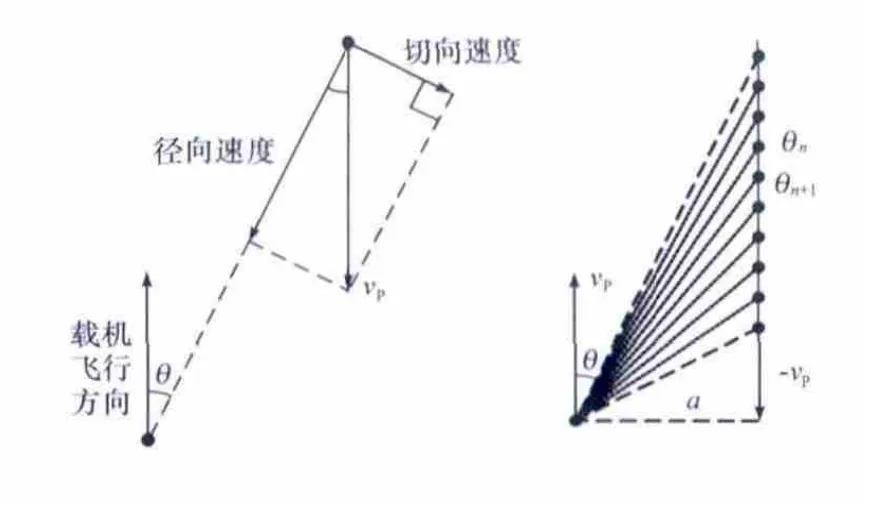
图4 载机－目标相对运动与目标方位测量

图中θ变化间隔为最小量化单位εmax，下标n为测量周期序号。

估计结果与方位示值变化周期的正确性和精度有直接关系。然而，载机上能够测得的只有各次测量之间的平均角速度，不能反映被测目标当前的实际角速度。相邻两测量时刻，目标方位角速度ωn，ωn＋1存在如下关系：

平均角速率比测量点当前实际值小，导致目标距离预测结果偏远。因此利用平均角速度作为目标距离估计的模型。

载机平飞条件下，如果把角速度看作目标方位角的函数，则有：

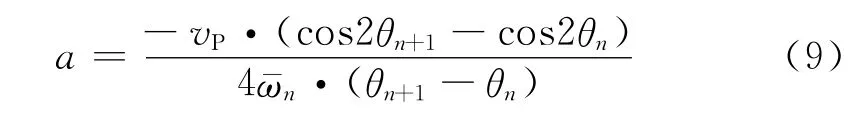
又因为，rn＋1＝a／cosθn＋1，所以，第n＋1次测量时，目标距离估计为：

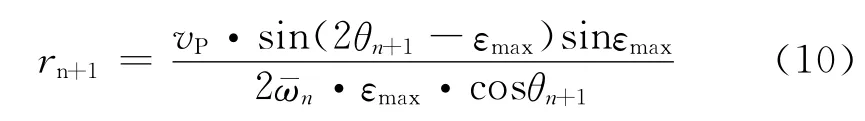
2.4 目标捕获仿真

在目标捕获概率方面，主要需考虑导弹进入搜索区的方向、自控终点的位置、所用的弹量，依照目标区内部目标概率密度分布情况进行积分求解（见图5）。而在仿真结果方面，则主要考虑对目标区的搜索覆盖率和用弹效费比。

3 仿真程序总体流程

综合仿真系统总体流程如图6所示。其中，几何法、概率法、方位角速率法计算模型作为开放资源预先存储，实验用户可直接调用，也可自行开发设计；初始仿真参数和导弹攻击参数可由用户设置。

图5 目标区搜索

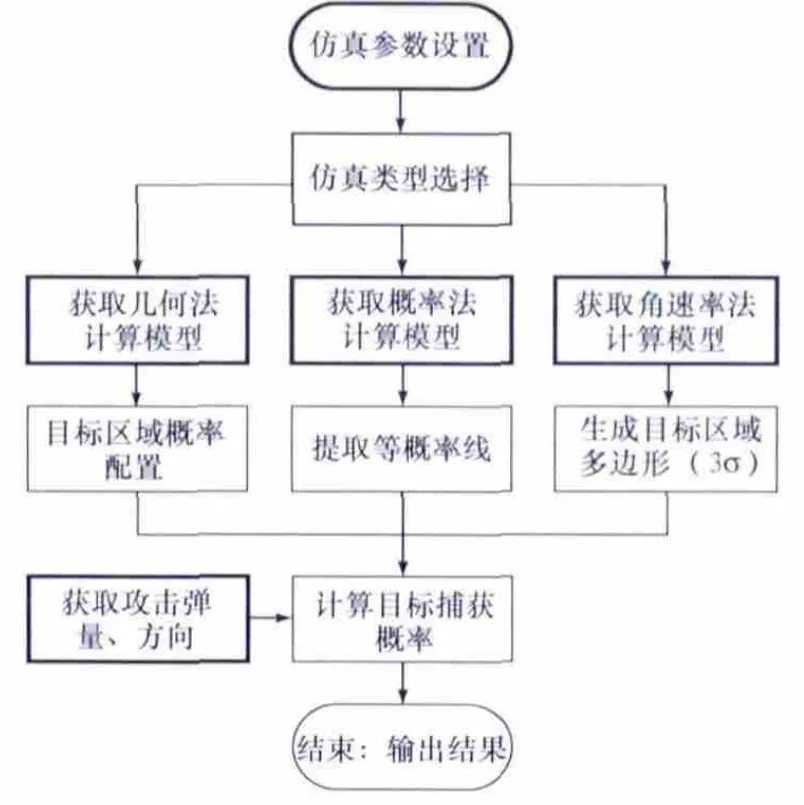
图6 载机纯方位无源定位算法流程图

4 部分仿真实验效果

4.1 几何法

设置被动探测角误差10°，载机运动速度为272 m／s，仿真结果如图7所示。图中飞机图标表示载机平台进行各次被动测向的位置，多边形表示经过多次探测之后，仿真计算得到的目标区。利用几何法得到的目标区可能是任意形状的凸多边行，也可提取如图所示的矩形目标区，同时可给出载机完成所有方位探测所需要的机动距离和飞行时间。

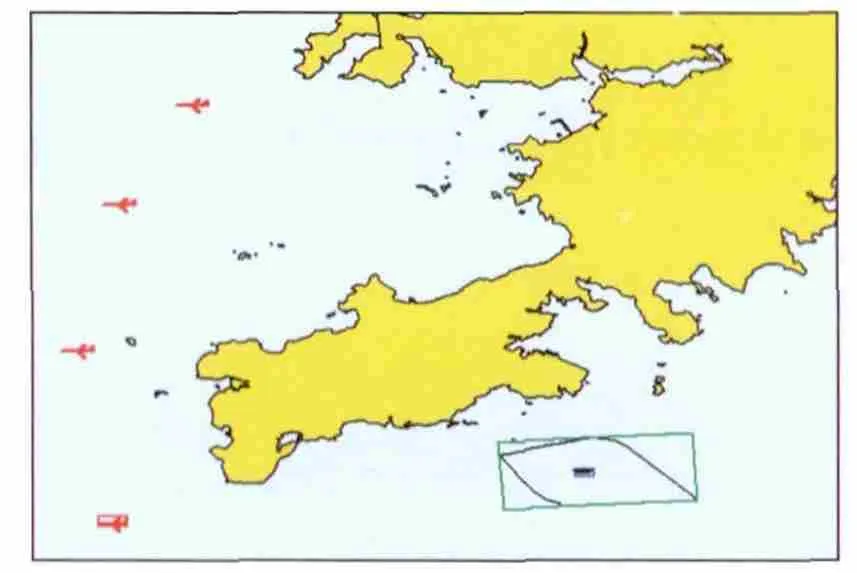
图7 提取的目标搜索区

4.2 概率法

选取载机初次探测位置为原点，φ＝0°，Rmax＝400 km，Rmin＝10km，δ＝3°，则单次测量目标概率密度分布如图8所示。

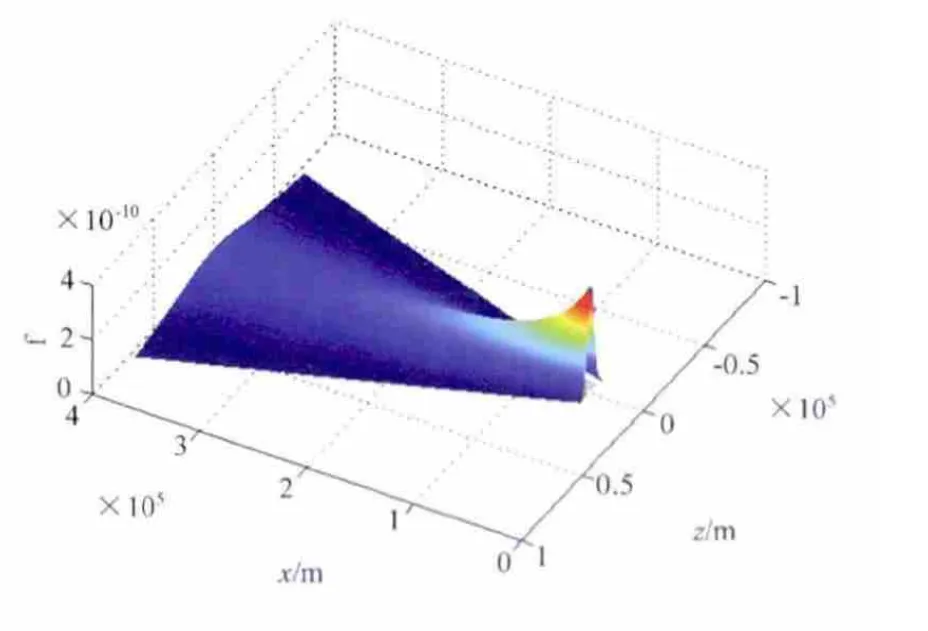
图8 单次测量目标概率分布

设载机对目标方位进行3次探测，将坐标系原点取在第二次探测位置，载机沿x轴正向水平飞行。假设目标位于距原点r＝100km，φ＝90°处，探测间隔距离为L＝10km。概率法仿真结果如图9所示。

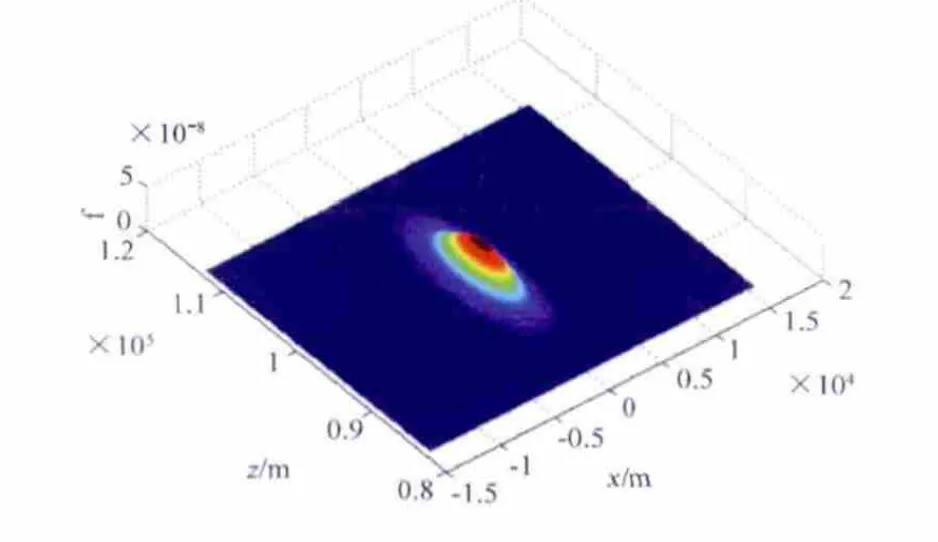
图9 目标联合离散概率密度分布

4.3 方位角速率法

不同情况下目标估计距离r与方位角示值变化率仿真及对比效果如图10所示。

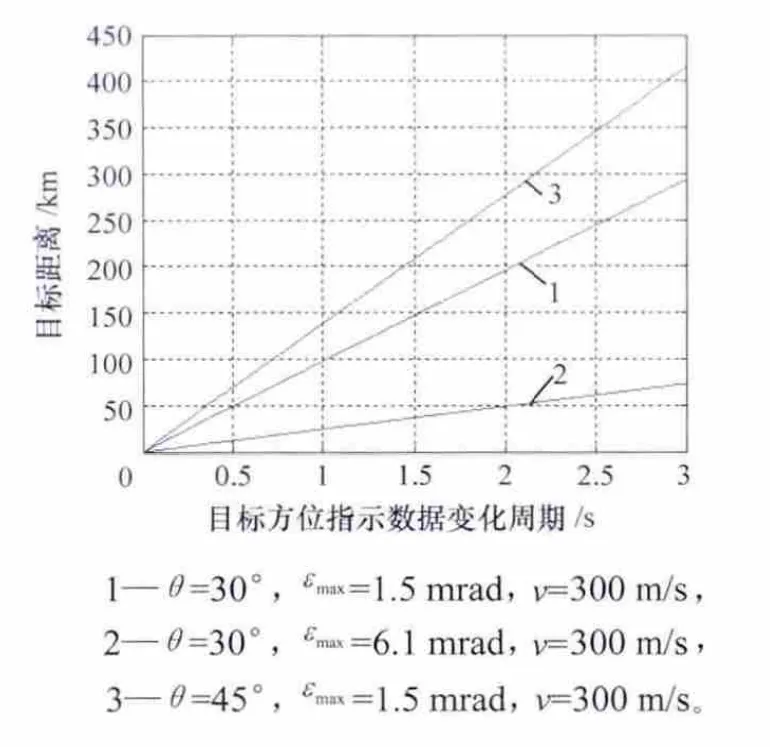
图10 方位指示数据变化周期与目标距离的关系

令vP＝300m／s，＝10－10rad2／s2（平均角速度方差），εmax＝π／512，＝4×10－4rad2，＝10 m2／s2，＝3.765×10－9。可计算距离估计方差随θn＋1，rn＋1变化情况，仿真结果如图11所示。

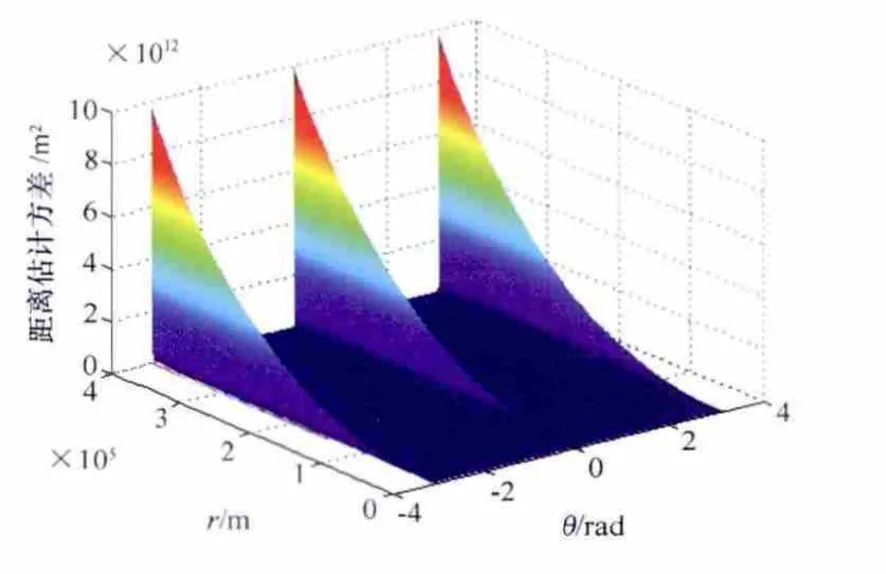
图11 距离估计方差（无源雷达）

4.4 目标捕获

导弹自控终点误差3.5km，搜索扇面张角80°，搜索距离20km，采用2枚导弹对目标区进行搜索攻击，仿真效果如图12所示。

图12 目标区搜索仿真结果

5 结束语

综合仿真实验系统提供了各种处理方法的标准仿真模型，统一了仿真实验环境和结果表示形式，使得各种方法的处理效果具有可比性。实验用户不必将主要精力放在仿真环境构建、模型验证、仿真程序编制等方面，而是通过不同条件下的仿真参数设置获得直观的仿真结果并进行对比分析，从而获得更好的教学效果。

（

）

［1］田锦昌，袁健全，孔玉，等.空舰导弹制导雷达适应复杂电磁环境方法分析［J］.航天电子对抗，2010，26（6）：12－13.

［2］芮国胜，康健.机载被动定位系统仿真研究［J］.计算机仿真，2003，20（9）：27－28.

［3］杨建华，陈思兴.国外机载快速无源定位技术最新发展［C］／／雷达跟踪技术研讨会论文集.2001：38－40.

［4］凌霖，苏胤杰，晋春.软件仿真在通信原理实验教学中的应用［J］.实验技术与管理，2011，28（4）：83－85.

［5］刘伯红，阎英，方义秋.高校计算机实践教学质量保障体系改革探索与实践［J］.实验室研究与探索，2012，31（12）：121－123.

［6］朱昌平，施铃泉，王斌，等.讲授好“卓越计划”高频电路理论与实践课程的探索［J］.实验技术与管理，2012，29（10）：142－145.

［7］冯毅平，张光新，荣冈.基于知识系统化重构的研究型实验教学［J］.实验技术与管理，2012，29（10）：154－156.

［8］徐凯，徐果微.基于“实验比较法”的电气信息类研究生培养教学探究［J］.实验室研究与探索，2012，31（9）：135－138.

［9］张晔.基础实验中科研能力的培养［J］.实验室研究与探索，2012，31（12）：91－92.

［10］Taek L Song，Tae Yoon Um.Practical guidance for homing missiles with Bearing－Only measurements［J］.IEEE Transactions OD Aerospace and E1ectronic Systems.1996，32（1）：434－443.

［11］Hammel S E，Aidala V J.Observability requirements for three－dimensional tracking via angle measurements［J］.IEEE Transactions on Aerospace and Electronic Systems.1985，21（2）：200－207.

［12］孙涛，谢晓方，梁捷，等.纯方位目指条件下空舰导弹目标搜索策略研究［J］.弹箭与制导学报，2011，31（5）：72－74.