靶场光电经纬仪交会测量数据处理方法比较分析＊

刘 亮 李海燕 胡云安 何友金 杨建强 侯建军 娄树理

（1.海军航空工程学院控制工程系 烟台 264001）（2.中国人民解放军驻三三〇三厂军事代表室 武汉 430200）

1 引言

光电经纬仪因具有测量精度高、直观性强、抗干扰能力强等优点，常用于对空中及地面目标的无源探测、跟踪和定位［1］。由于只能得到目标相对观测站的方位角和俯仰角，单台光电经纬仪不能确定目标的空间位置。加装激光测距机后，虽然单台经纬仪可以实现定位，但其测量精度比交会测量低。因此，靶场测量中通常采用两台（或多台）光电经纬仪的测量数据经过交会计算获得目标的空间坐标［2～3］，进而可以得到目标的运动参数和空间姿态［4］。

两台（或多台）光电经纬仪交会测量时，常用的外弹道计算方法有L公式法［5］（水平投影法）、M 公式法［6］（垂直投影法）和异面直线法［7～9］。前人对上述计算方法进行了大量的研究工作，例如：文献［5］基于L公式法，分析了两台经纬仪交会测量误差，并提出了四台经纬仪两两交会测量结果的加权融合处理方法，该方法利用了C24组测量信息，融合处理得到的测量误差小于任两台经纬仪的交会误差。文献［7］基于异面直线法研究了组网测量中交会角、方位角、俯仰角和基线长度对定位准确度的影响。文献［6］对上述三种计算方法的适用范围进行了分析。目前，没有文献对文献［5］中的融合处理方法和异面直线法进行比较分析。

本文在文献［5］基础上，提出了改进后的加权融合处理方法，解决了文献［5］中的方法不能适用于两站交会测量的问题，在此基础上对两台及三台经纬仪的交会测量进行了仿真分析，并将改进后的算法于与异面直线法进行了比较分析。

2 多台经纬仪交会测量原理

2.1 L公式法

图1 L公式法示意图

假设发射坐标系为OXYZ，测站及待测目标的空间如图1所示。O1（x1，y1，z1）、O2（x2，y2，z2）、为经纬仪站点位置，M（xm，ym，zm）为待测目标的空间位置。两台经纬仪测得的目标的方位角和俯仰角分别为αi和λi，（i＝1，2）。

两台经纬仪进行交会测量，假设两台光电经纬仪观测同一目标时其主光轴并相交于目标上同一点，根据立体几何知识，可得M（xm，ym，zm）的坐标可用下式表示

可以看出，式（1）中不包含第二个经纬仪的俯仰角2，即两台经纬仪进行交会测量时，以第一台为主，第二台为辅。因此，类似可得：

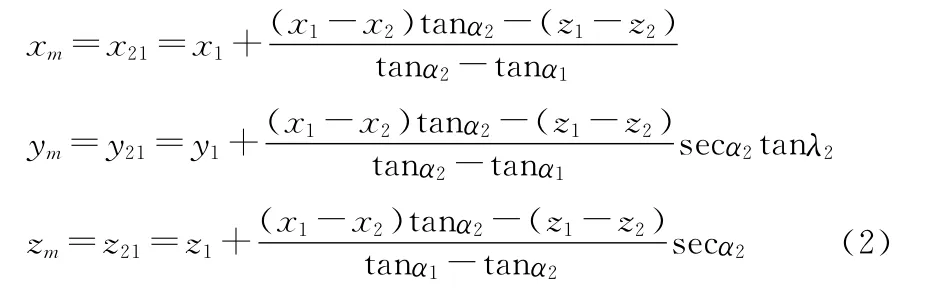
由式（1）～（2）可知，目标位置为站点位置、方位角和俯仰角的函数，由误差传递定律可知，误差来源于两部分：一部分是光电经纬仪测角误差；另一部分是大地测量坐标值的误差。前者不可避免地会给目标位置测量带来误差，后者可通过高精度的大地测量使其足够小，以致给空间坐标测量带来的误差完全可以忽略不计。在本文的分析中，假设由大地测量所导致的误差可以忽略不计，同时为了分析的方便，假设两台经纬仪在方位角和俯仰角方向的测量误差均相等，即σα1＝σλ1＝σα2＝σλ2＝σ0，则根据误差传递定律可知L公式法的测量误差为

其中，

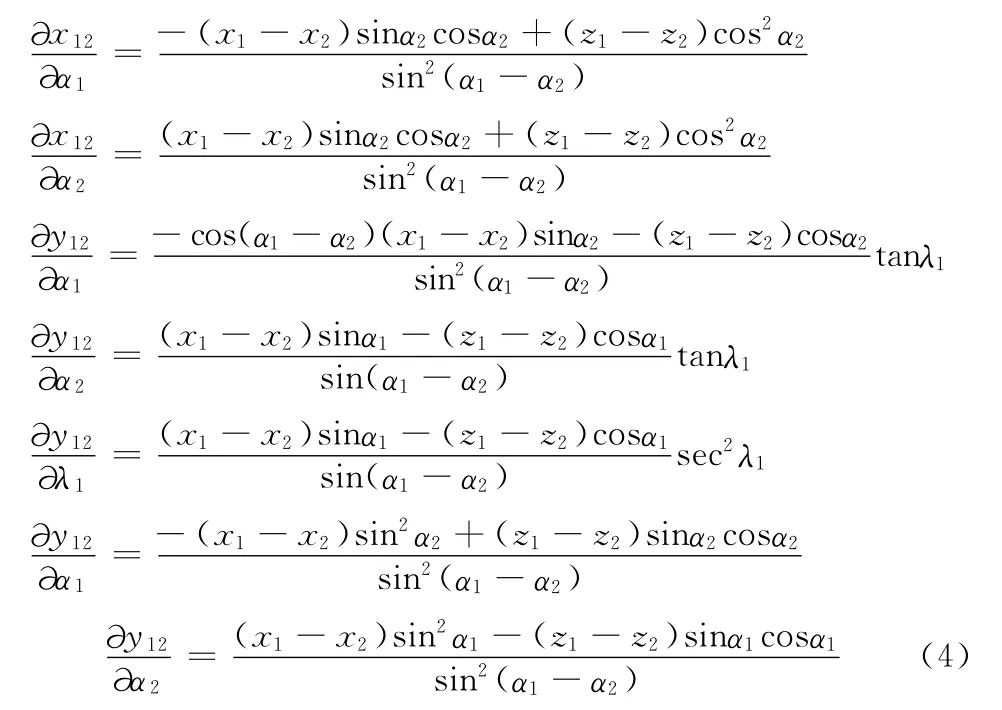
如果利用n台经纬仪进行两两交会测量，则第i，j台经纬仪交会测量后所得的目标空间坐标（xij，yij，zij）由式（1）给出，只需将式（1）中的下标1，2分别换成i，j（i≠j）即可，这样共得P2n组交会测量结果。将这P2n组交会测量结果进行如下数据融合最终所得目标的空间坐标为

融合后目标空间坐标均方差分别为

式中

上述方法与文［5］的差别在于式（7）不要求i＜j，即改进后的融合处理算法可利用的测量结果组数（P2n组）多于文［5］的测量结果组数（C2n组），且可对两台经纬仪交会测量进行融合处理。

2.2 异面直线法

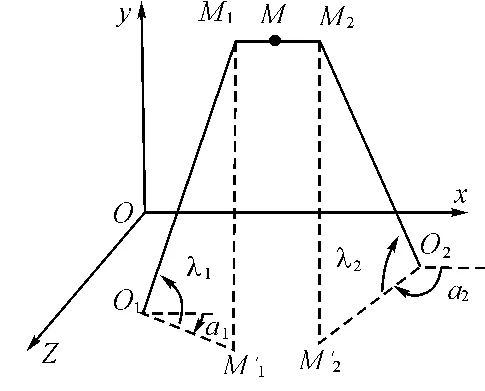
图2 异面直线法示意图

实际测量中，当目标具有较大的外形尺寸，跟踪测量时两台经纬仪跟踪测量的点通常不是目标上的同一点。此外，受经纬仪结构、成像原理、测角准确度、时间同步误差以及外界环境（所处地理位置、与太阳的夹角和大气折射等）因素的影响，两台光电经纬仪观测同一目标时其主光轴O1M1、O2M2并不相交于目标上同一点，而是呈现异面关系［10］，如图2所示。

假设目标点M与M1、M2点具有关系：M1M／M1M2＝ρ，ρ∈［0，1］，其中M1M2分别表示异面直线O1M1、O2M2的公垂线线段M1M2的长度，M1M表示线段M1M的长度，ρ为根据各经纬仪不同的测角精度适当选取的加权系数，则M点的坐标可以表示为

对于异面直线法的测量误差可按以下公式进行计算

式中∂xm／∂αi、∂xm／∂λi、∂ym／∂αi、∂ym／∂αi、∂zm／∂λi、∂zm／∂λi的形式较为复杂，这里不再累述。

3 仿真分析

3.1 两台光电经纬仪交会测量结果及其误差分析

设两台经纬仪之间的距离为Lm，其坐标分别为O1（-L／2，0，0）、O2（L／2，0，0），飞机在航高y为Hm，-2L≤x≤2L，-2L≤z≤2L的平面内飞行。光电经纬仪的方位角和俯仰角精度均为25″，测角误差符合正态分布。

本文的仿真流程为：首先设定经纬仪站点及目标飞行航迹，然后逆运算得出目标相对经纬仪的真实方位角和俯仰角，再以正态分布仿真实际误差分布，并按照相应的算法进行交会计算，得到被测目标的空间位置及其误差。

为了便于比较不同计算方法对测量结果的影响，以精度几何因子GDOP作为标准［11］，其定义为

它描述定位精度的三维几何分布情况，GDOP 因子越大，定位精度越低。在本文的仿真分析中，均假设实验测量精度要求为2m，并定义GDOP＜2m 的有效测量区域面积与面积4L2之比为Re。

图3 双站测量GDOP2 等值线分布图

图3及表1显示了L＝104，H＝103时，分别以（a）O1站为主O2站为辅；（b）以O2站为主O1站为辅；（c）综合利用O1、O2两站测量数据进行数据融合；（d）采用异面直线法获得的0～4m2之间的测量结果［GDOP］2等值线分布图，图中虚线为基线。计算结果表明：

1）以L公式法进行分析时，若采用以一个站的测量数据为主、另一个站的测量数据为辅的计算方法会导致基线方向测量误差分布的不均匀，其中主站一侧附近区域测量误差较大，而综合利用两站测量数据进行数据融合，或采用异面直线法进行分析可有效提高测量误差分布的对称性，提高主站附近区域的测量精度。其原因如下：在一站为主一站为辅的方式中，俯仰角误差λ1（或λ2）对两个测站附近区域的影响不同，而综合利用两站测量数据进行数据融合，或采用异面直线法进行分析时，由于站点1、2之间具有互异性，因此误差分布具有对称性。

2）综合利用两站测量数据进行数据融合，或采用异面直线法进行分析可扩大有效测量区域的面积。以一站为主一站为辅的方式测量时，有效区面积仅占测量区域面积的23.01%，综合利用两站测量结果，该比例提升至35.24%，采用异面直线法时该比例提升至37.33%。其原因如下：由式（7）～（8）及不等式知识可知，综合利用两站的测量结果得到的测量误差比任意一种主辅站搭配的测量误差都小，因此，使用L公式时，综合利用两站的测量结果比使用一站为主一站为辅的方式精度高，有效区域大。由式（3）可知异面直线法的失效条件为K→0，即α1→α2，且λ1→λ2。由式（1）可知L公式法的失效条件为tanα1→tanα2，即α1→α2或α1→π＋α2。可见，异面直线法的失效条件更为严格，因此其适用面积更大，包括了基线附近区域。

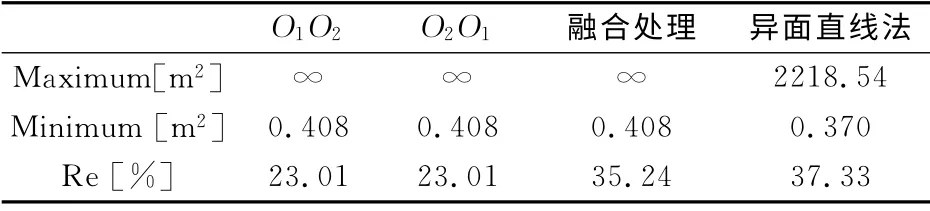
表1 双站测量GDOP2 的最大＼小值及Re值

3）采用双站测量时，目标沿基线的中垂线飞行时可获得最大保精度飞行航程，此时宜采用异面直线法。原因如下：改进的融合算法是基于L公式法提出的，测量有效区域不包括基线附近区域（如图4），在目标抵达基线附近时将存在较大测量误差，有可能造成丢失目标的情况；而异面直线法的测量有效区域包括基线附近区域，可以在全程满足测量精度要求。

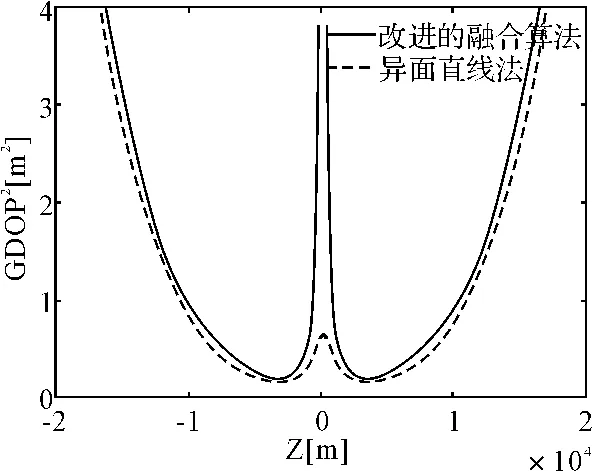
图4 z轴上GDOP2 分布曲线（x＝0）

3.2 三台光电经纬仪交会测量结果及其误差分析

图5显示相同测量条件下，y＝0平面上三个观测站以边长为L＝104m 的等边三角形排列时，分别采用异面直线法和改进后的融合处理法计算得到的误差分布。从仿真结果可以看出：与两站交会测量相比，三站测量可以大大提高测量的精度及有效测量区域的面积。同时，三站测量时即使采用基于L 公式的改进的融合处理方法，基线附近区域也可满足测量精度要求。

图5 三站测量时GDOP2 等值线分布图

图6分别显示了L1＝10km 和L2＝5km 时，GDOP2及有效测量区域面积占4L21的百分比Re随着目标飞行高度H的变化曲线，从仿真结果中可以看出：

图6 三站测量时GDOP2 及Re随H 变化曲线

1）随着目标飞行高度的增加，目标定位精度逐步降低，其中，异面直线法的定位精度下降趋势比改进的融合算法慢。原因如下：随着高度的增加，目标距离测量站的距离增加，从而相同测角误差导致的定位误差增大，因此定位精度随H增大而降低。由于测量误差的存在，实际测量中两台光电经纬仪观测同一目标时其主光轴并不相交于目标上同一点，因此异面直线法更符合真实的物理情况，因此测量精度比改进的融合算法高。

2）基线较短时，目标飞行高度对GDOP2的影响较大。原因如下：由式（5）可知，随着H的增加，俯仰角迅速增大，σy迅速增大，基线较短时，俯仰角增大的趋势更快。因此，长基线测量更适合爬升段的目标测量。

3）对于相同高度的飞行目标，基线较长时，有效测量区域面积较大。原因如下：相同高度条件下，基线越短，经纬仪视轴的俯仰角越大，测量误差越大。

4）当采用改进的融合算法解算目标弹道时，Re随着目标飞行高度的增加而减小；当采用异面直线法解算目标弹道时，Re随着目标飞行高度的增加，先增加再减小，且减小的趋势较平缓。

4 结语

光电经纬仪的测量精度不仅受制于仪器本身的精度，测量算法的精确性和测试方法的完备性也在很大程度上影响到测量结果的准确性。本文通过对两台经纬仪交会测量的研究发现：基于L公式法的双站测量系统，由于未充分利用测量数据，测量误差不关于基线的中垂线对称性；在文献［5］基础上，提出了改进后的加权融合处理方法，解决了文献［5］中的方法不能适用于两站交会测量的问题，对两台经纬仪的交会测量仿真分析表明：该算法充分利用冗余信息，不仅解决了误差分布不对称的问题，还可以大大提高测量精度和有效测量区域的面积。采用改进后的融合处理算法和异面直线法，研究了目标飞行高度和基线对三台经纬仪交会测量的影响，结果表明：长基线测量可获得更高的测量精度，并覆盖更大的测量区域；在一定飞行高度条件下，改进后的融合处理算法可获得与异面直线法相当的计算精度和有效测量区域面积，但随着目标飞行高度的增加，基于L公式的融合处理方法性能迅速下降。

［1］刘利生.外测数据事后处理［M］.北京：国防工业出版社，2000，254-260.

［2］石彦召，朱新华，郑百源，等.基于光电经纬仪的布站研究［J］.探测与控制学报，2009，31（Z1）：86-89.

［3］周杰，刘哲，刘长安，等.多台光电经纬仪布站几何的仿真研究［J］.计算机仿真，2011，28（8）：24-28.

［4］赵立荣，柳玉晗，朱玮，等.光电经纬仪单站空间余弦及多站面面交汇的飞机姿态测量［J］.光学精密工程，2009，17（11）：2786-2793.

［5］张玲霞，马彩文，陈明等.靶场光电经纬仪多台交会测量数据的一种处理方法［J］.测绘学报.2003，32（2）：139-142.

［6］傅晓程，王小海.光测设备数据交汇计算方法研究，浙江大学学报，2008，35（2）：173-177.

［7］侯宏录，周德云.光电经纬仪异面交会测量及组网布站优化设计，光子学报，2008，37（5）：1023-1028.

［8］侯宏录，李宏.光电经纬仪测量飞行器三维坐标方法和误差分析［J］.光电工程，2002，29（3）：428.

［9］吴能伟，陈涛.光电经纬仪目标异面交会测量的误差分析，［J］中国仪器仪表，2006，（6）：49-51.

［10］赵学颜，李迎春.靶场光学测量［M］.北京：国防工业出版社，2001.

［11］崔书华，胡绍林，李果.光电经纬仪布站分析及优化［J］.光学与光电技术，2007，5（5）：12215.