基于径向基神经网络的舰艇磁场推算模型＊

（91388部队 湛江 524022）

1 引言

近年来，闭环消磁技术成为各国消磁研究热点，相较于目前的消磁系统控制方法，它可以实现固定磁场的实时补偿，是未来磁隐身技术发展的必然趋势。为了获取较多的舰船内部信息，以及实际中舰船内部传感器的安装问题，传感器应该与船壳非常接近，测量所得的磁场是舰艇内部复杂的近场值。相对于目前较成熟的磁场深度推算问题，内外磁场推算属于不同的半空间，且存在磁屏蔽现象，很多深度换算中的成功模型（如：磁偶极子等）难以直接应用［1］。因此，寻找一种根据舰船内部磁场测量值有效推算舰船外部某特定深度上磁场的方法成为实现闭环消磁技术的关键，也是闭环消磁技术亟待解决的问题之一。

国外对舰艇内外换算方法较早进行了研究，文献［1］利用积分方程法，建立了基于薄壳体内外换算的一种有效模型，但它只解决了船壳内外感应磁场换算的问题，对于固定磁场以及增加设备后的舰船内外磁场没有进行深入研究。文献［2］提出了一种利用虚拟磁源法（Virtual source）建立舰船磁场内外换算的数学模型，但只进行了原理说明，没有具体的实验验证其换算精度。文献［3］在文献［2］的基础上，进行了理论上的改进，其主要原理是利用当前磁化状态下的舰船内部磁场与内部校准矢量（Onboard Calibration Vector）计算得到比例系数（Scale Factor），将所得的比例系数与外部校准矢量（Offboard Calibration Vector）相乘，就可得到当前舰船外部磁场值。文献［4］从磁势的角度出发，建立了双层壳潜艇的感应磁场直接计算模型，并反演出固定磁场值，其换算精度较高，但其要求铁磁材料的一些重要参数为已知，而这些参数在实际中一般很难得到。国内对闭环消磁技术的研究尚处于起步阶段，文献［5］在文献［3］的基础上，通过船模实验验证了基于变化量的校准矢量进行磁场推算的有效性。文献［6］从位置优化的角度出发，对薄钢板两侧磁场推算进行了研究，提高了薄钢板两侧磁场推算精度，但尚未涉及船模的内外磁场换算研究。上述文献大多是采用线性化方法解决内外换算问题，可能会面临网格剖分、复杂的重积分计算、反演过程中方程不适定以及对于数据具有选择性等问题，且随着舰船的大型化，铁磁设备多样化将会加剧线性建模的难度，影响其换算精度。本文从智能优化的角度出发，建立了内外磁场之间的RBF神经网络预报模型。该方法避免了利用数值建模技术存在的诸多困难，即可实现舰艇内外磁场的换算，相较于其他数值建模方法其换算精度有所提高，并利用船模实验验证了所得网络的有效性和良好的泛化能力。

2 舰船磁场内外推算的数值模型

文献［3］中提到的校准矢量法具有原理简单、换算方便（不必网格剖分，不涉及复杂重积分计算）等优点，本文选取校准矢量法作为数值建模的代表。该方法从虚拟磁源的理论出发，认为舰艇内外磁场均是由磁源产生的，如图1所示为内外磁场换算示意图。

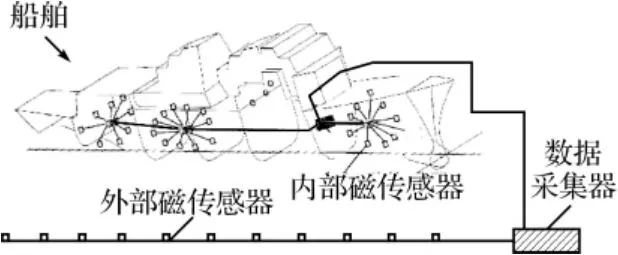
图1 舰船磁场内外换算示意图

当磁场大小发生改变时，代表磁源的大小或方向发生改变，而内外传感器的位置相对于磁源位置是相对固定的，用矩阵表示如方程（1）所示

其中，Mi代表磁源在第i种磁化状态下的磁矩列向量，Hi、H′i分别代表舰船内、外部磁场强度值组成的列向量，Aon、Aoff分别代表联系磁矩列向量与磁场强度的线性观测矩阵，矩阵中的每个元素由内外传感器布设位置与磁源布设位置决定。选取一部分磁化状态下的Hj与H′j（j＝1，…，m，1＜m＜f）分别作为内、外校准矢量，则某一磁化状态下，内、外磁场强度值Hk与H′k（k∉j）与内、外校准矢量Hj与H′j之间的比例关系为

其中SF、SF′分别代表内、外部比例系数矩阵，观察方程组（2）发现，对相同磁化状态下的一组内外磁场列向量而言SF＝SF′。则可以先通过Hk与Hj反演出SF，将其代入方程组（2），即可获得内、外磁场强度值Hk与H′k（k∉j）之间的换算关系为

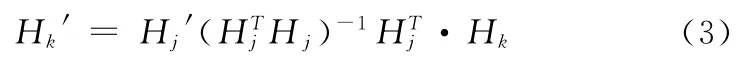
综上所述为目前国内外学者针对内外换算问题提出的较先进的线性建模方法，其误差主要来源于测量误差以及反演校准矢量SF时方程不适定造成的误差。与最常用的BP神经网络相比，RBF［7～10］神经网络在逼近能力、分类能力和学习速度方面均优于BP 网络，为此选择该网络作为智能优化的代表。

3 RBF神经网络模型基本原理

RBF神经网络是一种具有单隐层的三层前馈网络，它模拟了人脑中局部调整、相互覆盖接受域的神经网络结构，由输入层、具有径向基函数神经元的隐层和具有线性神经元的输出层构成，如图2所示为一个典型的RBF神经网络结构图。径向基层单元的作用函数常取高斯基函数，可表示为如下形式：

神经元radbas的输入为输入向量p与隐层权值w1之间的距离（dist函数）与隐层阈值b1的乘积；输出层神经元传递函数为purelin，输出层权值为w2，输出层阈值为b2。选择Matlab工具箱中的newrb（）函数设计网络，该函数包含输入样本、期望输出、训练精度Goal和散布常数spread几个关键变量。其中散布常数的选择尤为重要，如果散布常数选择不当，会造成网络设计中神经元数过多或过少，进而在函数逼近中造成过适性或不适性，一般情况下，散布常数的选取取决于输入向量之间的距离，要求是要介于最小距离与最大距离之间。

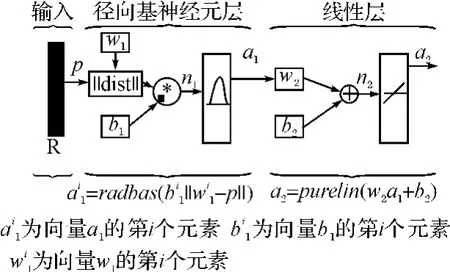
图2 径向基网络结构图

4 神经网络预报模型的有效性验证

4.1 基于RBF神经网络的潜艇磁场内外换算实验设计

选取一两端封闭的空心圆筒作为潜艇模型（长2002mm，厚6mm），选用一可以自由推入推出圆筒的测量架，以便布设内部磁传感器。将七个传感器等间距布设在测量架中心线位置，将其推入空心圆筒内部，用以测量潜艇模型内部磁场，并在模型正下方0.594m处，等间距布设七个传感器用以测量潜艇外部磁场，磁传感器具体布设如图3所示。

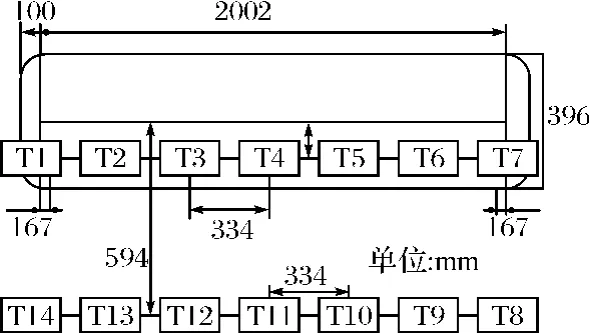
图3 传感器布设示意图

4.2 RBF网络基本参数的确定

通过改变敷设在船模外部导线中的电流来模拟模型固定磁化状态的变化。在得到12组不同磁化状态下模型的内外测量数据后，任意选取其中11组内外测量数据作为A组，剩余1组内外测量数据作为B组。则RBF神经网络的基本参数选取规则如下：

训练样本集：选取A组中的内部测量数据即文献［5］中的内部校准矢量Hj作为训练网络的学习样本，A组中的外部测量数据即文献［5］中的外部校准矢量Hj′作为训练网络的期望输出；

测试样本集：选取B组中的内部测量数据即文献［5］中的Hk作为测试网络训练效果的输入样本，B组中的外部测量数据Hk′即文献［5］中的作为网络的理想输出；

训练精度Goal：Goal＝0.00001；

散布常数spread：0.001。

4.3 网络训练以及网络评价

基本参数设置完毕后，输入学习样本训练网络，而后输入测试样本来测试网络的预测精度。为了方便与文献［5］中校准矢量法进行比较，本文选择与文献［5］中相同的最大相对均方根误差ERR 作为衡量预测精度的判定依据，其中ERR 定义为

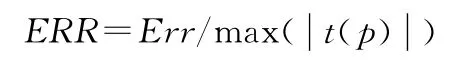
则12组利用校准矢量法的磁场推算误差［5］与本文提出的RBF神经网络预报误差比较图如图4所示，由图可见，RBF神经网络预测精度均优于校准矢量法磁场的推算精度，前者的ERR 最大值不超过3%，且大部分ERR 小于1%，而后者ERR 最大值大于6%，从而验证了基于RBF神经网络推算方法的有效性。且该方法的预报误差分布均匀，误差曲线较为平缓，说明RBF神经网络选用不同的基函数作为训练样本对预报结果影响较小。

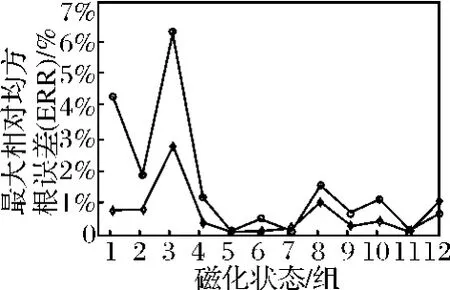
图4 两种方法建模时，ERR 比较图

5 结语

本文先从数值建模角度研究了舰船内外磁场之间的关系，利用数值建模技术会存在反演模型不适定的问题，且对于同一组数据而言，选择不同的校准矢量对换算结果影响较大。鉴于此，本文从智能优化的角度出发，建立了内外磁场之间的RBF神经网络预报模型，并通过船模实验验证了网络预测的准确性，相较于线性方法，换算精度有所提高，且有较高的稳定性，符合工程实际需求。

［1］Oliver C，Jeanlouis C，Jeant B，et al.Recent improvements for solving inverse magneto static problem applied to thin shells［J］.IEEE Transactions and Magnetics，2002，38（2）：1005-1008.

［2］Carl S.Closed-loop multi-sensor control system and method［P］.US PATENT 5189590Feb.23，1993.

［3］Richard M，Robert A.Ship degaussing system and algorithm［P］.US PATENT 6965505B1Nov.15，2005.

［4］Vuillerunet Y，Closed loop degaussing applied to double hull submarine magnetization identification from near magnetic fields measurements［D］.Grenoble，2008：25-30.

［5］王鲸，刘胜道，苏广东.一种潜艇内外磁场换算算法的实验验证［J］.海军工程大学学报，2010，22（1）：83-86.

［6］Wang Jing，Liu Shengdao，Su Guangdong.The Experimental Validation of Submarine’s Inside Magnetic Field Extrapolation from outside Magnetic Field［J］.Journal of Naval University of Engerneering，2010，22（1）：83-86.

［7］连丽婷，肖昌汉，刘胜道等.基于微粒群算法的薄钢板两侧磁场推算中的位置优化［J］.上海交通大学学报，2010，44（7）：0975-0979.

［8］董长虹.Matlab神经网络与应用［M］.北京：国防工业出版社，2007：64-110.

［9］Dong Changhong.Matlab Neural Networks and Applications［M］.Beijing：National Defense Industry Press，2007：64-110.

［10］张利平，孙美凤，王铁生.新型的RBF神经网络在水轮发电机组故障中的应用［J］.水力发电学报，2009，28（6）：219-224.

［11］耿志强，朱群雄，顾祥柏，等.基于多群竞争PSO-RBFNN 的乙烯裂解深度智能优化控制［J］.化工学报，2010，61（8）：1942-1948.

［12］夏红霞，王惠营，胡磊.基于粗糙集的神经网络结构优化方法［J］.计算机与数字工程，2010，38（5）.

［13］韩红桂，乔俊飞，薄迎春.基于信息强度的RBF神经网络结构设计研究［J］.自动化学报，2010，22（1）：83-86.