水平线列阵的最佳工作深度选择＊

（91388部队 湛江 524022）

1 引言

简正波模型采用简正波模式表示Helmholtz方程的解。Perkeris最早将该方法引入到水声学中，并详细地研究了Perkeris波导的声传播问题。随着数值计算技术的迅速发展，现在可以对任意边界条件和多分层边界条件进行求解。因此，简正波模型在水声学中的应用越来越广泛。

传统的声纳都要依托舰艇平台，因而受到许多限制，拖曳变深声纳的出现，部分地突破了上述局限。为扩展阵列声纳孔径，变深声纳的拖体逐渐演变成数百米的长线阵列，形成了拖曳线阵列声纳。研究线列阵的最佳工作深度对于拖曳线列阵声纳的作战使用具有重要的意义。

2 简正波声场模型原理［1～3］

为了获得波动方程的精确积分解，通常假定海洋为柱面对称的分层介质。由位于二维平面内rs＝（0 ，zs）的单频点声源激励，在r＝（r，z）处产生的声场满足柱坐标下的Helmholtz方程：

其中，ω为声源角频率，z取向下为正方向，c（z）和ρ（z）分别是与深度有关的声速和密度。应用分离变量法得到无激励的Helmholtz方程解的表达形式为pr，（ ）z＝φ（r）ψ（z）。将该表达式代入上式，并以表示分离常量，得到以下两个方程：

其中，式（2）是深度方程，即简正波方程，它描述了波动方程解的驻波部分；式（3）是距离方程，它描述了波动方程解的行波部分。于是，每个简正波，从水平方向看是一个行波，从深度方向看是一个驻波。

简正波方程（2）形成了本征值问题，它的解是Green函数。距离方程（3）是零阶Bessel方程，它的解可写成零阶Hankel函数。简正波理论将声压场表示成简正波张开或叠加的形势，并通过满足一定边界条件的简正波方程和距离方程分别来获取其本征值和本征函数［8～9］。在柱坐标系下，由Helmholtz方程（1）得到声压的简正波解表达式：

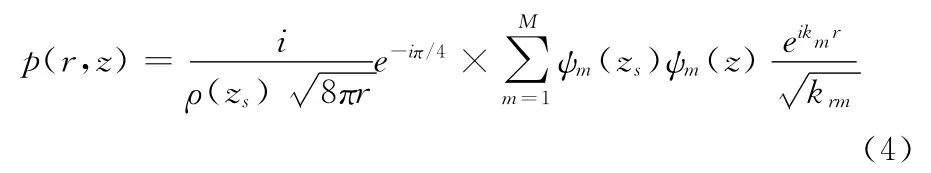
其中，ρ（zs）为声源处的介质密度，krm和ψm（z）分别为简正波的第m阶模态的本征值和本征函数。M为波导中有效传播的简正波模态书。

分局求解过程，可以知道波动中传播的简正波模态满足完备性和正交性，即：

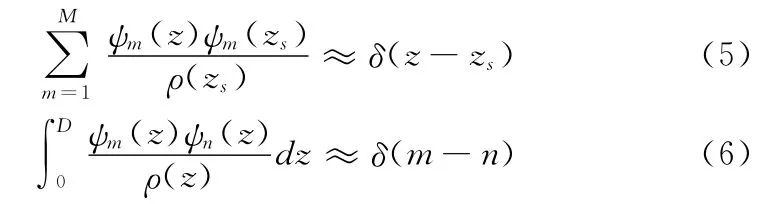
其中，D表示波导深度。开率深度离散采样的情况，采样点数为N，各个采样点的深度为zj，采样间隔为Δzj。当采样的深度跨越整个波导，且Δzj较小时，式（6）可以近似得到满足：

对于一定频率的声信号，仅有优先阶次的简正波可以在信道中有效传播。信号频率越高在信道中可以传播的简正波的阶次也越高；频率越低，可在信道中传播的简正波就越少，相应的模型计算量也会减少。因此，简正波模型在求解低频远距离声场时，具有精度高、运算量小的优点。事实上，在利用简正波模型求解声场时，频率也不能无限低。对于海底海面都是压力释放界面的波导，第m阶模态的截止频率为

对于给定的海洋环境，利用简正波模型可以非常高效、精确地计算出模态函数和相应的水平波数。这样，给定模式函数在声源和接收器深度的幅度及相应的水平波数，则任意位置的声源在接收基阵处的声压场就可以很容易计算得到。

3 水平线列阵的深度选择

水平线列阵（HLA）是水声信号接收、探测的常见阵列类型，在目标探测、方位估计等方面有着大量的实际应用，如图1就是典型的HLA 实际布放情况。浅海中，水声信号的传播受到声速剖面、海底海面反射等因素的影响，所以HLA 进行阵列信号处理时，其处理结果是与信道息息相关的。另一方面，通常情况下，对HLA 进行阵列信号处理计算时，为了简化计算，都假设HLZ 接收到的信号为平面声波［6］。然而，海上应用时接收到的声波信号多数情况都并非平面声波的情况，阵列信号处理结果必定受到影响。因此，通过HLA 在不同深度下的阵信号处理的计算，可以得到HLA 的最佳工作条件，从而提高其实际应用的效果。

目前国内外关于声纳工作深度的选择上，对主动声纳讨论较多，拖曳阵由于阵列孔径大，在水下工作更容易受到信道的影响，已经不能简单地用工程经验公式来计算。

考虑一个仿真环境，假设有一条阵元个数为64、间距为1.5m 的HLA，在图2所示浅海环境下如图1所示布放，我们利用简正波理论模型计算HLA 各个阵元接收到的信号。

为了计算不同深度时HLA 的工作性能，假定简正波模型计算网格为深度1～100m，垂直间隔1m，水平距离1～30km，水平间隔100m，即HLA 相对于声源的不同深度和距离。假定声源相对于HLA 中心的角度分别为45°、90°。选择阵列信号输出强度和目标估计方位做为衡量标准。

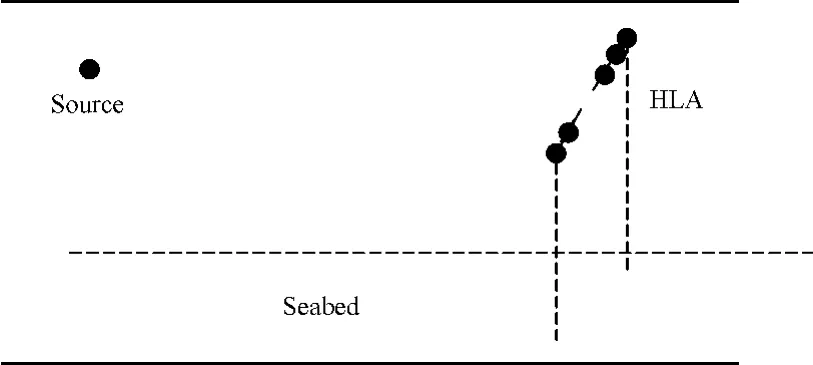
图1 典型HLA 布放情况示意图

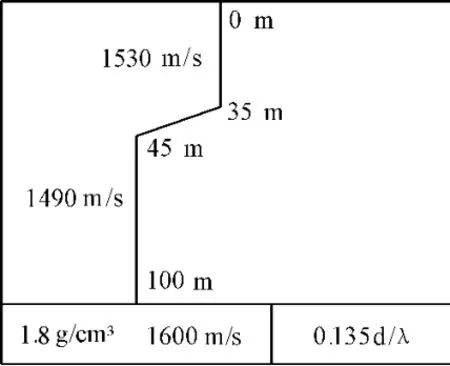
图2 典型夏季声速剖面

3.1 阵列输出信号强度

HLA 阵列信号输出时，我们选择了常规的均匀加权。对于计算得到各个相应深度、距离的阵列信号输出通过归一化的方法，并转化为分贝，来比较其差异。

由图3和图4可以看出，当水平阵和目标均位于负跃层同一侧时，水平阵的工作性能较好。

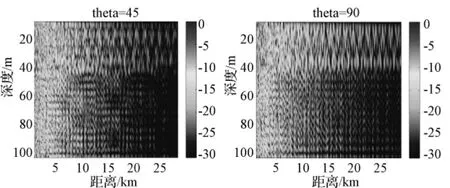
图3 声源深度30m 时HLA 阵列信号输出

3.2 目标方位估计（DOA）

在进行目标方位估计时，由于声波在信道的多途传播作用，使得目标信号到达方向往往会发生偏差。采用常规处理方法，结合简正波声传播模型，对目标方位进行估计，得到各个相应深度、距离上HLA 进行DOA 时角度误差。

可以看出，当目标位于阵的正横方向时（90°），估计出的方位误差很小。而当目标逐渐靠近阵的端射方向时，估计的方位误差增大。对于夏季声速剖面，当目标和线列阵位于负跃层同一侧时，方位误差较小，位于两侧时，误差增大。可见负跃层对于声信号在阵列上的响应影响很大。

图4 声源深度30m 时HLA 阵列信号输出

图5 声源深度30m 时DOA 方位角估计误差

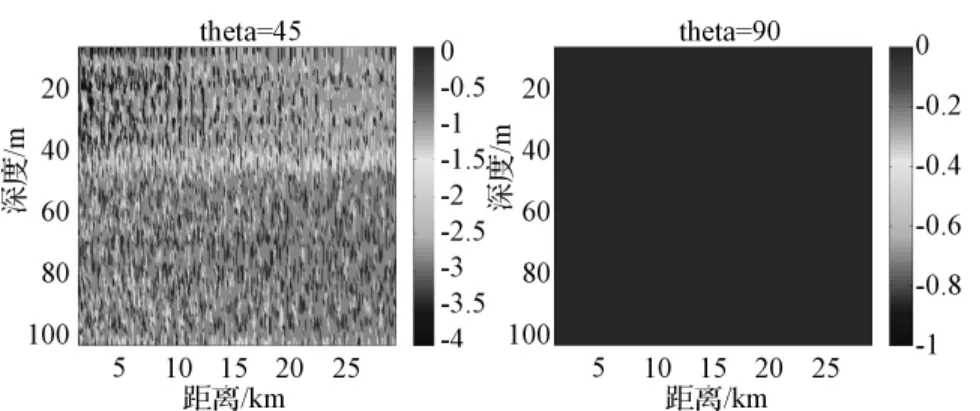
图6 声源深度70m 时DOA 方位角估计误差

因此，在对水平阵深度选择时，应考虑以下几点：

1）声速剖面对目标在阵列上响应的影响。声波在信道中传播时，在不同深度上，幅度响应、相位响应以及相关半径特性与声速剖面有着很大的关系，因此应该按照浅海声速剖面的不同，结合简正波声场模型，进行分类讨论，寻找影响阵列响应的物理因素。

2）不同深度上海洋噪声的空间分布与相关性。海洋噪声在不同的深度上有着不同的空间分布特性和相关性，这些噪声作用在拖曳阵上后，会对阵列输出信噪比产生明显的影响。因此，需要充分研究空间噪声的分布特性和相关性，降低在线列阵各个阵元的输出噪声相关性。

3）特定距离范围内阵列输出的统计特性。由前面的仿真结果可以看出，在不同距离上，由于声波传播的多途起伏效应，阵列的输出强度也是起伏的，实际接收信号由于具有一定的窄带带宽，需要研究窄带信号在阵列上的输出能量，按照阵列输出信噪比的某一统计特性作为阵列深度选择标准。

4 结语

通过以上分析，可知水平线列阵的工作深度与声速剖面、海洋噪声等都有密切的关系。仿真结果表明，阵列输出信噪比的某一统计特性可作为阵列深度选择标准，对水平线列阵的最佳工作深度进行预报和计算，这对于提高拖曳线列阵声纳的探测能力具有重要的意义。

［1］Paul C E.水声建模与仿真［M］.第三版.北京：电子工业出版社，2005：260-295.

［2］张歆，张小蓟，李斌.基于Kraken简正波模型的浅海声场分析［J］.西北工业大学学报，2000，18（3）：406-408.

［3］Michael B Porter.The KRAKEN Normal Mode Program［K］／／DRAFT.SACLANT Undersea Research Centre，2001：1-196.

［4］Porter M，Reiss E L.A numerical method for oceanic acoustic normal model［J］.Acoust.Soc.Amer（S0001-4966），1984，76（1）：244-252.

［5］杜金燕，孙超.典型浅海声场环境中的简正波估计［J］.声学技术，2009，（28）：719-724.

［6］刘孟庵，连立民.水声工程［M］.杭州：浙江科学技术出版社，2002：72-73.

［7］Urick R J著，洪申 译.水声原理［M］.哈尔滨：哈尔滨船舶工程学院出版社，1990：60-71.

［8］Paul C Etter.Underwater Acoustic Modeling［M］.London：Elsevier Applied Science，1991：83-118.

［9］Finn B Jensen，Michael B Porter.Computational Ocean Acoustics［M］.New York：AIP Press，1993.

［10］Schmidt H.Numerical modeling in ocean seismo-acoustics.Proc IEEE Oceans 91Conf，1991：84-92.