基于随机共振技术的微弱信号检测方法＊

（1.91388部队 湛江 524022）（2.南昌大学科技学院 南昌 330029）

1 引言

传统的微弱信号检测方法都是尽可能地抑制噪声来提取微弱信号，但是，在一些非线性现象中，噪声的存在却能够提高系统对有用信号的响应，会发生噪声能量向信号能量的转移，使得输出信噪比增强并达到极值点。这些现象中，随机共振［1～4］（SR）得到了广泛的研究，因此利用随机共振技术检测微弱信号不需要抑制噪声。这一理论为弱信号检测与处理提供了一条崭新的思路。

本文针对以海洋环境噪声为背景的水声微弱信号检测进行研究，探讨了随机共振技术在阵列信号处理一些算法中的适用性，并且给出处理方法，自适应调节系统参数，将阵列信号通过多路随机共振器后输出，从原理上保证了系统的可行性。再搭建采集系统，采用NI公司的LabVIEW 8.5图形化软件设计［5］，实现了微弱信号的采集与分析，为强海洋环境噪声下水声微弱信号采集与分析提供了一定的理论与应用基础。

2 随机共振的基本原理

随机共振（Stochastic Resonance，SR）理论最初是由意大利学者Benzi等提出，用来解释气象中每隔10万年左右冰期和暖气候期周期交替出现的现象。当时及随后一段时间并未引起人们广泛的关注，直到在一次双稳环激光器的关键实验中展示了随机共振现象，才迎来了随机共振的现代发展时期。随机共振系统一般包含三个不可缺少的因素：1）环境稳态系统；2）低于势垒的输入信号（如周期信号）；3）系统固有的或追加到相干输入中的噪声源。通常用于研究的随机共振系统都是由非线性朗之万（Langevin）方程描述的非线性双稳态系统所定义的：

方程（1）中s（t）＝Asin（Ωt＋φ）＋ζ（t）为该非线性双稳系统的输入信号，其中Asin（Ωt＋φ）为待测微弱周期信号，a、b是大于零的实数；A为信号幅值；Ω为调制频率；ζ（t）为噪声，且满足统计平均E［ζ（t）］＝0，E［ζ（t）ζ（t＋τ）］＝2Dδ（t-τ）。其中D为噪声强度，噪声方差为2D，τ为时间延迟。当A＝0，ζ（t）＝0时，系统、x＝0处的两个势阱点和一个势垒点分别对应势函数曲线中的两个极小值和一个极大值，此时质点位于两个势阱中的任意一个，视系统的初始状态而定。当A≠0时，整个系统的平衡被打破，势阱在信号的驱动下发生倾斜。在静态条件下，当A＜Ac（Ac为系统双稳态临界值）时，系统的输出状态将在处的势阱内作局部的周期运动，当A≥Ac时，系统的输出状态将能克服势垒在势阱间周期运动。然而，当系统噪声D≠0 时，在噪声的协同作用下，即使A＜Ac时系统也能在势阱间按信号的频率作周期运动。由于双稳态之间的电压差远远大于输入信号的幅值，使得输出信号幅值大于输入信号的幅值，同时因为系统输出状态的有规则变化，有效地抑制了系统输出状态中的噪声强度，因此系统的输出信噪比得到了提高，即输出信号得到了增强，这种现象从本质上讲是信号、噪声和非线性系统之间的协同作用，称之为随机共振。

3 随机共振模型与阵列信号处理中使用随机共振系统

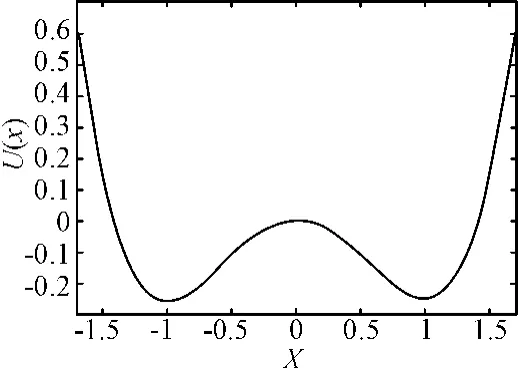
图1 双阱势能场，a＝b＝1

我们使用一种已经被深入研究的随机共振系统，基于下面的双稳态模型。设想一个质点在周期力和噪声作用下在双阱势能场中运动，如图1所示。模型可以用方程（1）［6］来 表 示：其 中，x（t）是输出信号，U（x）＝-ax2／2＋bx4／4是势能场，势垒高度为ΔU＝a2／4b，势能场最低点位于这里，我们假定噪声ξ（t）是零均值高斯白噪声，自相关函数为E［ξ（t）ξ（t＋τ）］＝2Dδ（t-τ）。

在信号不存在的情况下，质点在两个势阱间来回翻转，由噪声驱动的阱间翻转率由Kramers公式［7］给出：

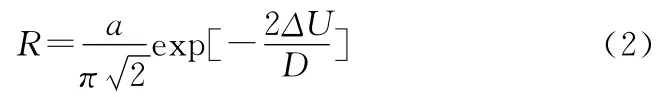
当引入一个微弱的周期力后，噪声驱动的阱间翻转可以与周期力同步。这种统计意义上的同步在噪声驱动的阱间翻转平均等待时间T（D）＝1／R满足时间匹配条件时发生［8］，即

这里TΩ是周期力的周期。由式（3）可以近似估计出噪声强度的最优值。

为方便，令初始相位φ＝0。在小输入信号幅度的情况下，系统响应可以表示为式（4）：

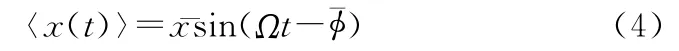
为幅度为相位。和的近似表达式为

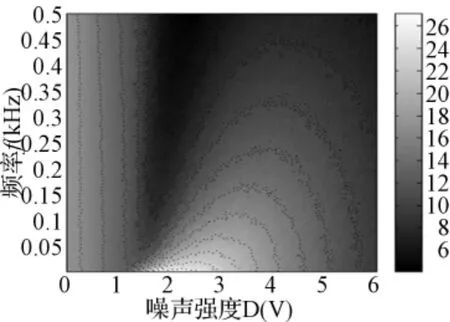
图2 输出SNR 随信号频率和噪声强度变化关系，a＝b＝1

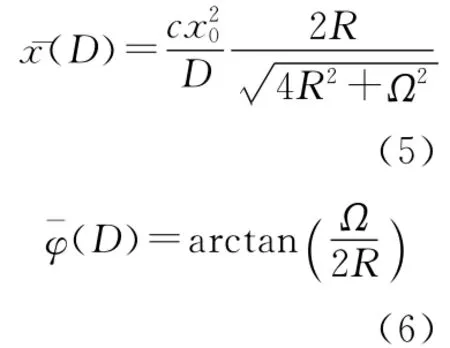
从以上分析中可以看出，有规律的信号的引入，导致了质点翻越势垒概率的有规律性。并且，通过时不变随机共振系统后，输出信号与输入信号之间保持了相位的一致性，但有一定延时（另可见文献［9～10］）。在阵列信号中，每路信号的延时是相等的。这保证了随机共振技术在阵列信号处理中的适用性。

随机共振系统对不同频率信号的响应是不同的。图2是我们通过实验得到的随机共振器输出信噪比SNR 随信号频率f和噪声强度D的变化关系。随着信号频率的增大，随机共振系统对微弱信号的“放大”作用逐渐减弱。因此，将随机共振技术引入阵列信号处理后，低频目标（或接收阵使用高采样率）将得到更有效的处理。

需要特别指出的是，随机共振技术对多种类型的信号和噪声均有效。我们仿真了单频信号、窄带信号，高斯白噪声、高斯色噪声等在不同信噪比的情况，均有很好的效果。

4 基于LabVIEW FPGA的数值仿真及分析

4.1 高斯白噪声数值仿真及分析

随机共振离不开高斯噪声的帮助，由于高斯分布是自然界中大多数随机事件所遵循的一种分布形式，因此噪声高斯分布的假设是与实际相当接近的。高斯白噪声一般用均值和方差来描述，假设噪声ζ（t）是均值为0，方差σ2＝2D的高斯白噪声，则有：

其中〈·〉算符代表总体平均，相应的噪声功率谱函数为

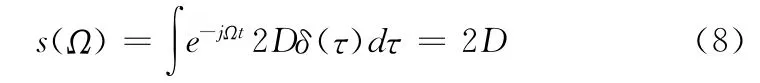
可见高斯噪声的功率谱是与频率无关的常量，称作白噪声。对于一般噪声ζ（t），要全面掌握其统计性质，还需要考虑其高阶矩，而对于高斯分布的函数而言，其高阶矩都可以表示为均值和方差的函数：

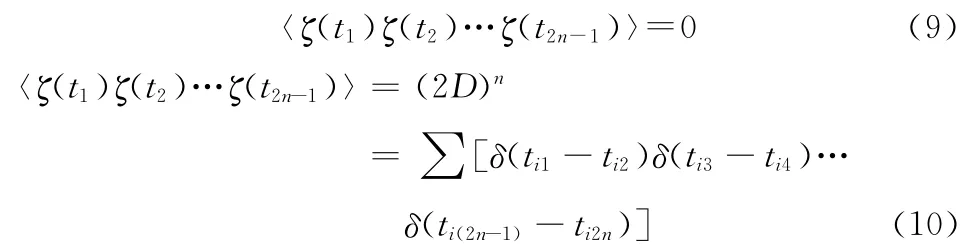
对于满足式（7）、（9）及（10）的噪声，即是具有高斯分布形式的白噪声，简称为高斯白噪声。在实际中，真正的白噪声是不存在的，因为它需要无穷大的功率才能产生出来。噪声总是有一定的相关时间，具有非零相关时间的噪声称为有色噪声。当有色噪声的相关时间远小于系统的时间常数时，仍可将色噪声当作白噪声进行处理。其时域图和功率谱图如图3和图4所示。

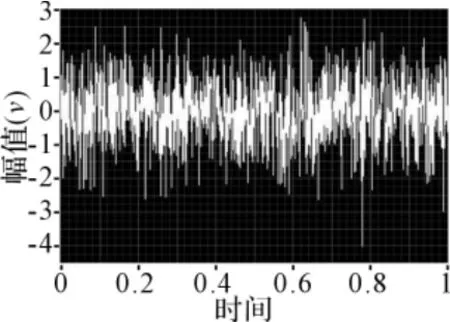
图3 高斯白噪声时域图

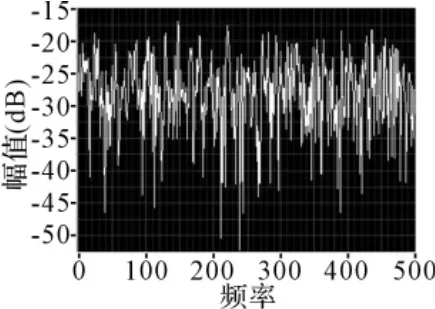
图4 高斯白噪声功率谱图

4.2 强高斯白噪声背景下的信号检测

海洋环境噪声是指声呐工作时的背景噪声。当利用声呐方程推算自导作用距离的时候，要求对背景噪声级NL做出估计。近年来，人们广泛采用海底深水水听器在低于1Hz～100kHz的频段范围内对深海噪声进行测量研究，大大扩展了人们对深海噪声源及其特性的认识，深海环境噪声是多种源的综合效应，包括潮汐和波浪的海水静压力效应、地震扰动、海洋湍流、远处行船、海面波浪和海洋分子热噪声等。海洋中的自然噪声源除了上述提到的之外，还有一类被称为间歇源，它们是一种暂时存在的噪声源。实际测量结果表明，与其他许多水声参量一样，海洋环境噪声有着明显的易变性，这是由于噪声源的易变性引起的。由于海洋环境噪声是由大量的噪声源辐射噪声所组成的，根据统计学的中心极限定理指出的：在非常宽的条件下，N个统计独立的随机变量之和的分布，在N→∞的极限情况下，趋于高斯分布可知，它的振幅分布应该是高斯型的。严格的来说，海洋环境噪声是各向异性的，在仿真过程中，对海洋环境噪声进行了简化处理，近似的将其看作是服从高斯分布的色噪声［11］。在仿真实验中，输入的混合信号是s（t）＝Asin（Ωt＋φ）＋ζ（t），其中ζ（t）是仿真的高斯海洋环境噪声信号。取参数A＝1，φ＝0，f＝100Hz，噪声强度为0.6，得到混合信号：s（t）＝Asin（200πt）＋ζ（t）。对淹没在强噪声中的微弱空间信号，用一般的阵列信号处理方法已经很难估计出其信号成分（如图5、图6所示）。如何提高在低信噪比情况下的处理能力，是阵列信号处理中一个很关键的问题。我们希望能用随机共振技术来解决上述问题。

图5 随机共振系统输入端信号时域波形图

图6 随机共振系统输入端信号频谱图

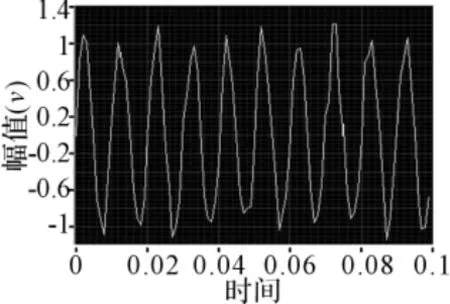
图7 随机共振器输出端信号时域波形图

图8 随机共振器输出端信号频谱图

我们在仿真和实验中采用了两种使系统进入随机共振状态的方法：一种是自适应的调节式（1）中的参数a，b，即事先得到对应不同信号和噪声特性时的最优参数a，b，在实际应用中根据情况选用；一种是自适应的调节外加噪声，在随机共振器中，可以加入适量噪声rn，使输出信噪比最大。可以采用自适应的方法来调节应加入的噪声rn。对于双稳态随机共振器，我们采用Euler-Maruyama方法［12～13］的离散形式来进行计算机仿真，实现式（1）。a＝1，b＝1时un是单个阵元接收到的被强噪声污染的目标信号，xn是经自适应随机共振器后的输出信号。初始条件为x0＝x（0）。其中wn为零均值高斯白噪声，方差为1。系数乘以wn使得满足维纳增量过程［10］。自适应学习过程的采样周期TS可以不同于仿真中的时间步长ΔT。对于双稳态系统，我们使用1∶20的降采样率。输出结果的SNR分析，及自适应调节算法参见文献［13］。

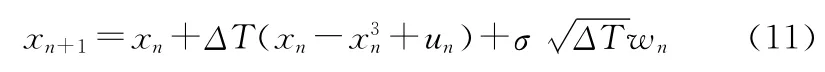
5 仿真结果分析

信号场和噪声场如果是时间平稳的，那么参数σ的学习过程可以先于信号估计完成。如果信号场噪声场时间不平稳，那么σ的估计值随时间缓慢变化。

图6是随机共振系统输入端信号频谱图。从图中可以看出，在强噪声背景下，输入端用常规的频谱分析，已无法分辨出信号的频率。图8是随机共振系统输出端信号频谱图，通过随机共振器后，系统输出信噪比大大提高，信号频率能够很方便的检测出来。

对比图5～8我们可以清楚地看到，输入信号、噪声和随机共振系统之间达到匹配了，发生噪声能量向信号能量的转移，使得输出信噪比增强。这时，通过随机共振模型检测出来的信号显得十分明显。在频率f＝100Hz处有明显的增强谱线。说明在此频率处有一个很强的周期成分存在，该频率正好等于输入信号频率，即在海洋环境噪声的背景下仍能检测到微弱信号。

6 结语

随机共振是80年代初发展起来的一个非线性科学分支，理论和实践都没有完全成熟。应用于阵列信号处理中，更是一种新的尝试。本文探讨了随机共振技术应用于阵列信号处理中的合理性，给出了处理方法，并且基于Lab-VIEW FPGA 构建了随机共振检测系统，进行了计算机仿真。在信噪比很低时，利用随机共振器处理之后的阵列信号，很容易估计出目标信号。本文中的方法能有效检测淹没在强噪声中的微弱信号，其优越性是明显的。但在实际工程中还有很多问题需要考虑。例如：1）在自适应随机共振算法中，如何自动产生最优参数；2）如何检测含有多个频率的微弱信号。随着对声纳系统要求的提高和研究的深入，这些问题亟待解决。

［1］Roberto B，Alfonso S，Angelo V.The mechanism of stochastic resonance［J］.J.Phys.A：Math.Gen，1981（14）：453-L457.

［2］R Benzi，G Parisi，A Stuem.A theory of stoclmstic resonance in climatic change［J］.SIAM Journal on applied mathematics，1983，43（3）：565-578.

［3］Kurt W，Frank M.Stochastic resonance and the benefits of noise［C］.from ice ages to crayfish and SQUIDs：Nature，1995（373）：33-36.

［4］J.M.G.Vilar，J.M.Rubi.Noise suppression by noise［J］.Physical Review Letters，2001，86（6）：950-953.

［5］尹静，贺良国，王洪波.基于LabVIEW 的三维静磁场计微弱信号检测系统［J］.仪表技术与传感器，2011，33（6）：93-95.

［6］杨祥龙，江波，吴为麟，等.小信号检测中的自适应随机共振技术［J］.自动化仪表，2004，25（1）：8-10.

［7］A.S.Asdi，A.H.Tewfik.Detection of weak signals using adaptive stochastic resonance［C］.IEEE：ICASSP，1995：1332-1335.

［8］H.Risken.The Fokker Planck Equation［M］.Berlin：Springer-Verlag，1984：232-235.

［9］L.Gammaitoni，P.Hanggi，P.Jung，et al.Stochastic resonance［J］.Reviews of Modern Physics，1998，Vol.70（1）：223-287.

［10］A.K.Chattah，C.B.Briozzo，O.Osenda，et al.Signal-to-noise ratio in stochastic resonance［J］.Modern Physics Letters B，1996，10（22）：1085-1094.

［11］周关林，李钢虎，成静.海洋环境噪声背景下水声信号检测的新方法［J］.声学与电子工程，2009，92（2）：21-27.

［12］T.C.Gard.Introduction to Stochastic Differential Equations［M］.New York：Marcel Dekker，1988：138-145.

［13］Sanya M，Bart K.Adaptive stochastic resonance［J］.Proceedings of the IEEE，1998，86（11）：2152-2183.