一种舰船非线性隔振装置的仿真及谱特性研究＊

（1.海军工程大学动力工程学院 武汉 430033）（2.船舶振动噪声重点实验室 武汉 430033）

1 引言

在现代高科技条件下的海战中，声隐身性能是潜艇和鱼雷等水下航行器的重要技战术性能指标，而其机械振动引起的水下辐射噪声严重影响了隐身性能［1］。

潜艇辐射噪声一般分为两类：一类是纯频噪声，其频谱为线谱；另一类是宽带噪声，其频谱为连续谱。潜艇辐射噪声谱通常是连续谱和线谱的组合。潜艇辐射噪声的频谱特征随着潜艇航速的变化而变化。在高速航行时，宽带噪声在辐射噪声信号中占主要成分，而低速时，特别是在潜艇隐蔽航行状态下，机械噪声是主要噪声源，线谱占主要成分。线谱是潜艇噪声谱级中最显著的特征，即使在潜艇低速航行时，产生最低的噪声辐射情况下也可探测到。因此线谱成了现代被动声呐在水声对抗中检测、跟踪和识别目标的主要特征信号，是潜艇声隐身性能的主要危害［2］。

控制潜艇动力机械振动最常用的方法是隔振，即在被隔振设备与基础之间插入弹性隔振元件，以减小两者之间的动态耦合和不良振动的传递。一般的文献都假定隔振器的力学特性是线性的。但线性隔振系统对线谱的隔离能力有限，线性隔振器隔离低频振动的效果，线性系统具有频率保持性，所以线性隔振系统不能改变传递至艇体的振动的频谱结构，即不能改变潜艇辐射噪声的频谱结构［3］。

针对线谱是潜艇声隐身性能的主要危害且难以消除这一情况，人们开始考虑非线性隔振系统，期望利用非线性隔振系统出现混沌时其响应的功率谱呈连续谱这一特征，将混沌理论应用到机械设备隔振装置，以减弱或消除特征线谱，提高潜艇的声隐身性［4］。

非线性系统响应的功率谱与线性系统的功率谱有很大不同，对于离散系统已有结论，Feigenbaum［5～6］认为周期运动的频谱是离散的线谱，发生倍周期分岔时，功率谱中将出现分频及其倍频，每经历倍周期分岔1次，每2条相邻谱线之间都要出现1条新的谱线。经过无限次分岔到达混沌状态时，离散的线谱演变为连续谱。M.Nauenberg和J.Rudnick［7］就一维映射证明连续两次新出现的线谱的平均强度之比为20.96，即新出现的线谱平均强度比上一次下降13.21dB。对于连续系统的功率谱特性分析较少，对于功率谱的特性形成原因很少分析和讨论。非线性隔振系统是时间连续系统，离散非线性系统的功率谱的变化规律在非线性连续系统中是否仍然成立？线谱平均强度会如何变化？

若线谱平均强度随分岔次数的增加而降低，则进一步验证了非线性隔振系统应用是可能的，从而促进非线性隔振器的研究与应用，对于提高潜艇和鱼雷等水下航行器的声隐身性能具有一定的理论研究意义和军事应用价值。Duffing振子模型是非线性连续系统模型的典型代表，能很好地描述非线性隔振装置的动力学模型，带激励的Duffing振子因受激励的影响，会有超谐波和次谐波成分，在分岔过程中，也会有次谐波和超谐波分岔等现象，其动力学行为复杂而丰富。因此本题选取单自由度的非线性弹簧振子作为研究对象，建立数学模型，研究其丰富的动力学行为以及谱的变化规律。

2 非线性隔振系统模型

非线性隔振系统如图1所示，该系统的运动微分方程为

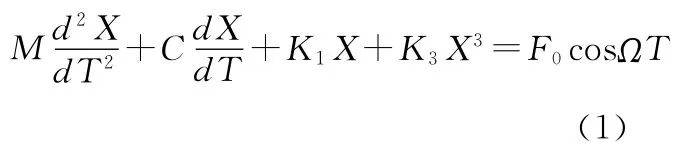
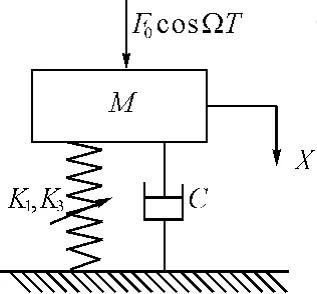
图1 非线性隔振系统

式中：K1X＋K3X3为非线性弹性回复力。

令

引入如下无量纲参数

则有

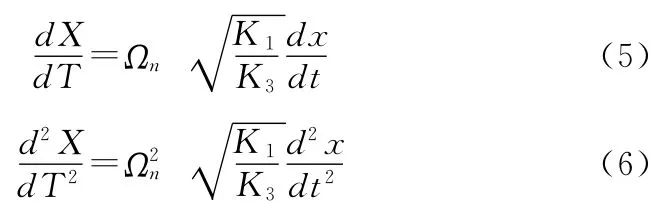
将式（2）～式（6）代入式（1），得

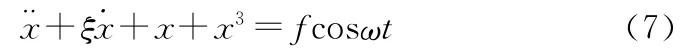
式（7）称为硬弹簧Duffing方程，式中：

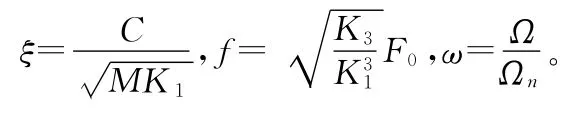
3 研究方法的选择

为了研究非线性系统的动力学行为，通常的方法有实验的方法和理论的方法。理论方法又分为定性方法和定量方法，定性方法主要研究系统的定性性质，如系统的分岔、周期解的稳定性和倍周期分岔等［8］；定量方法又分为解析方法和数值方法，大多数非线性系统很难求取精确解析解，所以常用的解析方法是近似解析方法，近似解析方法仅用于讨论系统的周期运动而无法表征混沌运动，对于混沌运动主要依靠数值方法［9～11］。带激励项的Duffing方程很难求取精确解析解，故本文将采用数值方法研究其功率谱特性。算法选用变步长的四阶龙格库塔法，用Mathematica计算软件模拟仿真。

4 谱特性研究

4.1 对称破缺分岔前谱特性

式（7）是对称系统，当系统的解为对称解时偶次谐波分量全为零，奇次谐波分量不全为零。主谐波响应是指与激励同频率的Fourier分量很大、而其它分量可忽略时的响应；n阶超谐波响应是指n倍激励频率的Fourier分量很大、而其它分量可忽略时的响应，主谐波响应和超谐波响应具有与外部激励相同的周期，故称为周期1解；如果响应周期是激励周期的m倍，则1／m和n／m倍激励频率的Fourier分量很大、而其它分量可忽略时的响应分别称为1／m次谐波和n／m超次谐波响应，这里m和n都是整数，称之为周期m解。图2为ξ＝0.1，ω＝2，f＝100时的功率谱图。初始位移、速度都为零。主谐波频率与激励频率相同，为1／π。除主谐波外，3，5，7阶超谐波同时存在，分别在频率为3／π，5／π，7／π处，峰值十分明显，并且由规律的排列，此时只有奇数阶超谐波，为周期1解，其相图是对称的，如图3所示。对称的周期1解都有相似的规律，各阶谐波在区间0.01≤ω≤1.2，的变化规律如图4所示，在0.01≤ω≤0.15和0.45≤ω≤1.1两个区间内3，5，7阶谐波增加和减小很平滑，功率谱都类似于图1，主谐波在区间上成增加趋势。

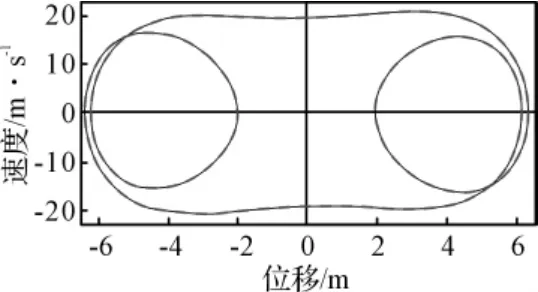
图3 参数ξ＝0.1，ω＝2，f＝100时的相图

4.2 对称破缺分岔后谱特性

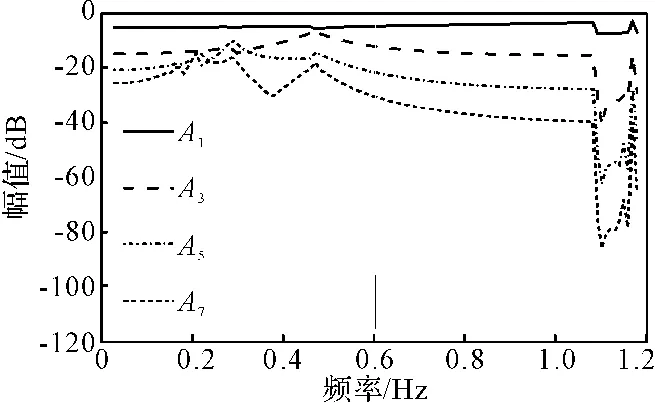
图4 参数ξ＝0.1，ω＝2，f＝100时的幅频曲线

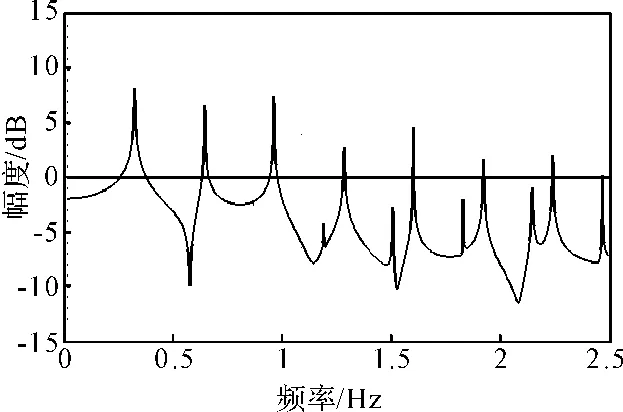
图5 参数ξ＝0.1，ω＝2，f＝92.55时的功率谱

图4表明在区间0.15≤ω≤0.45和1.1≤ω≤1.2出现不对称的解，与图2的功率谱特性有很大不同。如图5所示，偶数谐波出现，与图2相比较，偶数阶谐波出现在奇数阶谐波之间，相图失去对称性。图6是参数ξ＝0.1，ω＝2，f＝92.55时的相图，其中虚线表示轨线经过180°旋转后的位置。图5、图6表明偶数阶超谐波的出现是不对称轨道的标志。

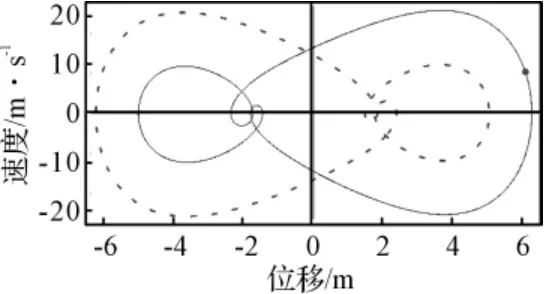
图6 参数ξ＝0.1，ω＝2，f＝92.55时的相图

4.3 次谐波分岔后谱特性

倍周期分岔的产物，如周期2解、周期4解等，都包含有偶数次次谐波，因而都是不对称的。由此不难推断，倍周期分岔都发生在轨线失去对称性的参数空间里，数值计算表明该推断是合理的，也就是说，对称性破缺分岔是倍周期分岔的前兆。

而周期3解存在对称解，如图7、图8所示轨线经过180°旋转后能重合，奇数阶次谐波不为零，偶数阶超谐波全为零。1／3次谐波峰值明显是周期3解的特点，1／3次谐波也发生了超谐波分岔，如图6所示5／3，7／3等谐波分量也不能忽略，偶数倍超谐波分量同样全为零，相轨线保持对称，如图8所示。

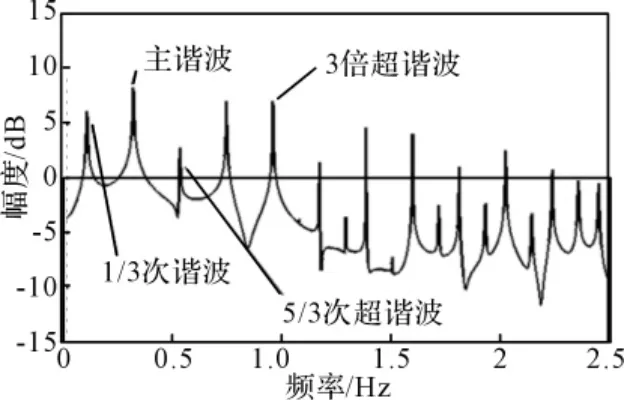
图7 参数ξ＝0.1，ω＝2，f＝78.77时的功率谱

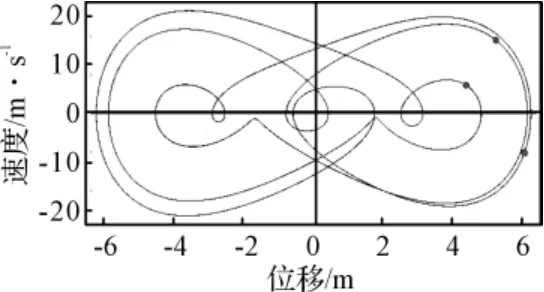
图8 参数ξ＝0.1，ω＝2，f＝78.77时的相图

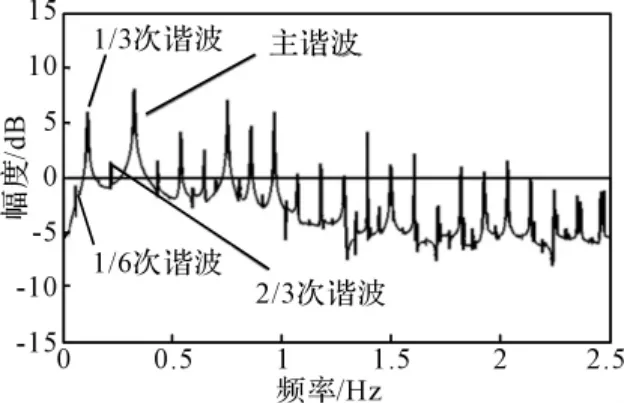
图9 参数ξ＝0.1，ω＝2，f＝57.79时的功率谱

图9表明1／3次谐波发生了倍周期分岔，由周期3的解变为周期6的解，同时有超谐波分岔，奇数阶和偶数阶超谐波分量不全为零，这表明次谐波分量也会和主谐波一样发生超谐波分岔和次谐波分岔，不断分岔将产生密集的谱线，最终成混沌的谱线，如图10所示，1，3，5，7阶超谐波分量十分明显，这说明混沌振动状态下蕴含着不稳定的周期轨道，谱线也是存在的。

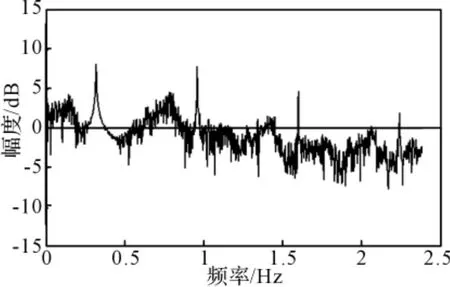
图10 参数ξ＝0.1，ω＝2，f＝92.54时的功率谱

5 结语

本文建立了一种舰船隔振装置的物理和数学模型，并对其进行了仿真计算，运用数值方法得到不同参数下的解，分析了这些解的功率谱特性，针对此模型得到以下结论：

1）对称破缺分岔前，功率谱为周期1 解，功率谱中只存在奇数阶超谐波，奇数阶谐波幅值成规则排列；

2）对称破缺分岔后，出现偶数阶超谐波分量，系统失去对称性，奇偶数阶超谐波都成不规则排列；

3）次谐波分岔后，次谐波也会出现超谐波分岔和次谐波分岔。

4）次谐波分岔不断产生新谱线，最终出现混沌，但奇数阶超谐波分量仍然是明显独立的谱线。

［1］朱石坚，何琳.舰船水声隐身技术［J］.噪声与振动控制，2002，22（34）：17-19.

［2］朱石坚，何琳.船舶机械振动控制［M］.北京：国防工业出版社，2006：160-161.

［3］Crede C E.Vibration and Shock Isolation［M］.New York：John Wiley ＆Sons，1951：20-33.

［4］楼京俊.基于混沌理论的线谱控制技术研究［D］.武汉：海军工程大学，2006：21-30.

［5］Feigenbaum M J.The Transition to Aperiodic Behavior in Turbulent Systems［J］.Communications in Mathematical Physics，1980，77：65-86.

［6］Feigenbaum M J.The Onset Spectrum of Turbulence［J］.Physics Letters A，1979，74（6）：375-378.

［7］Nauenberg M，Rudnick J.Universality and the Power Spectrum at the Onset of Chaos［J］.Physical Review B，1981，24（1）：493-495.

［8］刘延柱，陈立群.非线性振动［M］.北京：高等教育出版社，2001：2-4.

［9］吕永建.FFT 多谐波平衡法及其应用［D］.长沙：湖南大学，2012：7-13.

［10］李晓勇.基于强Duffing模型的隔振装置混沌特性参数研究［D］.广州：广州大学，2011：22-30.

［11］刘秉正，彭建华.非线性动力学［M］.北京：高等教育出版社，2004：99-106.

［12］杨夷梅，杨玉军.一种基于LDC混沌理论与RSA 的图像传输算法［J］.计算机与数字工程，2009，37（2）.