基于BRISK改进的快速角点特征算法＊

（1.海军航空工程学院兵器科学与技术系 烟台 264001）（2.91055部队6分队 台州 318050）

1 引言

在计算机视觉领域，区分性强、对多种几何及光照变化具有不变性的局部特征，特别是其中较为重要的角点特征，由于具有旋转不变性和不随光照条件变化而变化的特点，广泛应用于基线匹配、特定目标识别、目标类别识别、图像及视频检测、机器人导航、场景分类、纹理识别和数据挖掘等多个领域内。角点特征检测及描述算法一直是研究的热点［1～3］。

近几年，在满足对尺度、旋转，噪声具有鲁棒性的前提下，为了实时处理和降低硬件需求，特征检测匹配的研究重点为算法计算复杂性和内存占用量等方面。经过国内外学者的努力，已经有大量的速度较快且具有鲁棒性的相关算法，包括尺度不变性特征转换（SIFT）［4］，加速鲁棒特征（SURF）［5］，定向快速旋转Brief特征（ORB）［6］以及近期由Strfan等人提出的二值化鲁棒尺度不变特征（BRISK）［7］等。其中，BRISK 特征算子是一种新的具有尺度不变性和旋转不变性的角点检测和描述算法，与其他的特征检测与描述算法（SIFT，SURF等）相比，由于其采用二进制描述子以及Hamming距离匹配，使运算速度以及内存占用量有了明显改善。

本文首先对BRISK 中较为耗时的角点特征描述子建立算法进行改进，在提出采样点对选择策略后，不对BRISK算法中主方向确定，旋转，再采样的一系列过程进行计算，直接生成二进制串描述子；然后，在特征点匹配阶段，提出两步位操作特征匹配算法，为了加快算法执行速度，使用了部分匹配及检测汉明重量阈值的方法。实验结果表明，较原有的BRISK 算法，该改进方法具有更快的运算速度，更加满足嵌入式实时系统要求。

2 BRISK 算法

2.1 角点特征提取

BRISK 采用由Mair等人提出的AGAST 角点探测算法来提取角点特征。AGAST 算法又是对FAST（features from accelerated segment test）特征点检测算法的扩展，进一步提高了其运行速度。为此，本小节在分析FAST 的基础上，讨论其优缺点进而引出BRISK 对其改进之处。

FAST 特征检测算法来源于Corner的定义，这个定义基于特征点周围的图像灰度值。对于灰度图像来说，FAST检测候选特征点为圆心的离散化Breaenham 圆周上的像素值，如果候选点周围领域内有足够多的像素点与该候选点的灰度值差别够大（足够“亮”或足够“暗”），则认为该候选点为一个特征点［8］，如式（1）所示。

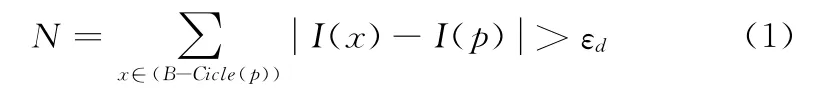
式中，x取值离散化Breaenham 圆周上的像素点，p为圆心点即候选角点，Ⅰ（x）为该像素点的灰度值，Ⅰ（p）为圆心像素点的灰度值，εd为给定的阈值。通过上式，可以求出圆周上满足式（1）的像素点个数N，当N大于某一阈值时，就可以判断该候选点为角点。为了获得更快的结果，还采用了额外的加速办法。从上面的分析可以看出，FAST 算法只利用周围像素比较的信息就可以得到特征点，运算简单，高效，实时性好。但显而易见的，FAST 也存在不可避免的缺点，包括：对噪声敏感，不具备旋转不变性以及不具备尺度不变性。

因此，为了去除噪声影响，BRISK 采用不同尺度高斯平滑去掉部分噪声干扰，通过使用FAST 值（FAST Score）作为度量局部最大性的指标，将点灰度测试转变为局部区域最值比较；为了具有尺度不变性，采用了多尺度AGAST 算法，在多尺度空间上，以FAST 值（FAST Score）作为显著性指标，寻找最值；为了适应旋转不变性，在描述子建立过程中，利用长距离点对的梯度累加估计角点主方向，并旋转角度。下面简单叙述BRISK 尺度空间关键点检测与描述子建立的基本思想。

2.2 尺度空间关键点检测

与其他具有尺度不变性的特征算法相同，BRISK 也是从构建尺度空间金字塔开始的。尺度空间金字塔由n层（octave）ci以及n-1个中间层（inter-octave）di（i＝1，2…）构成，中间层位于相邻两层之间，与SIFT 算法相同，文献［5］中n＝4。每一层从原始图像（对应于c0）开始由上一层0.5倍下采样得到，每一个中间层di位于层ci和层ci＋1之间。第一个中间层d0通过对原始图像c0进行1.5倍下采样，其他的中间层则是对上一个中间层进行0.5下采样得到。

关键点检测主要通过以下两步来实现。首先，具有相同阈值T的FAST 算子应用于每一层以及每一中间层，用于识别潜在的感兴趣区域。第二步，对这些潜在区域中的点在尺度空间进行非极大值抑制：1）在同一层待检测点FAST 值必须大于与它相邻的其他八个点；2）上一层和下一层的其他所有点的FAST 值都必须要低于该点的FAST值。满足这两个条件的点称为关键点。对于c0层的关键点检测，采用FAST-8关键点检测算法。考虑到图像显著性不仅对于图像是连续的，而且对于尺度维而言也是连续的。因此，对每一个检测出的极大值进行亚像素和连续尺度校正。亚像素级校正使用最小二乘意义上的2D 二次函数拟合，而连续尺度校正使用了沿尺度坐标拟合1D 抛物线的方法。在这里不展开叙述。

2.3 BRISK 描述子建立

受BRIEF 算法的启发，BRISK 也使用了由Calondor等人提出的二进制串［9］来描述每个特征点，其优点是采用汉明距离来计算匹配程度，即将特征先按位异或（XOR），然后统计结果中1的个数，若其较小，表明匹配程度较高。正如文献［7］证明的一样，这种算法在运算速度上比一般的欧式距离算法有明显优势。与其他二值化特征描述算法（如BRIEF，ORB等）不同，BRISK 不是利用随机点对，而是使用几个同心Bresenham 圆上均匀分布的点（如图1中所示的60个点，共计59×30＝1770个点对），由长距离采样点和短距离采样点对分别估计特征点方向和生成二进制描述子。

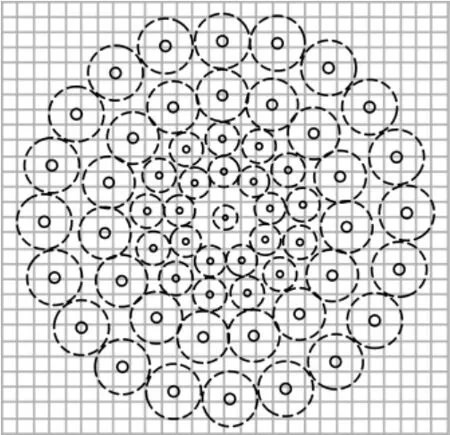
图1 BRISK 采样点分布

BRISK 描述子采用了邻域采样模式，即在以特征点为中心的每个离散化Breaenham同心圆上，取均匀分布的N个点。为了减少噪声的影响，利用标准差的高斯函数进行平滑滤波，标准差σ正比于每个同心圆上点之间的距离。考虑所有的采样点对构成的集合，记为A，如式（2）。所有采样点构成的点对中的一对，记为（pi，pj），平滑后的灰度值分别为Ⅰ（pi，σi）和Ⅰ（pj，σj）。定义短距离采样点对构成的集合S以及长距离采样点对构成的集合L如下

由于长距离采样点对包含更多的特征点角度信息，BRISK 利用两点之间的梯度g（pi，pj）公式（4），通过计算其总体模式方向为（5），旋转角度θ＝arctan2 （gy，gx）然后再次 采 样。设Ⅰ（Piθ，σi），Ⅰ（Pθj，σj）为旋转并高斯平滑后的采样点灰度值，通过短距采样点对按照式（6）就生成了二进制描述子。

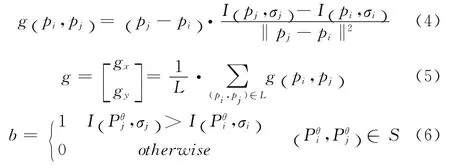
3 改进的BRISK 算法

3.1 改进原则

通过上面分析，BRISK 算法建立描述子过程涉及到点对选择，主方向确定，采样区域旋转，重采样等一系列阶段，所需时间较多。时间主要花费在如下两个阶段：一是描述子生成时，由于在待测特征点周围使用了较多的采样点（60个），造成采样点对数量较大，且相关性会比较大，从而降低描述子的判别性。通过降低采样点数，并优化点对选购策略是减少点对数量，降低相关性，提高算法速度的有效方法；二是为了满足旋转不变，通过远距离采样点对梯度和来确定主方向，然后又将特征点旋转，花费了大量的运算时间。实际上，依据主模式方向角度并旋转来实现旋转不变性，在特定场合（如连续图像序列）是不必要或是精度要求较低的。另外，Calonder在文献［9］中也指出，角度方向的检测过程还会减低后续图像识别过程中的识别率。同时，在实际的嵌入式运行环境中，一般设备，如便携电子设备（手机、平板电脑等）或是军用设备上，均可以通过其他传感器获得视点变化带来的特征方向角度信息。为此，本文在生成描述子的同时，只根据特征点周围距离较远的点来生成粗略的角度信息。

3.2 特征描述子建立

3.2.1 点对选择策略

文献［10］中FREAK 算法模拟人眼功能，利用不同标准差高斯函数构建平滑重叠区域，中间密集，四周稀疏，模拟人眼视网膜细胞的分布，减少采样点数量，进而减少用于建立特征描述子的点对数量。由BRISK 的60 个采样点（59×30＝1770对）变成43个采样点（43×21＝903对）。在提高速度的同时，内存占用量也大大降低。本文也采用其定义的“视网膜”采样区定义的43个采样点，如图2。

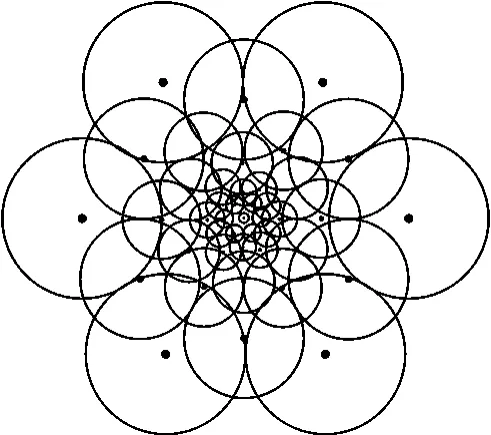
图2 FREAK 采样区域

点对选择策略上，BRISK 将所有属于短距离采样点对均进行了计算，进而生成二进制串，带来的问题是采样点对具有较高相关性。为此，在ORB 算法中，离线下计算测试数据，利用小相关性（均值0.5）的方法得到点对选择策略。按照上面思路，对测试图像中的采样点，首先构建二维矩阵，矩阵每一行为某点遍历其他所有采样点形成的二进制描述子；然后考虑该矩阵的每一列，只有其均值在0.5附近，表明该列的0，1分布数量较为相同，该采样点对相关性低。据此，按照均值排序，选择相关性较低的点对组成。最终，选择了排序后相关性较小的前128个点对。

3.2.2 双二进制串描述子

双二进制串描述子指的是特征点幅度和角度二进制描述子。在尺度空间关键点检测后，得到关键点坐标，然后利用FREAK 使用的高斯函数，对“视网膜”采样区进行平滑，再选择上述离线确定出的128个点对，不经过主模式确定及旋转过程，直接按照式（7）生成128维特征点二进制描述子，其中，Ⅰ（Pi，σi），Ⅰ（Pj，σj）为高斯平滑后的采样点灰度值，A128为128个点对构成集合。由于该描述子反映的是特征角点周围采样区域的灰度情况，称它为特征点幅度二进制描述子。

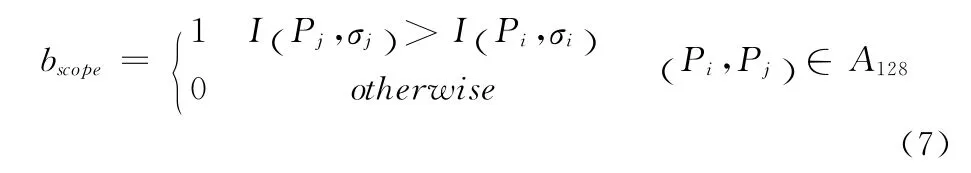
通过上面方法生成的特征点二进制描述子中，较远距离采样点对数量无法确定，导致其中含有的特征点角度信息不明显，如果据此通过下面介绍的循环移位指令直接模拟角度旋转，并进行特征点匹配，有可能造成角度信息匮乏使误配较高。为此，本文在采样区高斯平滑后，于关键点周围64个采样点中，选取距离较远的点，同关键点组成点对，比较灰度生成特征点角度二进制描述子。这里，以顺时针方向，按照距离中心位置远近，从远至近，从关键点正上方开始，顺时针依次提取18 个采样点。图3中为了直观显示，提取点位于不同半径Bresenham 黑色圆点，高斯平滑区域用不同颜色表示。采样点加上关键点共19点，形成点对规模为19×9＝171，同样按照上文描述方法，离线找到相关性较小的128对点，按照式（8）生成128位二进制角度信息数据，其中Ⅰ（P0，σ0）为关键点（图3中心点）平滑后的灰度值。

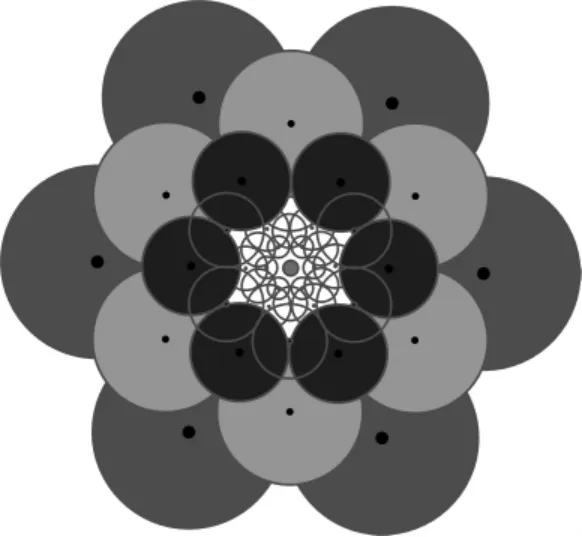
图3 计算角度二进制描述子所用的采样区域

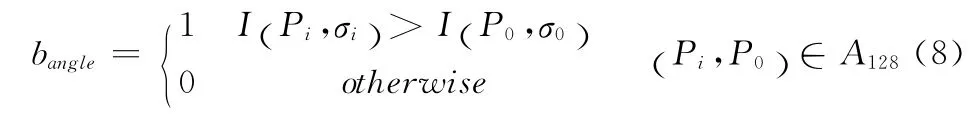
3.3 特征匹配算法

3.3.1 两步位操作特征匹配算法

通过上面建立的双二进制串描述子，设待匹配两个特征点（Pa，Pb）的特征点幅度和角度二进制描述子分别为

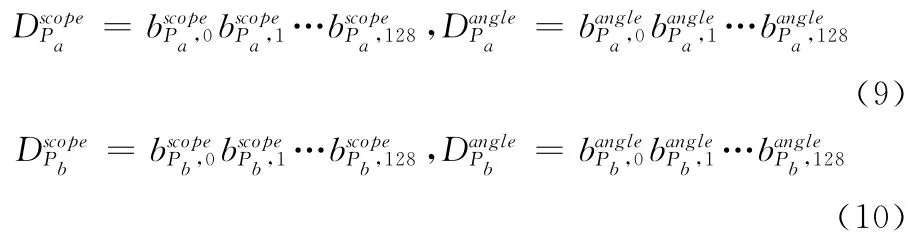
本文建立的两步位操作特征匹配算法Two Step Bits Operation Matching（TSBOM）。按照时间先后的两步骤是指旋转角度匹配位操作与特征幅值匹配位操作。其核心是在考虑尺寸变换基础上，考虑到采样点均匀分布在同心Bresenham 圆上，将角度二进制描述子按位循环位移来模拟角度旋转。具体来说，对于角度描述子，共需移位128次，每循环移位后，计算两个特征点角度汉明距离，找到最匹配（即最小距离）位移操作位数（即旋转角度信息）M，然后移动幅度描述子M次，再完成两个特征点幅值匹配工作。如式（11），（12）所示，其中函数Fi（）表示对二进制串循环左移i次，⊗为按位“异或”操作。

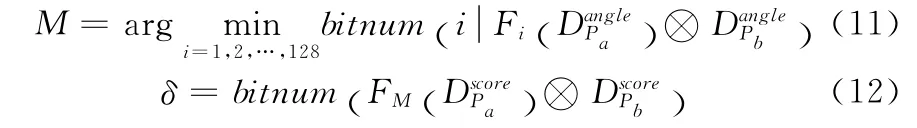
3.3.2 优化方法

1）汉明重量阈值

若两幅图像中，两个特征点为匹配点，不论如何按位“移位”（旋转），不考虑噪声干扰，在一定误差情况下，二者上述两种描述子中1的个数相近，否则可以判定不为匹配点。汉明重量是字符串中非零的元素个数，对于二进制字符串，是指其中1的个数，设统计字符串中汉明重量的函数为FHWeight（）。设置差异度函数为的定义按照式（13）），若此值大于设定的阈值（本文为7），则两特征点不为匹配点，不需进行如下的移位，再匹配等指令，降低了运算量。

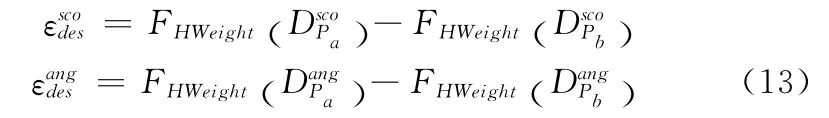
2）部分描述子匹配

TSBOM 算法含有多位二进制运算，能否只比较256位中的部分，来剔除大量待匹配点，进而降低位运算总次数，有效提高算法运算效率？其实，按照提取策略，提取顺序靠前的点对，相关性最小，最具有辨别力，其对应双二进制串描述子的前几位。为此，对每个待匹配特征点，预处理128位幅值描述子的前几位，可以剔除大量的待匹配点，达到加速目的。大多数CPU，一个指令周期就能完成16位的二进制操作。由此，使用幅值描述子的前16位，作为“预先”匹配描述子。

4 实验结果及分析

实验程序使用最新公布的OPenCV 2.4版本，实验硬件平台为Intel Pentium E5300，2G RAM，开发环境使用Visual Studio 2010，测试的图像来自于Computer Vision Laboratory图像测试数据库（http：／／www.robots.ox.ac.uk／～vgg／research／affine／）。将SIFT，SURF，BRISK 及本文算法速度进行了对比，使用典型的castle，fountain以及herzjesu图像库中的两幅图像，统一进行缩放，计算平均耗时，结果如表1所示。由于BRISK 与本文算法均使用了尺度空间关键点特征点检测算法，因此，检测的特征点数量以及检测耗时均较为相近，而FAST 算法只利用周围像素比较的信息就可以得到特征点，运算简单，高效，比SIFT 和SURF在速度上有了大幅提高。在描述子生成阶段，与SIFT 或SURF 不同，BRISK 与本文算法只是利用点对选择策略，通过比较高斯平滑后的灰度值，速度也有明显提升。而本文算法，由于省掉了原BRISK 算法中主方向计算，旋转，再采样的一系列过程，直接生成二进制串描述子，速度提升将近一倍。在匹配阶段，BRISK 与本文算法均使用二进制汉明距离，通过位操作完成匹配，较SIFT 以及SURF速度快。在匹配阶段，本文算法由于涉及到两步位操作，执行速度有所降低，但使用了改进的加速算法后，通过部分匹配及检测汉明重量阈值的预先处理过程，剔除了大量的非匹配点，提高了执行效率，与BRISK 匹配速度基本一致。最终，由本文算法匹配的图像如图4所示。总体耗时水平上，本文算法更具速度优势，如表1所示。

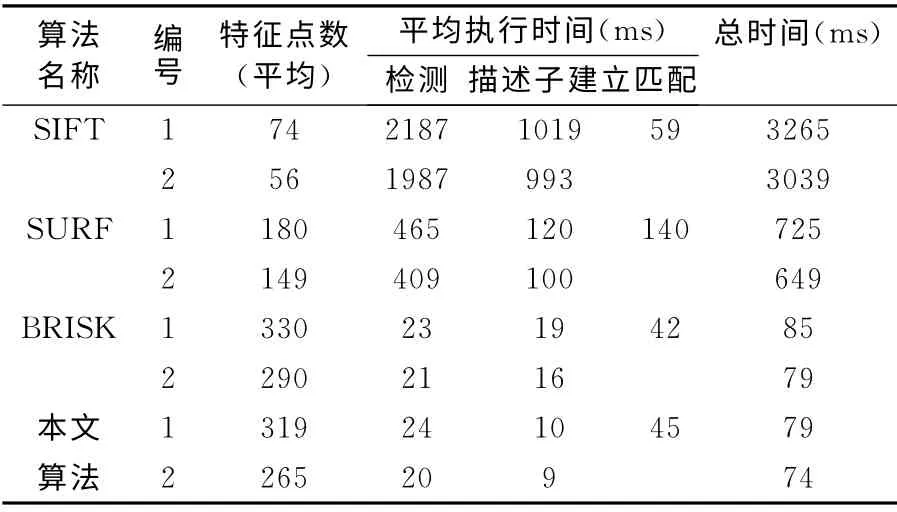
表1 算法效率对照表

5 结语

本文改进了BRISK 中较为耗时的角点特征描述子生成算法，提出了采样点对选择策略和幅值-旋转两级描述子建立方法；另外，在特征点匹配阶段，提出两步位操作特征匹配算法，并通过部分匹配及检测汉明重量阈值的方式进一步加快算法执行速度。实验结果表明，较原有的BRISK算法，该改进方法由于剔除了描述子建立阶段的主模式确定及旋转过程，因此具有更快的运算速度，更加满足嵌入式实时系统要求。

［1］孙浩，王程，王润生.局部不变特征综述［J］.中国图象图形学报，2011，16（1）：141-151.

［2］章为川，程冬，朱磊.基于各向异性高斯核的多尺度角点检测［J］.电子测量与仪器学报，2012，26（1）：37-43.

［3］马芳芳，徐天乐.图像特征提取算法仿真研究［J］.计算机仿真，2012，29（8）：227-230.

［4］Mikolajczyk，schmid.Scale ＆affine Invariant Interest Point Detectors［J］.International Journal of Computer Vision，60（1），2004：63-86.

［5］H.Bay，T.Tuytelaars，and L.Van Gool.SURF：Speeded up robust features［C］／／In Proceedings of the European Conference on Computer Vision（ECCV），2006：1113-1126.

［6］Ethan Rublee，Vincent Rabaud，Kurt Konolige，Gary R.Bradski：ORB：An efficient alternative to SIFT or SURF［C］／／In Proceedings of the IEEE International Conference on Computer Vision（ICCV），2011：318-327.

［7］Stefan Leutenegger，Margarita Chli and Roland Siegwart，BRISK：Binary Robust Invariant Scalable Keypoints［C］／／In Proceedings of the IEEE International Conference on Computer Vision（ICCV），2011：269-279.

［8］E.Rosten and T.Drummond.Machine learning for high speed corner detection［C］／／In Proceedings of the European Conference on Computer Vision（ECCV），2006：412-429.

［9］M Calonder，V Lepetit，C Strecha，P Fua.BRIEF：Binary Robust Independent Elementary Features［C］／／In Proceedings of the European Conference on Computer Vision（ECCV），2010：812-826.

［10］A.Alahi，R.Ortiz，P.Vandergheynst.FREAK：Fast Retina Keypoint［C］／／In IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2012：263-286.