基于EMD－BP神经网络的我国棉花期货价格预测方法研究＊

王伟国，赵新民

（石河子大学 经济与管理学院，新疆 石河子832003）

一、引 言

棉花是重要的农作物，也是重要的工业原料，棉花价格是棉花行业发展乃至国民经济运行中的重要经济变量，棉花价格水平的高低，直接影响棉花生产、流通、加工和消费，与农村经济、纺织工业经济正常运行均具有较大联系，棉花价格过低或过高都会对棉花产业及国民经济系统稳步持续发展产生不良影响。1999年，我国棉花价格放开后，由政府发布预测性的价格信息，是市场经济条件下政府调控市场、引导价格的有效方式。这也是发达市场经济国家的普遍做法。正确把握棉花价格运行规律，预测棉花价格走势是深化棉花流通体制改革、提高政府决策水平的必然要求，已成为我国农业经济领域研究的重要内容。

当前，许多经济学家围绕棉花价格问题展开了大量研究。张立杰、朱新杰（2012）通过HP滤波分析了我国棉花价格的长期走势，并在分析2008－2011年间月度棉花价格的基础上建立了基于差分自回归移动平均ARIMA（1，1，1）的棉花价格预测模型，利用该模型预测了2012年1月至4月间棉花价格，结果显示，ARIMA（1，1，1）模型能够较好地模拟并预测短期国内棉花价格［1］。刘晓雪、张悦（2012）基于供求、货币流动性和其他因素理论分析了棉花价格波动的原因后，运用协整检验、格兰杰因果分析实证研究了库存信息和货币流动性变动对棉花期货价格波动的影响程度［2］。王利荣、周曙东（2009）运用协整检验、误差修正模型及脉冲响应函数等方法分析了我国加入世贸组织后国内棉花价格与国际棉花价格之间的动态关系，国内棉价与国际棉价具有长期均衡关系，其中国际棉价波动对国内棉价有较强的冲击，对国内市场起引导作用，而国内棉价波动对国际市场影响较小［3］。李琴、孙良媛（2005）基于向量自回归模型，构建1978－2002年我国棉花进口、库存和价格相互作用的动态模型，分析了棉花进口、库存和价格之间的因果关系，认为棉花价格、库存和进口三者之间的相互影响存在一定的时滞，这种时滞是导致它们出现几乎协同性的周期性波动的根本原因［4］。周曙东（2001）研究认为，长期以来，我国棉花的生产和流通一直处在波动之中，棉花价格忽升忽降，卖棉难和买棉难交替出现，棉花生产大起大伏。棉花价格、产量、供求关系的巨大波动，显然不利于我国棉花和纺织业生产的稳定发展，1999年的棉改并没有解决供求波动的问题［5］。据此可见，学者们利用线性回归模型、ARMA模型、协整理论等计量方法，对棉花价格问题进行了系统的研究，都在一定程度上解释了棉花价格的波动情况，但关于棉花价格走势的预测精度有待进一步提高。本文尝试运用EMD和神经网络组合方法对棉花期货价格进行预测分析，以改进棉花价格走势预测方法，提高预测精度。

二、EMD方法简介

EMD（emprirical Mode Decomposition），又称“经验模式分解方法”，它的优点是能够对非线性、非平稳过程的数据进行线性化、平稳化处理，分解的最终函数彼此之间是正交的，从而在分解的过程中尽可能地保留数据本身的特性［6］。

EMD的基本思路是用波动上、下包络的平均值确定“瞬时平衡位置”，进而提取内在模函数（IMF），记为I（t）。其计算过程主要有3个步骤：1.找出原序列F（x）的各局部极大值，用三阶样条函数插值，得到原序列F（t）的上包络序列值Fmax（t）。同理可以得到下包络序列值Fmin（t）。2.对每个时刻的Fmax（t）和Fmin（t）取平均，得到瞬时平均值 m（t）：m（t）＝［Fmax（t）＋Fmin（t）］/2。3.用原序列F（t）减去瞬时平均值m（t），得到类距平均序列h（t）：h（t）＝F（t）－m（t）。

若h（t）中极值点的数目和跨零点的数目相等或至多只差一个，并且各个瞬时平均值m（t）都等于零，则它是内在模函数，否则，把h（t）当作原序列，重复以上步骤，直到满足内在模函数的定义，求出内在模函数为止。求出第一个内在模函数I1（t），即从原序列分解出第一个分量。然后用原序列减去I1（t）得到剩余值序列r1（t）：r1（t）＝F（t）－I1（t）。至此提取第一个内在模函数的过程完成。然后，把r1（t）作为一个新的原序列，按照以上步骤，依次提取第二、第三……直到第n个内在模函数In（t）。rn（t）变成一个单调函数序列，再没有内在模函数能被提取出来。如果把分解后的各分量合并起来，就得到原序列F（t）：F（t）＝∑Ii（t）＋rn（t），其中Ii（t）为各IMF分量，rn（t）为趋势项。

三、基于EMD的BP神经网络预测模型

（一）BP神经网络

神经网络用于时间序列预测，是指利用神经网络去逼近一个时间序列，可用时间序列的前k个值Xn，Xn－1，…，Xn－k－1去预测以后的 m 个值 Xn＋1，Xn＋2，…，Xn＋m，描述为：Xn＋m＝F（Xn，Xn－1，…，Xn－k－1），即用神经网络来拟合函数F，并用它来推导未来的值。当m等于1时，是一步预测，网络输出个数为1；当m大于1时，是多步预测，每次可计算出多步预测值。

典型的BP网络是三层网络，包括输入层、隐含层和输出层。BP网络的学习由四个过程组成：输入模式由输入层经中间层向输出层的“模式顺传播”过程；网络的希望输出与网络实际输出之差的误差信号由输出层经中间层向输入层逐层修正连接权的“误差逆传播”过程；由“模式顺传播”与“误差逆传播”的反复交替进行的网络“记忆训练”过程；网络趋向收敛即网络的全局误差趋向极小值的“学习收敛”过程。简言之，就是由“模式顺传播”→“误差逆传播”→“记忆训练”→“学习收敛”的过程。BP网络通常有一个或多个隐层，隐层中的神经元均采用S型交换函数，输出层的神经元采用纯线性变换函数。

（二）预测模型

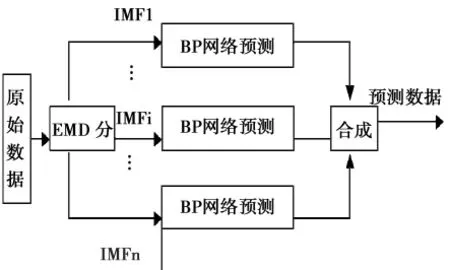
图1 基于EMD的BP神经网络预测模型

基于EMD的BP神经网络的预测模型如图1所示。模型预测具体步骤如下：1.采用EMD分解，将非平稳数据分解为不同尺度的平稳的IMF分量；2.将各IMF分量送入BP神经网络进行预测，对每个时间序列都力求选取合适的输入层和隐层神经元个数，从而达到最佳的预测效果；3.所有网络输出后用各个分量的预测值重构原始数据的预测序列。

三、实证分析

本文数据来自大智慧证券信息港—郑州商品—郑棉连续（CF0001）从2011年2月16日至2012年2月23日之间的交易日收盘价，共200个样本数据，对数据作归一化处理检验。用matlab软件对时间序列数据编程建模与预测。EMD分解后产生7个分量，通过输入层节点和隐层节点调试法，分别得到7个网络结构：10－13－4，4－11－1，10－8－1，4－6－1，11－7－1，12－9－1，12－10－1。为了比较本方法的实验效果，对原始数据直接用BP网络预测，调试出最好网络结构为12－10－1。

基于上述模型，外推5个样本，将模型的预测值与实际值进行比较，具体结果见表1。同时，为了显示组合模型的优越性，并将单纯BP网络的预测结果也列入表1。

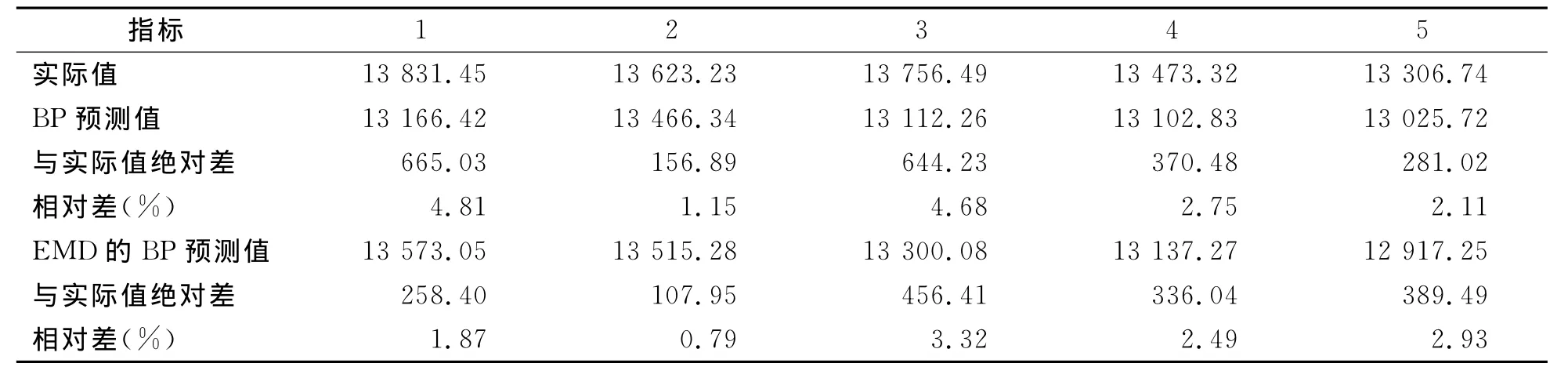
表1 预测结果的比较

表1显示，在外推的5个检验样本中EMD的BP网络预测的平均相对误差仅有2.28%，明显小于单纯BP网络预测平均相对误差3.1%。因此，EMD的BP网络组合模型的预测精度要高于单纯的BP网络模型。

四、结 论

针对我国棉花期货价格时间序列数据非线性和非平稳性的特点，本文采用了一种全新的预测方法，即基于经验模式分析（EMD）的BP神经网络预测模型。该方法首先将原始时间序列数据用EMD技术进行分解，然后对分解后的平稳序列按照不同频率设计出合理的BP神经网络模型进行预测，最后对不同频率序列BP神经网络预测结果进行重新组合，得出时间序列数据的预测值。

通过对我国棉花期货价格数据分别利用EMD－BP神经网络模型和单纯的BP神经网络模型进行了实证研究，结果表明：EMD－BP神经网络模型较传统的BP神经网络模型更具有效性，拟和与预测精度明显提高。因此，这一方法既可以克服单纯利用EMD预测方法的建模复杂程度，同时可以提升BP神经网络模型的预测精度。

另外，鉴于EMD技术分解的特点，可以将非平稳时间序列分解成若干平稳时间序列，因此，它可以与其他多种预测方法组合使用，这样可以使预测误差进一步降低，预测精度进一步提高。EMD技术分解方法有广泛的应用前景，有助于推动经济预测与决策问题的深入研究，同时也能推动预测理论的进一步发展。

［1］张立杰，朱新杰.我国棉花价格长期走势与短期预测——基于差分自回归移动平均模型（ARIMA）的分析［J］.价格理论与实践，2012，（6）：53－54.

［2］刘晓雪，张悦.我国棉花价格异常波动原因的实证研究——基于库存信息和货币流动性视角［J］.价格理论与实践，2012，（4）：65－66.

［3］王利荣，周曙东.国内外棉花市场价格的动态关系分析——基于 VECM 模型［J］.国际贸易问题，2009，（11）：26－31.

［4］李琴，孙良媛.棉花价格、进口及库存的互动关系［J］.中国农村经济，2005，（7）：71－77.

［5］周曙东.中国棉花长期波动的规律及深层次原因［J］.农业经济问题，2001，（6）：44－48.

［6］刘海飞，李新丹.基于EMD方法的股票价格预测［J］.统计与决策，2011，（10）：59－61.