钢筋混凝土桥承载力安全储备综述

高 承 李 青 程玉平

（武汉建筑质量监督站 湖北 武汉：430000）

0 引言

桥梁作为土木工程结构的重要组成部分，具有投资数额大、服役时间长、地位关键等特点，在整个交通运输网的合理规划与安全运营中起着举足轻重的作用，也是国家重点投资建设的基础设施之一。因此，桥梁结构应选择合理的安全储备。由于公路桥梁与铁路桥梁在设计方法上存在差异，故本文对两种桥梁的安全储备分别进行了讨论。

1 安全储备基本概念

1.1 安全储备指标

实际桥梁结构存在荷载作用、材料参数、几何尺寸以及计算模式等方面的不确定性［1－2］，故其需要具有一定的安全储备。

结构安全储备是指结构和构件在遭受意外超载和意外事件时极限破坏状态与设计目标状态的比值［3］。在设计过程中，承载力储备是采用的最主要的安全储备指标，其表达式为：

式中，Cu、Cd分别为结构的最大承载力和设计承载力。

1.2 确定安全储备的综合因素

确定结构的安全储备，应考虑到国家和社会的经济、技术水平，结构的生命周期，结构的功能需求及重要程度，另外还需考虑到增加安全储备与增加费用之间的关系。

2 铁路桥梁安全储备

2.1 容许应力法

现行的铁路桥涵设计规范采用的是容许应力法［4－5］。容许应力法是以构件带裂缝工作阶段的应力状态为计算依据，将钢筋混凝土看作完全弹性体，应用材料力学匀质体公式，算出结构在标准荷载下的应力，并要求任一点的应力，不超过某一确定的容许值。材料的容许应力，是由材料的屈服强度或极限强度除以安全系数而得。即

式中，fk为钢筋的屈服强度或混凝土的极限强度；K为安全系数。

2.2 安全系数

容许应力法用安全系数K使构件强度（承载能力）有一定的安全储备，但K的取值是经验性的。该系数与结构的类型、荷载组合等因素有关［4－5］。

轴心受压是以混凝土的抗压极限强度除以安全系数2.5得出；弯曲受压及偏心受压的安全系数采用2.0，主要考虑应力图形为三角形，仅外纤维应力达到容许值，因此安全系数可适当降低；有箍筋及斜筋时的主拉应力是以混凝土的抗拉极限强度乘以系数0.9得出；无箍筋及斜筋时的主拉应力的安全系数采用3.0；梁部分长度中全由混凝土承受的主拉应力的安全系数采用6.0；纯剪应力的安全系数采用2.0；光圆钢筋与混凝土之间粘结力的安全系数采用2.4；局部承压应力考虑应力提高系数β，β是根据混凝土套箍强化理论推导而来。

考虑到不同荷载同时发生的几率不同，因此不同荷载组合时结构物应有不同的安全储备，采用的安全系数应该有所区别，反映在设计上的材料的容许应力也应不同。对于主力作用下的安全系数要求高一些；对于附加力和特殊荷载则可低一些。规范中以主力时的容许应力或安全系数为基数，对其他的荷载组合可将容许应力分别乘以不同的系数，或采用不同的安全系数，见表1。

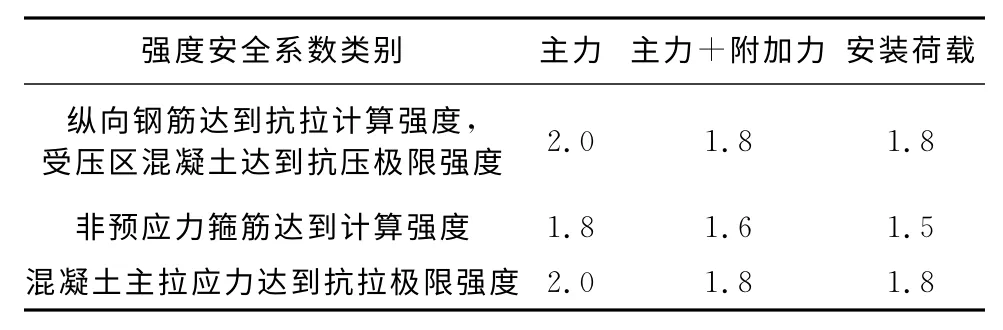
表1 容许应力法安全系数

但是由于单一安全系数是一个笼统的经验系数，因之给定的容许应力不能保证各种结构具有比较一致的安全水平，也未考虑荷载增大的不同比率或具有异号荷载效应情况对结构安全的影响。往往造成只是材料强度安全系数的错觉，结构荷载（或效应）的安全系数应该分配多少是一个未知数，因此常常拿现行列车荷载（轴重）与设计列车荷载标准像比较，认为标准荷载储备不足。在荷载组合上经常将可同时出现的荷载（或效应）的最大绝对值相叠加进行设计，在一些设计状况下设计可能太保守，而在另一些设计状况下可能安全储备不足［6］。

3 公路桥梁安全储备

3.1 极限状态法

现行的公路桥涵设计规范采用的是极限状态法［7－8］。整个结构或结构的一部分超过某一特定状态而不能满足设计规定的某一功能要求，则此特定状态为该功能的极限状态。对于公路桥梁需要对其承载能力极限状态和正常使用极限状态分别进行考虑。本文仅介绍承载能力极限状态，其定义为对应于桥涵结构或其构件达到最大承载能力或出现不适于继续承载的变形或变位状态。作用效应基本组合表达式［7］：

式中，Ψc为除汽车荷载外其他可变作用效应的组合系数；γ0、γs、γGi、γQ1、γQj和γf均为分项系数；R（，）为构件承载力函数。

3.2 分项系数及组合系数

式（3）是国内外较普遍采用的公路桥梁结构承载能力极限状态设计的通式。如式（3）所示，以可靠性理论为基础的极限状态设计一般采用带有分项系数的极限状态设计表达式，式中的设计基本变量通过概率分析取其代表值，而以分项系数来反映它们的变异性。可见，公路桥梁结构的安全储备体现在组合系数以及各分项系数上。

3.2.1 组合系数ΨC

在作用效应组合中，由于几个独立可变作用效应最不利值同时出现的概率较小，因而引入效应组合系数ΨC对作用进行折减，其值与作用效应组合中除汽车荷载外其他可变作用的数量有关，如表2所示。

表2 作用效应组合系数

3.2.2 结构重要性系数γ0

公路桥梁根据结构破坏可能产生的后果的严重性程度划分为三个设计安全等级，结构重要性系数γ0按结构不同安全等级采用，如表3所示。

表3 公路桥涵结构的结构重要性系数

3.2.3 作用效应和结构抗力计算模式不定性系数γS和γR

公路桥梁在统计分析中已纳入各自的分项系数，可取γS＝γR＝1.0。

3.2.4 永久作用分项系数γG

公路桥梁恒载效应的分项系数γG的取值，视永久作用效应对结构承载能力的利弊而定，其具体取值如表4所示。

表4 永久作用效应的分项系数

3.2.5 可变作用分项系数γQ

汽车荷载在公路工程结构中通常被视为主导的可变作用，在设计表达式中与永久作用一样单独列出。在桥梁设计中，汽车荷载效应（含汽车冲击力和离心力）的分项系数取γQ1＝1.4。当某个可变作用在效应组合中其值超过汽车荷载效应时，则该作用取代汽车荷载，其分项系数采用汽车荷载的分项系数；对于专为承受某作用而设置的结构或装置，设计时该作用可被视为主导作用，分项系数取与汽车荷载同值；计算人行道板和人行道栏杆的局部荷载，其分项系数也与汽车荷载取同值。

除汽车荷载效应、风荷载外的可变作用效应的分项系数γQj＝1.4，风荷载效应的分项系数γQj＝1.1。

3.2.6 结构材料性能分项系数γf

结构抗力分项系数γR不能直接用于设计，需将其转化为材料性能分项系数γf来表达。

4 算例分析

为了对比铁路和公路桥梁承载力安全储备的差别，以跨度为10m，截面宽200mm、高450mm，配置3根直径18mm 钢筋的普通钢筋混凝土简支梁为例，不考虑温度、收缩徐变等作用，将活载假定为集中荷载，简要分析如下。

4.1 安全储备指标

以跨中截面弯矩为研究对象，则式（1）中表达的安全储备指标将变为

式中，Mu、Md分别为跨中截面能承受的最大弯矩和设计弯矩。

以跨中集中荷载为研究对象，则式（1）中表达的安全储备指标将变为

式中，Fu、Fd分别为跨中集中荷载的极限值和设计值。

4.2 极限破坏值

4.2.1 极限破坏弯矩

对于给定的截面，材料性能、截面尺寸、钢筋数量及布置为已知，最大承受的正截面弯矩也是一个定值，其近似计算公式［9］

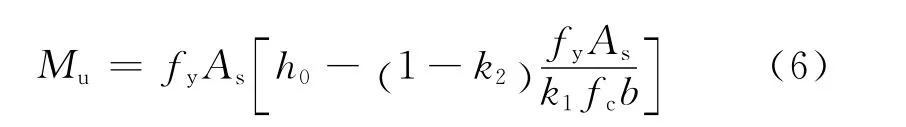
式中，fy为钢筋的屈服强度；fc为混凝土轴心抗压的极限强度；As为钢筋面积；h0和b分别为截面的有效高度和宽度；k1和k2为混凝土受压应力－应变曲线系数，取值如表5所示。

表5 混凝土受压应力－应变曲线系数

4.2.2 极限破坏时荷载

忽略塑性对荷载的影响，则跨中集中荷载最大值如式（7）所示。

式中，l为跨度，qG为结构自重产生的均布荷载。

4.3 铁路桥梁最大设计值

4.3.1 最大设计弯矩

根据容许应力法的计算图示，结合材料力学公式及截面几何关系可以得到已知截面的最大设计弯矩

式中，n为钢筋的弹性模量与混凝土的变形模量的比值，与混凝土强度等级，对于桥跨结构，C20混凝土取20，C25～C35混凝土取15，C40～C60混凝土取10。

当混凝土最外缘的压应力达到了容许值［σc］，而钢筋的拉应力σs＜［σs］，式（8）中最大设计弯矩Md变为

当钢筋的拉应力达到了容许值［σs］，而混凝土最外缘的压应力σc≤［σc］，式（8）中最大设计弯矩Md变为

4.3.2 最大设计荷载

跨中集中荷载最大值如式（11）所示。

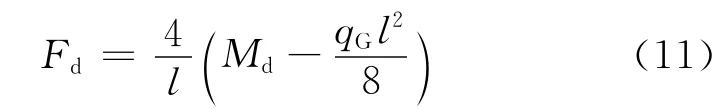
4.4 公路桥梁最大设计值

4.4.1 最大设计弯矩

普通钢筋混凝土正截面承载能力的公式如下：

受压区高度x根据力的平衡求得，即

式中，fcd、fsd分别为混凝土和钢筋的设计强度。

4.4.2 最大设计荷载

跨中集中荷载最大值如式（14）所示。

4.5 计算结果

选用不同强度的混凝土及钢筋，计算相应的安全储备，结果如图1所示。图中，公路1、公路2、公路3对应的结构重要性系数γ0取值分别为0.9、1.0、1.1。图1（a）、图1（c）为弯矩安全储备，图1（b）、图1（d）为荷载安全储备。

图1 安全储备计算结果

从图1中可以看出，对于跨中截面弯矩，铁路简支梁的安全储备比公路简支梁的高，而对于跨中集中荷载，铁路简支梁的安全储备却不一定大于公路简支梁的，这主要是由于弯矩安全储备的计算过程中，没有考虑荷载的安全系数。同时，公路桥梁规范重结构的安全等级越高、其结构重要性系数越大，对应的安全储备也越高，。

另外，对比图1（a）、1（c）并对比图1（b）、1（d），根据公路桥涵计算出的两种安全储备，随着钢筋强度的提高，其值略有提高；随着混凝土强度等级的增大，安全储备却降低，但是变化的幅度也十分小。而根据铁路桥梁计算出的安全储备却规律不明显，存在波动，甚至如图1（c）、1（d）所示，对于低强混凝土，其值变化很大。

5 结论

铁路和公路钢筋混凝土桥梁，由于设计方法的不同，使得安全储备的表现形式存在差异。通过对比可知，铁路桥梁采用容许应力法设计，用单一安全系数来表征桥梁的安全储备，简洁明了，但是安全系数是一个笼统的经验系数，故给定的容许应力不能保证各种结构具有比较一致的安全水平，而且没有反映材料的塑性特征，计算结果偏于保守。而公路桥梁采用极限状态法，用一系列分项系数来表征桥梁的安全储备，这些系数经可靠度校准并参考以往设计经验综合分析得到，每项系数的概念较为明确，且针对不同安全等级的结构，采用不同的安全储备值，经济性更好。

［1］张业平.连续梁桥结构体系的可靠度研究［D］.合肥：合肥工业大学.

［2］贡金鑫，魏巍巍.工程结构可靠性设计原理［M］.北京：机械工业出版社，2007

［3］叶列平，林旭川，冯 鹏.高强钢筋混凝土梁受弯承载力安全储备及经济性分析［J］.建筑结构，2006，36（6）：72－75.

［4］TB10002.1－2005.铁路桥涵设计基本规范［S］.北京：中国铁道出版社，2005.

［5］TB10002.3－2005.铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.北京：中国铁道出版社，2005.

［6］李铁夫.铁路桥梁可靠度设计［M］.北京：中国铁道出版社，2006.

［7］JTG D60－2004.公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.

［8］JTG D62－2004.公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［9］叶列平.混凝土结构（上册）［M］.北京：清华大学出版社，2006.