双输入型模糊前向神经网络的构建

杨文光，闫守峰，文小艳

(华北科技学院基础部，中国 北京 101601)

目前，前向神经网络是应用最为广泛，研究最为成熟的一种人工神经网络模型．由于这种神经网络构造相对简单，且有效地解决了非线性目标函数的逼近问题，而被大量的应用于模式识别、系统辨识、信号处理和自动控制等学科领域中[1-3]．与模糊系统的结合应用，使得作为神经网络构成要素的激励函数、网络结构、学习算法都随之发生改变．现在关于模糊前向神经网络的研究还较少，现有的一些文献，更多的停留在将二者进行简单地交叉，或是使用模糊数学的隶属函数作为前向神经网络的激励函数，或是使用前向神经网络强大数据处理功能来解决未知系统的规则确定问题，这些工作未将二者有效的整合在一起．随着我们处理问题难度的加大和非线性因素的不断增多，问题的描述和求解变得越来越困难，未知系统内部蕴含的函数关系几乎不可能得到，但借鉴于人类在处理问题时所具有的学习和模仿的天赋，许多智能算法孕育而生．神经网络因其能够描述大量数据之间的复杂函数关系，并具有分布式存储、并行性计算等特点，而备受关注．上世纪九十年代，模糊系统和神经网络结合起来后产生了模糊神经网络，它既是神经网络的模糊化，更是模糊系统的神经网络化，可以说它是某种意义下的折中处理，它既减小了神经网络的计算量，又增强了模糊系统的规则提取的便捷性．中山大学的张雨浓教授依据函数逼近理论，变换隐层神经元的激励函数，利用广义逆(伪逆)得到了隐层神经元最优权值直接确定算法，为研究高效高逼近精度的神经网络开辟了新的研究途径，奠定了扎实的理论和仿真实例基础[4-7]，但文[4～6]涉及的处理多输入系统的算法或是过于复杂，或是在实时性要求方面有待提高，或是没有较好的利用训练数据中一些可用数据．此外，文[8～11]利用多项式函数构造了不同的三层前向神经网络，但构造也较为复杂且逼近精度较低．鉴于神经网络强大的数据处理能力，关于它的研究层出不穷，促使了新的交叉方向的出现[12-14]．模糊系统中的隶属度函数为描述不确定性问题提供了定量化工具，本文将其与多输入单输出采样数据结合生成隐层神经元，充分考虑采样数据在建模中的重要性，同时为了还原原始数据，利用权值直接确定方法得到较高逼近精度的近似插值型神经网络．该神经网络逼近精度的高低将会在很大程度上取决于采样数据的多少．

1 双输入型模糊前向神经网络结构

为明确起见，下面先就一些基本术语和记号加以约定和标记．

对于三维Euclid空间，设 (x1,y1,z1), (x2,y2,z2),…, (xn,yn,zn)为双输入单输出采样数据，作为插值样本．

定义1设矩形区域V={(x,y)|a≤x≤b,c≤y≤d}， (x1,y1)，(x2,y2)，…，(xn,yn)是V内任意n个不同分点，已知Ai(x)∈C[a,b]，Bi(y)∈C[c,d]，且函数族{Ai(x)}，{Bi(y)}分别线性无关，则称{Ai(x)Bi(y)}为V上的乘积型基函数(i=1, 2,…,n)．

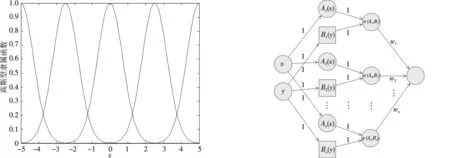
图1 高斯型隶属函数 图2 双输入型模糊前向神经网络拓扑结构Fig.1 Gauss type membership function Fig.2 Dual-input fuzzy feedforward neural network topology

依据定义3和前向神经网络的反馈机理构建四层前向神经网络，见图2．该拓扑结构中含双隐层．先是第一隐层利用高斯型隶属函数作为激励函数对双输入数据进行分离处理，后第二隐层借助乘积型基函数作为激励函数又将分离数据复合处理，这样做既重视了每组数据中不同分量的差异性，又重视每组数据中不同分量的相互联系．即

σ(Ai(x),Bi(y))=Ai(x)Bi(y)=exp[-(x-xi)2-(y-yi)2]，

简记为σ(Ai(x),Bi(y))=σi(x,y)，其中i=1, 2,…,n．第一、二隐层分别含2n与n个神经元．

为了简化计算，设定输入层神经元到第一隐层神经元连接权值和第一隐层神经元到第二隐层神经元连接权值全部为1，第二隐层神经元到输出层神经元连接权值向量为w=(w1,w2,…,wn)T，则与图2吻合的四层前向神经网络模型为

(1)

定理1依据公式(1)设计的四层前向神经网络是插值样本集{(xi,yi,zi) |zi=u(xi,yi),i=1, 2,…,n}的最佳平方逼近．

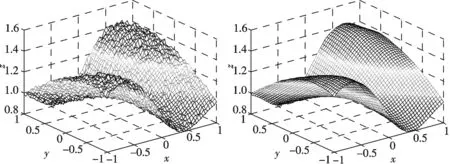
证第一隐层神经元激励函数选择为高斯型隶属函数，Ai(x)=exp[-(x-xi)2]，Bi(y)= exp[-(y-yi)2]，0

现先看函数族{A1(x),A2(x),…,An(x)}的线性相关性问题．设存在实数k1,k2,…,kn，使得k1A1(x)+k2A2(x)+…+knAn(x)=0，不妨取x=x1,…,x=xn，则有A1(x1)=A2(x2)=An(xn)=1，代入得矩阵方程为

显然Ai(xj)=Aj(xi)=exp[-(xi-xj)2]，故A=AT．

又由00，所以k1=k2=…=kn=0，即说明函数族{Ai(x)}线性无关且连续．

同理可证，函数族{Bi(y)}线性无关且连续，所以σ(Ai(x),Bi(y))=Ai(x)Bi(y)是V上的乘积型基函数．

由多元函数极值理论，利用插值样本集{(xi,yi,zi) |zi=u(xi,yi),i=1, 2,…,n}得到的神经网络模型实为插值型问题z=u(x,y)的解存在且唯一．故f为u在V上的最佳平方逼近函数．

2 双输入型模糊前向神经网络权值直接确定与算法实现

2.1 权值直接确定

采样数据蕴含着系统内部的输入与输出之间的函数关系，前面建立的双输入模糊前向神经网络，需要进一步使用训练数据进行训练，使其达到更高的逼近精度．一般而言，若训练数据个数为m，则m≫n．在本文建立的模糊前向神经网络过程中采用的插值样本集即是训练数据集的真子集．

定义4设实矩阵X∈Rn×m，如果U∈Rm×n，满足XUX=X，UXU=U，(XU)T=XU，(UX)T=UX，则称U为X的Moore-Penrose广义逆矩阵或伪逆．

依据张雨浓教授所提出的前向神经网络权值直接确定算法[4]，对于多输入单输出模糊前向神经网络，由误差反向传播学习算法亦得如下定理．

定理2依公式(1)建立的模糊前向神经网络在输入训练数据集为α=((x01,y01,z01)，(x02,y02,z02)，…，(x0m,y0m,z0m))，w=(w1,w2,(,wn)T是第二隐层与输出层神经元之间的连接权值向量，输入受激励矩阵U∈Rm×n，目标输出矩阵β= (z01,z02,(,z0m)T∈Rm，则模糊前向神经网络的最优权值可直接确定为

w=(UTU)-1UTβ.

(2)

证输入受激励矩阵

由矩阵论知识可知，对于矩阵方程组Uw=β，只有U是列满秩时，最小二乘解才是唯一的，且为(UTU)-1UT，否则便有无穷多个最小二乘解．其中σi(x0j,y0j)=Ai(x0j)Bi(y0j)>0,i=1,2,…,n,j=1, 2,…,m.

权值迭代公式为

w(k+1)=w(k)-ηUT[Uw(k)-β].

(3)

故对(3)两边求极限得最优权值向量w=w-ηUT[Uw-β]，即w=(UTU)-1UTβ，学习率η取为1．

定理3依据公式(1)设计的四层模糊前向神经网络是插值样本集{(xi,yi,zi) |zi=u(xi,yi),i=1, 2,…,n}的近似插值型神经网络．

由于w是对应权值向量方程组的最小二乘解，故满足z≈zi．

2.2 算法实现过程

为方便实现，对训练数据，以及由训练数据集中提取出的重要插值样本集进行重新排序．

步骤1由训练数据得到真实模型；

步骤2在训练数据中提取重要的插值样本集，对两组数据按照x和y的升序重新排序编号，由于插值样本集是训练数据集的真子集，所以必存在标号0i和j，使得xj=x0i,yj=y0i,zj=z0i,i=1,2,…,m;j=1, 2,…,n;

步骤3由插值样本集和训练数据集依据公式(1)、(2)，按照权值直接确定方法得到最优权值向量w，其中U的广义逆(伪逆)直接调用MATLAB中的pinv(U)得到；

步骤4由(1)确定逼近模型输出，最终由训练数据集的输入和逼近模型输出得逼近模型．

3 仿真实验

为验证算法的有效性，下面选择文[10]与[4]中出现的二元函数作为真实模型，给出逼近模型，并比较一些统计参数，如运行时间、相对误差、均方差等．需要指出的是本文实验的硬件电脑配置是Intel(R)Core(TM)i5-2450M CPU @2.5 GHZ,内存为4.00 G，64位操作系统．输入变量x∈[-1,1]，y∈[-1,1]，选择x和y的采样步长h=0.04,均匀采样获得训练数据集α含2601组数据．然后分别按照变量x和y的升序重新排列以便实现网络建模．对于两个目标函数，选择的插值样本集从α中获取，即相当于选择x和y的采样步长h1=kh，k=1,2,…，当然可以选择h1=h，但会增加计算的复杂度，在下面的实验中选择h1=0.08即可使得均方差、相对误差等指标达到预期目的．利用MATLAB7.5.0(R2007b)对目标函数1、2进行了建模，见图3～6，并对利用randn()函数对目标函数2加入了峰值为0.01的随机噪声，得到了去噪后的逼近模型，见图7～8．

目标函数1：z=4x2-2y2+8xy，

目标函数2：z=ysin(x+y)exp(-y2)+1.

图3 目标函数1与逼近模型Fig.3 The objective function of 1 and approximation model

图4 逼近模型绝对误差与相对误差Fig.4 Absolute error and relative error of approximation model

图5 目标函数2与逼近模型Fig.5 The objective function of 2 and approximation model

图6 逼近模型绝对误差与相对误差Fig.6 Absolute error and relative error of approximation model

图7 加噪目标函数2与去噪输出Fig.7 Noise target function 2 and de-noising output

图8 去噪绝对误差与相对误差Fig.8 De-noising of absolute and relative errors

从仿真实验的总体效果来讲，模糊前向神经网络在较短时间内完成了建模，较之文[10]，较好利用了训练数据集，逼近精度提高了至少5倍；较之文[4]，运行时间大幅度缩短，均方差和相对误差等指标只是有些稍逊，但在采样误差和设备精度的硬件设施的制约下，提高反应时间显得更为重要；在目标函数加入噪声后，本文方法依然有效，说明它可以有效去除测量误差等干扰因素的影响，具体参数指标见表1．

表1 网络性能

4 结束语

直接来源于训练数据集的插值样本集，为建立模模糊前向神经网络隐层神经元提供了重要的数据．根据实际需要和采样数据的多少，灵活调节隐层神经元个数，在确定神经元个数后利用权值直接确定方法确定最优权值，使得网络结构达到较好的设置．数值仿真实验表明，双输入型模糊前向神经网络可以解决复杂数据集的实时性高精度建模问题．

参考文献：

[1] 黄媛玉,毛 弋. 基于主成分分析法的遗传神经网络模型对电力系统的短期负荷预测[J]. 湖南师范大学自然科学学报, 2011,34(5):26-31.

[2] 周春光,张 冰,梁艳春，等. 模糊神经网络及其在时间序列分析中的应用[J]. 软件学报, 1999,10(12):1304-1309.

[3] 沈 谦,王 涛,张德龙. 基于模糊前向神经网络的PVC识别方法[J]. 计算机工程与科学, 2000,22(6):60-62.

[4] 张雨浓，劳稳超，余晓填,等. 两输入幂激励前向神经网络权值与结构确定[J].计算机工程与应用, 2012,48(15):102-106.

[5] 张雨浓,曲 璐,陈俊维,等. 多输入Sigmoid激励函数神经网络权值与结构确定法[J]. 计算机应用研究, 2012,29(11):4113-4151.

[6] 肖秀春,张雨浓,姜孝华. MISO多元广义多项式神经网络及其权值直接求解[J]. 中山大学学报：自然科学版, 2009,48(4):42-56.

[7] 张雨浓,杨逸文. PID神经元网络之权值直接确定法研究[J]. 计算机工程与应用, 2009,45(19):189-191.

[8] 曹飞龙,徐宗本,梁吉业. 多项式函数的神经网络逼近：网络的构造与逼近算法[J]. 计算机学报, 2003,26(8):906-912.

[9] 王建军,徐宗本. 多元多项式函数的三层前向神经网络逼近方法[J]. 计算机学报, 2009,32(12):2482-2488.

[10] 曹飞龙,张永全,潘 星. 构造前向神经网络逼近多项式函数[J]. 模式识别与人工智能, 2007,20(3):331-335.

[11] 曹飞龙,徐宗本. 多变元周期函数的神经网络逼近：逼近阶估计[J]. 计算机学报, 2001,24(9):903-908.

[12] 邹阿金,张雨浓,肖秀春. Hermite混沌神经网络异步加密算法[J]. 智能系统学报, 2009,4(5):458-462.

[13] ZHANG Y N, WANG J. Recurrent neural networks for nonlinear output regulation[J]. Automatica, 2001,37(8):1161-1173.

[14] 杨文光. 权值直接确定的三角型模糊前向神经网络[J]. 中山大学学报:自然科学版,2013,52(2):33-37.