三电平感应电机模型预测直接电流控制策略*

吴轩钦，曹晓冬，王从刚

(中国矿业大学信息与电气工程学院，江苏徐州 221008)

0 引言

在中压兆瓦级大功率电气传动场合中，多使用多电平拓扑结构变流器以达到减少开关器件动作次数，降低开关频率以及输出更大的调制电压[1-3]。为了提高电机调速系统电流跟踪性能，提出滞环电流控制和预测电流控制等。滞环电流控制由于其结构简单、方便实现获得广泛应用。随着高性能数字处理器(DSP)和现场可编程门阵列(FPGA)的迅速发展，以预测控制技术为代表的现代控制技术才成功应用于电力电子与电机调速领域。

模型预测控制(Model Predictive Control，MPC)从工业过程控制发展而来，并且已经应用于先进制造、航空航天、环境等众多领域[4-5]。当采用模型预测直接电流控制技术(Model Predictive Direct Current Control，MPDCC)[6-7]进行电机调速系统内环控制时，系统无需使用PWM技术，变流器开关状态根据系统预测值，结合目标方程在线寻优后，即可直接输出。与传统控制策略相比，MPDCC系统具有响应迅速、结构清晰、在线寻优更加智能等优势。

本文分析了三电平感应电机调速系统离散数学模型，给出了MPDCC中的目标函数和滚动寻优设计方法，进行了试验分析。

1 系统数学模型

三电平异步电机调速系统结构图如图1所示，其中，Udc为直流母线电压;C1、C2为母线滤波电容;Sa，Sb，Sc为变流器abc三相输出对应开关状态，由于系统采用三电平拓扑结构，即Sa，Sb，Sc∈[－1，0，1]，变流器包含 33=27 种开关状态。

图1 三电平感应电机调速系统结构框图

在两相静止αβ坐标下，感应电机定子电流、转子磁链和定子电压关系数学表达式为

其中:isα、isβ——定子电流 α、β 轴分量;

ω——转子角频率;

ψrα、ψrβ——转子磁链 α、β 轴分量;

Ls——定子自感;

Lr、Rs——转子自感、转子电阻;

Lm——互感;

Tr——转子电磁时间常数，Tr=Lr/Rr;

三电平中点电位与变流器三相开关状态和各相电流的关系可表示为

式中:uo——三电平拓扑中点电位;

Cdc——上下母线电容值;

ua、ub、uc——变流器 ABC 三相输出相电压;ia、ib、ic——ABC 三相对应电流。

2 MPDCC控制原理

MPDCC系统控制框图如图2所示，系统由轨迹预测、模型预测、目标方程建立、全阶磁链观测器四个部分组成。

图2 三电平感应电机系统控制框图

2.1 轨迹预测

MPDCC系统中有两个PI调节器，分别是转矩PI调节器和励磁电流PI调节器，其作用为实现转速及磁通跟踪给定。经PI调节器调节后系统获得所需转矩电流和励磁电流，经坐标变换后即可求得静止αβ坐标系下电流给定值

在实际系统中，为消除数字控制系统中电流给定与实际电流控制偏差，需对给定信号进行轨迹预测，采用二阶外推法即可直接求得k+1时刻电子电流预测值

2.2 模型预测

假设实际数字处理系统采样周期Ts足够小，式(1)、式(2)中的微分项可近似为

式中:i(k)——系统本次采样定子电流值;

i(k－1)——系统前一采样定子电流值。将式(5)代入式(1)、式(2)求得

采用式(6)、式(7)即可在第k次采样时刻预测系统第k+1次性能表现(电流值)。同理对式(3)离散化，可得中点电位预测表达式

2.3 目标方程建立

MPC策略根据系统控制目标建立目标方程，结合滚动优化，在线选取使控制目标最优的系统输入，所以目标方程的优劣直接影响到整个MPC系统的性能。

三电平MPDCC控制器主要包括跟踪外环电流给定和控制中点电位平衡。通过在线滚动优化，使两个控制目标最优的开关状态将作为最优开关状态输出，通过建立目标方程J对其进行数学描述为

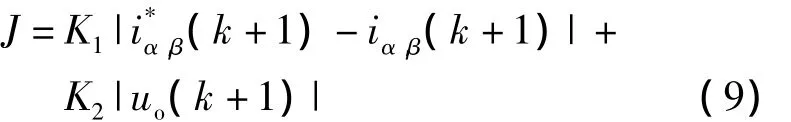
式中:K1、K2——系统加权系数，确定对应控制目标在整个目标函数J中所占权重比例;

i*(k+1)——系统第k+1时刻外环电流给定值。

系统每次采样后，将三电平拓扑包含的27种开关状态代入目标函数J中，经过在线滚动优化后，使J取值最小的开关状态即为系统最优开关状态。

2.4 全阶磁链观测器

采用一种全阶闭环磁链观测器[8]获得准确的磁链观测值和转子磁链定向角，其原理框图如图3所示，由开环电流模型及自适应电压模型组成。其中开环电流模型作为隐含的给定，在低速段可提供比较准确的值。自适应电压模型具有较宽的调速范围，通过合理选择闭环特征值可以很好地实现两者的平滑切换，即在宽速度范围内提供准确的定向角和磁链观测值。

图3 全阶闭环磁链观测器

3 试验

为了验证感应电机MPDCC策略的可行性，基于DSP(TMS320F2812)+FPGA处理器搭建三电平感应电机调速系统试验平台。DSP作为主控器件，完成MPDCC核心控制算法，FPGA作为辅助控制器件，完成AD采样、DA输出、脉冲死区等辅助功能。试验所用样机主要参数如表1所示。

表1 试验样机参数表

图4(a)、图4(b)为电机控制运行时，转速给定值n*突变时电机实际转速n、电磁转矩Te、a 相电流 ia、转子磁链 ψrα、ψrβ和定向角 θ试验波形。由图可知，动态突变时电机转矩响应迅速，转速快速跟踪给定且稳态无静差;转子磁链ψrα、ψrβ在动稳态全过程中波形正弦度高，定向角平滑。

图4(c)为电机空载时a相电流ia和线电压uab波形，此时电机转速n=500 r/min。由图可知，稳态电流波形正弦度高，线电压分布均匀，开关频率较低。图4(d)为突加负载时，n、ia和Te波形，可见电机转矩响应迅速，实际转速经过很短的跌落后可跟踪上给定转速。

图4 试验结果

4 结语

对一种新颖的三电平逆变器驱动的感应电机MPDCC控制策略进行了研究。采用在线优化寻求最优开关矢量，相比传统矢量控制技术具有无需调制模块、算法控制灵活、动态响应迅速等特点，但其也相应存在在线计算量大、开关频率不固定等弊端。MPDCC策略为中压大功率三电平感应电机高性能调速系统设计提供了一套新颖的控制方案。

[1]RODRIGUEZ J，BERNET S，PETER K，et al.A survey on neutral-point-clamped inverters[J].IEEE Transactions on Industrial Electronics，2010，57(7):2219-2230.

[2]NABAE A，TAKAHASHI I，AKAGI H，et al.A new neutral point clamped PWM inverter[J].IEEE Transations on Industrial Application，1981，12(5):518-523.

[3]赵辉，李瑞，王红君，等.60°坐标系下三电平逆变器SVPWM方法的研究[J].中国电机工程学报，2008，28(24):39-45.

[4]席裕庚，李德伟，林姝.模型预测控制—现状与挑战[J].自动化学报，2012，38(9):222-236.

[5]席裕庚，李德伟.预测控制定性综合理论的基本思路和研究现状[J].自动化学报，2008，34(10):1225-1234.

[6]CORTES P，KAZMIERKOWSKIM P，KENNEL R M，et al.Predictive control in power electronics and drives[J].IEEE Transactions on Industrial Electronics，2008，55(12):4312-4324.

[7]CORTES P，RODRIGUEZJ，SILVAC.Delay compensation in model predictive current control of a three-phase inverter[J].IEEE Transactions on Industrial Electronics，2012，59(2):1323-1325.

[8]LASCU C，BOLDEA I，BLAABJERG F.A modified direct torque control for induction motor sensorless drive[J].IEEE Transactions on Industrial Applications，2000，36(1):122-130.