火箭炮调炮精度的几种测量方法比较研究
方安国,徐 锐,张金萍
(湖北江山重工有限责任公司,湖北 襄阳 441057)
随着电子技术、计算机技术和定位定向技术的发展,火箭炮传统的间接瞄准己逐步被自动操瞄所代替。间接瞄准方式是将射击诸元装定好后,调炮对准间接目标即可,其精度保证是在出厂前调试中对瞄准具和瞄准镜进行零位校准的程度,而自动操瞄要校准的环节相对较多,如倾斜传感器、定位定向仪的安装,倾斜修正的计算精度,弹性变形修正等都将影响调炮精度[1],在装配调试中对上述多个环节进行调整,以便满足调炮精度的要求。自动操瞄调炮精度是武器系统最重要的战技指标之一,因此要对调炮精度进行测量。下面给出几种测量调炮精度的方法。
1 双经纬仪瞄准具测量方法
在炮管的上方由前到尾拉1根细线,且与炮管同轴,双经纬仪[2-3]瞄准具测量方法如图1所示。

设AA1是与炮管同轴的细线,C为AA1延长线上的一点,将一台经纬仪放置于点C,自动操瞄调炮到位后AA1旋转至BB1,C1为BB1延长线上的一点,将另一台经纬仪放置于点C1,此时测得角度α和β,即可求出θ,θ即为实测的方向调炮角。
θ=180°-α-β
(1)
高低角可直接从瞄准具上读取。
将测得方向角和高低角减去射击诸元,就是误差,根据误差可求出调炮精度。
此测量方法原理简单,易学易懂,但操作上必须将炮管调一定的角度,便于测量,且经纬仪要准确地放在拉线的延长线上,因此操作比较麻烦。
由于经纬仪精度较高,误差主要在测量上,操作精度将是方向测量误差的主要来源。高低精度主要是瞄准具的精度,其精度为1密位。
2 瞄准镜经纬仪瞄准具测量方法
瞄准镜经纬仪[4]瞄准具测量方法如图2所示。

瞄准镜作为配属在火箭炮上的设备,供火箭炮进行瞄准和标定。主要由镜头和镜体组成,行军时放入工具箱,使用时装入瞄准具内,通过紧定螺钉实现方向定位与固定,防止因振动冲击产生的各种误差。
设AA1是瞄准镜纵轴线,与基准管轴线在水平面投影平行,A点为调炮前瞄准镜的位置,B点为调炮后瞄准镜的位置,此时BB1是瞄准镜纵轴线,与基准管轴线在水平面投影平行,经纬仪放置在炮车左侧或后侧一点C上。根据图2,θ角即为实测的方向调炮角。计算如下式:
θ=α2-α1-β
(2)
当经纬仪足够远时,即变成远处的标杆。实际操作中,标杆放置在距炮车1 km处,此时的β值很小,可以忽略不计。
高低角可直接从瞄准具上读取。
将测得方向角和高低角减去射击诸元,就是误差,根据误差可求出调炮精度。
调炮精度分析计算如下式:
(3)

高低精度主要是瞄准具的精度,其精度为1密位。
采用这种方法进行测量,操作方便,简单易行,但由于瞄准镜、瞄准具精度在1密位左右,因此这种方法可以用在自动操瞄精度要求不太高的场合。
3 双经纬仪测量方法
3.1 方向操瞄精度测量方法
选定一根便于测量的炮管,在炮管的前后两端贴十字线,十字线的连线应与炮管轴线平行,如图3所示,点D和C为十字点在水平面上的投影,经纬仪分别放置于点A和B,根据图3可求取θ角,即为操瞄调炮方向角的测量值。
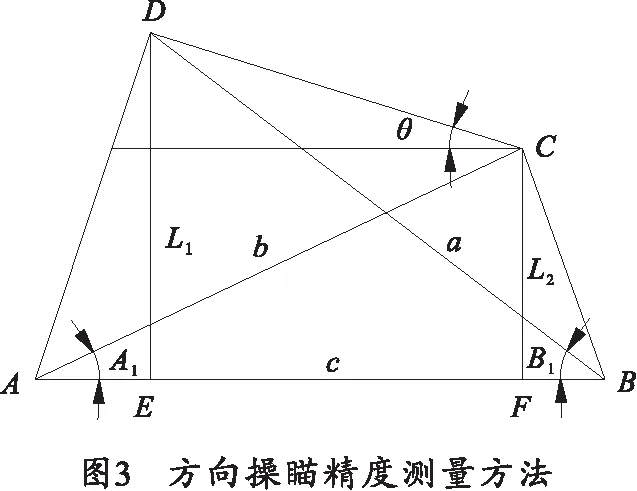
求解过程如下:
(4)
根据上式求出θ,与设定值相减就可以得出方向调炮精度。
3.2 高低操瞄精度测量方法
如图4所示,设H点和G点为炮管上前后两十字点,D点和C点是其在水平面上的投影,可求取β角,即为操瞄调炮高低角的测量值。

求解过程如下:
(5)
根据上式求出β,与设定值相减就可以得出高低调炮精度。
4 3种测量方法分析比较
通过对工作实践中常用的3种调炮精度测量方法进行分析,建立了相应的数学模型,推导出了相应的计算公式。对某火箭炮在实际高低角920密位、实际方向角287.17密位时的7次调炮数据见表1。
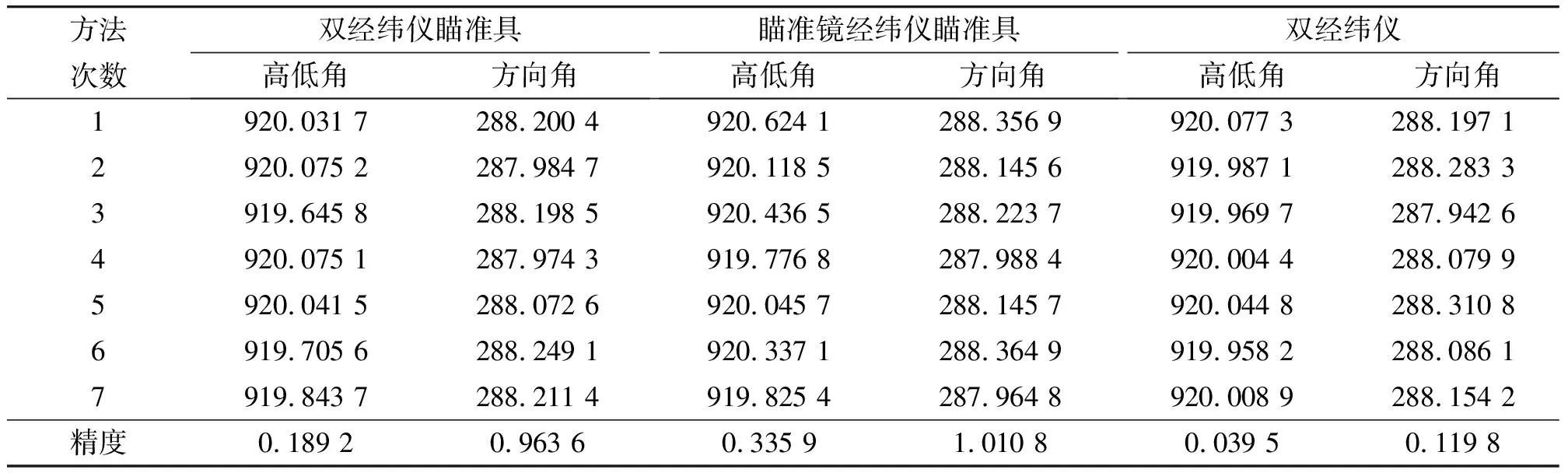
表1 实际调炮计算值 密位
对上述3种调炮精度测量方法的分析比较结果见表2。

表2 3种测量方法分析比较
5 结束语
在长期工作实践的基础上,笔者对3种调炮精度测量方法[5]进行了总结,并对调炮过程可能产生误差的来源等进行了分析。通过分析可知,相对于其他两种测量方法,双经纬仪测量方法在实际测量中操作简单、方便,且精度也较高,在三种测量方法中应作为首选。
参考文献(References)
[1] 罗鸿飞, 张英堂, 任国全, 等. 基于空间坐标解算的火炮调炮精度检测方法研究[J]. 火炮发射与控制学报, 2007(3): 50-52.
LUO Hong-fei, ZHANG Ying-tang, REN Guo-quan, et al. Research on measuring method of gun rotated accuracy based on spatial coordinate algorithm[J]. Journal of Gun Launch & Control, 2007(3): 50-52. (in Chinese)
[2] 孙泽林, 王昭, 翟唤春. 双经纬仪交会测量火炮调炮精度的误差分析与抑制[J]. 光学精密工程, 2010, 19(10): 2434-2441.
SUN Ze-lin, WANG Zhao, ZHAI Huan-chun. Analysis and control of error on two theodolite intersection measurement for gun raotaed accuracy of artillery[J]. Optics and Precision Engineering, 2010, 19(10):2434-2441. (in Chinese)
[3] 张滋黎, 邾继贵, 耿娜, 等. 双经纬仪三维坐标测量系统设计[J]. 传感技术学报, 2010, 23(5): 60-64.
ZHANG Zi-li,ZHU Ji-gui, GENG Na, et al. The design of double theodolite 3D coordinate measurement system[J]. Chinese Journal of Sensors and Actuators, 2010, 23(5): 60-64. (in Chinese)
[4] 董起顺, 姜涛, 苏成志. 火炮复瞄精度测试中经纬仪的最佳布站研究[J]. 兵工学报, 2007, 28(5): 13-15.
DONG Qi-shun, JIANG Tao, SU Cheng-zhi. Theodolite optimal disposition in artillery duplicate-aim precision detection[J]. Acta Armamentarii, 2007, 28(5): 13-15. (in Chinese)
[5] 曾刊, 赖文娟. 双经纬仪调炮精度检测系统[J]. 兵工自动化, 2011 (7): 73-75.
ZENG Kan, LAI Wen-juan. Gun slaving precision detecting system of double-theodolite[J]. Ordnance Industry Automation, 2011 (7): 73-75. (in Chinese)

