混杂纤维高性能混凝土深梁的剪切延性

刘胜兵，徐礼华

（1.武汉工程大学 环境与城市建设学院，武汉 430074；2.武汉大学 土木建筑工程学院，武汉 430072）

延性是指材料、构件或结构在各种作用下进入非线性状态后，在承载力不显著降低情况下的变形能力。延性可分为材料延性、截面延性、构件延性和结构延性。对于混凝土构件的破坏，除了应满足强度、刚度、稳定性等方面的要求外，还要求具有良好的延性，使结构具有充分的变形能力和良好的动力性能，防止结构在使用过程中发生脆性破坏。钢筋混凝土深梁具有刚度大、受力特性合理、承载力大等特点，在高层建筑和大跨结构等实际工程中得到广泛应用［1］。深梁构件由于所受弯矩较小，剪力很大，极易发生剪切破坏，而剪切破坏属于脆性破坏，破坏后果极为严重，因此对深梁剪切破坏下的延性进行研究是非常必要的。目前，中国外对混凝土受弯构件的延性十分重视，这方面的研究成果较多。文献［2］对混杂纤维高性能混凝土深梁正截面受弯性能进行了研究，指出混杂纤维可以显著改善高性能混凝土深梁的正截面延性，但文中未对延性进行定量分析。Xie等［3－4］仿照正截面延性研究方法，定义了剪切延性指标，对梁的剪切延性进行了定量分析。对于深梁的受剪性能，虽然研究成果较多，但内容多限于受剪承载力和计算模型等方面［5－10］。对于深梁剪切延性的研究，Rao等［11－12］研究了尺寸变化对混凝土深梁的剪切延性影响。有关混杂纤维高性能混凝土深梁剪切延性的研究，目前还未见诸报道，笔者对混杂纤维高性能混凝土深梁剪切破坏下的变形和延性进行定量分析和研究，为《纤维混凝土结构技术规程》（CECS 38：2004）［13］增补有关混杂纤维混凝土深梁的内容提供参考。

1 试验概况

1.1 试件设计

按照《纤维混凝土结构技术规程》（CECS 38：2004）的有关要求，通过“正交设计法”［14］，采用 L18（21×37）正交表设计了18组混杂纤维高性能混凝土深梁。考虑的影响因素有6个：钢纤维体积率、钢纤维长径比、钢纤维外形、聚丙烯纤维体积率、水平分布钢筋配筋率及竖向分布钢筋配筋率。

各因素的水平数分别安排如下：1）钢纤维体积率分别取0.5%、1.0%、1.5%共3个水平；2）钢纤维外形采用端钩形和波纹形2个水平；3）钢纤维长径比分别取30、50、70共3个水平；4）聚丙烯纤维体积率分别取0.055%、0.11%、0.165%共3个水平；5）水平分布钢筋配筋率分别取0、0.581%、0.872%共3个水平；6）竖向分布钢筋配筋率分别取0、0.581%、0.872%共3个水平。

为便于对比，还设计了2组不加纤维的普通高性能混凝土深梁。20组深梁剪跨比均为1，跨高比均为1.6。为保证深梁发生剪切破坏，深梁下部的0.2h（h为梁高）范围内均配置了418作为纵向受力钢筋，分上下2层布置，配筋率为1.356%。水平及竖向分布钢筋采用光圆钢筋，配筋率为0.872%时腹筋的布置为2φ10＠120，配筋率为0.581%时腹筋的布置为2φ10＠190。深梁截面尺寸均为150mm×500mm，长1040mm，净跨800mm。试件具体参数及试验结果见表1所示。

表1 试件参数及试验结果

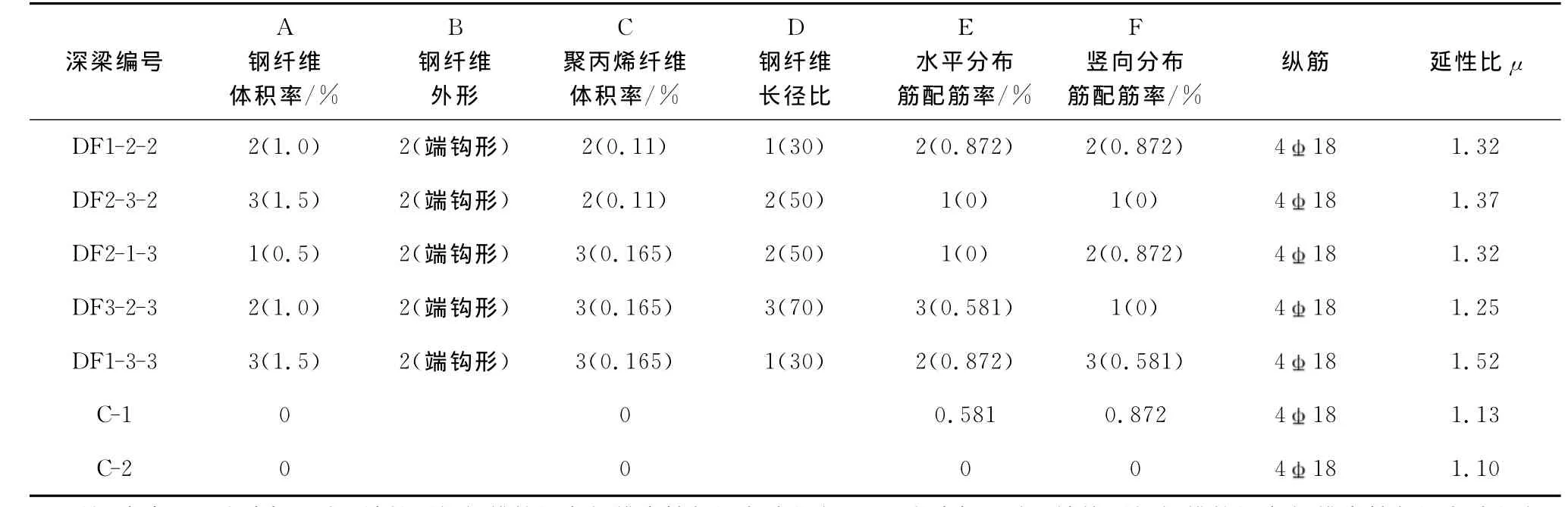
续表1

1.2 试验加载装置

试验在5000kN压力试验机上进行，取用2000kN量程。试验深梁为简支梁，采用跨中单点集中加载，试验加载装置见图1、图2。

图1 试验加载装置示意图（单位mm）

图2 5000kN压力试验机加载装置

2 剪切延性试验结果及分析

2.1 剪切延性评定指标

为评定混杂纤维HPC深梁剪切破坏下的延性，可以分别比较其延性比μ（也称延性系数）。延性比定义为，荷载 跨中挠度曲线的下降段上对应85%Pmax的挠度Du与初始屈服点所对应的挠度Dy之比，计算公式为μ＝Du／Dy。屈服变形Dy的取值标准，至今尚无统一方法。一般情况下，Dy是受拉钢筋开始屈服时相应荷载下的变形，此值对应于变形曲线上的拐点。但由于钢筋混凝土受剪构件的特殊性，变形曲线没有明显的拐点，转折点往往在一较小区段内。确定Dy一般采用以下2种方法：1）能量法（图3），用折线OYU代替原来的荷载位移曲线，使曲线下的总面积相等，即图中面积OAB＝面积YUB；2）几何作图法（图4），作直线与曲线初始段相切，与过U的水平线交于点A，作垂线AB交曲线于B，连结OB并延伸于水平线交于C点，过点C作OD 的垂线与曲线交于Y［15］。参考文献［16］采用能量法确定初始屈服点，统一取荷载位移曲线上升段0.85 Pmax对应的点为初始屈服点。

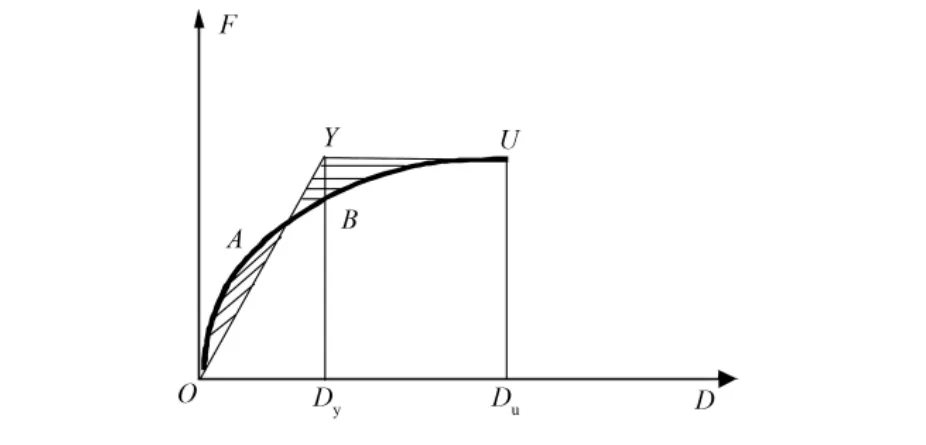
图3 能量法确定初始屈服点

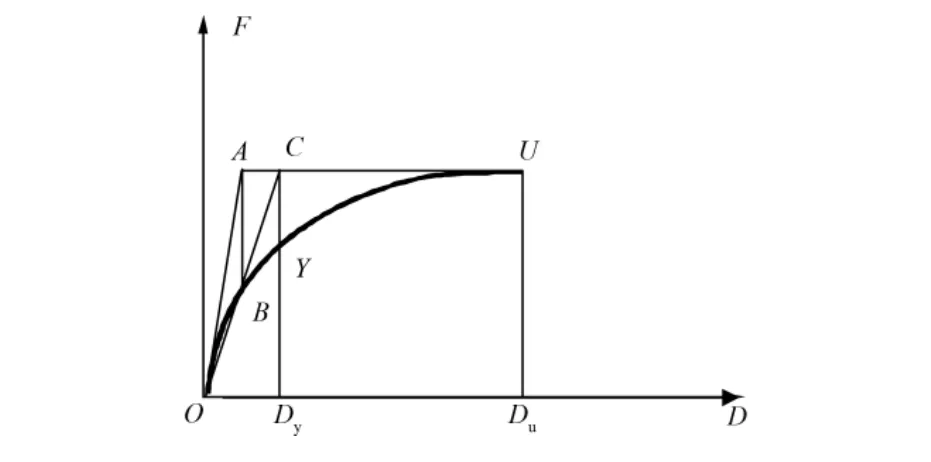
图4 几何作图法确定初始屈服点

2.2 剪切延性试验结果

根据试验结果，按照上述定义计算试验深梁的延性比见表1。

2.3 剪切延性分析

2.3.1 因素的影响大小比较 延性比计算结果的直观分析见表2。折算极差反应了不同因素的影响大小，可以看出，对于深梁剪切破坏时的延性，各因素的影响大小依次为：A（钢纤维体积率）＞D（钢纤维长径比）＞C（聚丙烯纤维体积率）＞F（竖向分布钢筋配筋率）＞E（水平分布钢筋配筋率）＞B（钢纤维外形）。

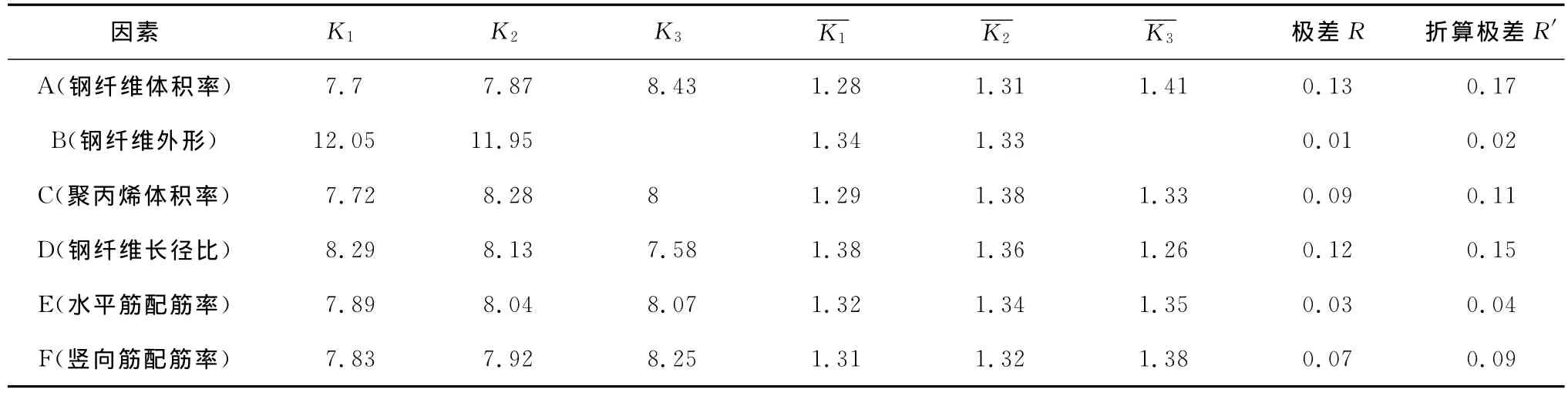
表2 延性比直观分析计算表

2.3.2 混杂纤维的影响 从表1可以得出，无腹筋深梁 BF1－2－1及 DF2－3－2与对比梁 C－2相比，延性比分别提高了15%和24.5%；有腹筋深梁BF1－3－2及BF2－2－3与对比梁C－1相比，延性比分别提高了40.7%和14.2%。表明混杂纤维可显著提高深梁的延性，但延性比仍达不到延性破坏的要求，不足以从破坏形态上根本改变深梁剪切破坏时的脆性。

混杂纤维对受剪破坏深梁延性的增强可以从以下几个方面来解释：1）混杂纤维提高了混凝土的韧性及剪压区混凝土的极限压应变和变形能力，对高强高性能混凝土的抗压强度也有所提高；2）当深梁斜截面开裂时，由于“桥架”于斜裂缝的钢纤维和聚丙烯纤维具有类似箍筋的“微筋材”作用，混杂纤维在不同层次和阶段承担了混凝土释放的应力，同时也抑制了斜裂缝的发展，斜裂缝张开的过程同时也是聚丙烯纤维和钢纤维在不同阶段缓慢拔出的过程，一定程度上缓解了破坏的突发性，使深梁达极限承载力后荷载不会快速回落；3）混杂纤维增强了混凝土中钢筋与骨料的握裹力和粘结力，提高了纵向受拉钢筋的销栓作用和水平及竖向分布钢筋对混凝土的约束。

2.3.3 钢纤维体积率的影响 钢纤维体积率对深梁剪切破坏时延性比的影响见图5。随着钢纤维掺量的增大，深梁的延性比有所提高。当钢纤维体积率从0.5%增大到1.5%时，深梁延性比提高了10.2%。

2.3.4 钢纤维外形的影响 图6给出了钢纤维外形对深梁剪切破坏延性比的影响。从图中看出波纹形钢纤维的增强效果稍好于端钩形钢纤维，但差别非常小。另外，由于试验试件个数较少，且深梁的剪切破坏离散性较大，因此，关于这方面的探讨，可以进一步进行研究。

图5 钢纤维体积率对延性比的影响

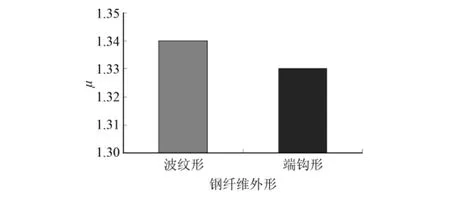
图6 钢纤维外形对延性比的影响

2.3.5 钢纤维长径比的影响 图7给出了钢纤维长径比对深梁剪切破坏时延性比的影响。从图中可以看出，钢纤维长径比从30增加到70时，深梁的延性比逐渐减小，减小了8.7%，钢纤维长径比为30时混杂纤维高性能混凝土深梁剪切破坏延性最好。

2.3.6 聚丙烯纤维体积率的影响 图8给出了聚丙烯纤维体积率对深梁剪切延性比的影响。从图中可以看出，当聚丙烯纤维体积率从0.055%增加到0.165%时，深梁剪切破坏的延性比先增加后减小。聚丙烯纤维体积率为0.11%时混杂纤维高性能混凝土深梁剪切延性最好。

图7 钢纤维长径比对延性比的影响

图8 聚丙烯纤维体积率对延性比的影响

2.3.7 水平分布钢筋配筋率的影响 水平分布钢筋配筋率对深梁剪切破坏延性比的影响见图9。从图中可以看出，当水平分布钢筋配筋率从0增加到0.581%时，深梁剪切破坏延性比增加了2.3%，而当配筋率从0.581%增加到0.872%时，延性比反而降低了0.74%。表明一定数量的水平分布钢筋对提高深梁剪切延性是有利的，但配筋率过大则会对延性产生不利影响，由于试验数据差别不大，也不排除试验误差所致。

图9 水平分布钢筋配筋率对延性比的影响

2.3.8 竖向分布钢筋配筋率的影响 图10给出了竖向分布钢筋配筋率对深梁剪切延性比的影响趋势图。从图中可以看出，当竖向分布钢筋配筋率从0增加到0.581%时，深梁剪切破坏的延性比增加了5.3%，而当配筋率从0.581%增加到0.872%时，延性比反而降低了4.3%。表明一定数量的竖向分布钢筋对提高深梁延性是有利的，但配筋率过大则会对延性产生不利影响，与普通混凝土深梁一致。

图10 竖向分布钢筋配筋率对延性比的影响

3 有限元模拟分析

为验证试验结果的有效性，通过选取合理的材料本构模型、破坏准则以及单元类型，采用有限元分析软件ABAQUS对20组深梁受剪破坏过程进行非线性有限元分析，并将有限元计算结果与试验结果进行对比。

3.1 钢筋的本构模型

钢筋采用有限元软件ABAQUS中的塑性分析模型，该模型在多轴应力状态下满足经典的Von Mises屈服准则，采用各向同性的强化准则，并服从相关流动法则。钢筋选择四折线的本构模型如图11所示，与钢材塑性性能有关的参数可由钢材的单轴拉伸应力 应变关系曲线确定，四折线模型的数学表达式如下：

图11 钢筋应力 应变曲线

3.2 混杂纤维高性能混凝土的本构模型

混杂纤维高性能混凝土是由钢筋、混凝土及2种或2种以上纤维等多种不同物理性能的材料复合而成，其本构关系比普通混凝土更为复杂。笔者采用ABAQUS提供的混凝土损伤塑性模型，由于目前还没有混杂纤维高性能混凝土的本构模型，采用文献［17］钢纤维混凝土的单轴本构模型，通过修正其初始弹性模量来求得各种混杂组合下纤维混凝土的本构曲线。混杂纤维高性能混凝土单轴拉伸曲线参考文献［18］，损伤因子采用文献［19］中的公式计算。

3.3 有限元模型的建立

钢筋采用二节点线性桁架单元T3D2模拟，混杂纤维混凝土采用C3D8R单元，此单元为八节点减缩积分实体单元，可以减少模拟计算所需时间，得到较好的位移和应力结果，同时又适用于采用了接触（Contact）的模型分析。由于混杂纤维强化了钢筋与混凝土之间的销栓作用，且深梁开裂后斜裂缝宽度较小，因此不考虑钢筋与混杂纤维混凝土之间的滑移。由于深梁受剪承载力较大，为避免出现局压破坏造成计算不收敛，支座及加载板均由离散刚体（Discrete Rigid）模拟，其与混杂纤维HPC深梁之间的接触采用接触单元（Contact），接触属性中切向方向采用罚函数（Penalty）定义，摩擦系数取为0.25，法向方向采用硬接触（Hard Contact）。如果采用力加载，往往会因为荷载变化不敏感而导致收敛困难，而采用位移加载会比较容易得到荷载 跨中挠度曲线的下降段，因此采用位移加载，在加载板上沿z向施加位移荷载，根据试验所得到的荷载 跨中挠度曲线每一级荷载对应的挠度值来施加位移荷载。

3.4 有限元计算结果及分析

3.4.1 深梁破坏形态 图12为深梁 BF1－3－2的最大主塑性应变云图，从中可以清楚地看出开裂位置及破坏形态，从图13可以看出试验得到的裂缝分布图及破坏形态。可见，有限元模拟结果与试验结果吻合良好。

图12 深梁BF1－3－2数值模拟破坏形态

图13 深梁BF1－3－2试验破坏形态

3.4.2 荷载 跨中挠度曲线 荷载 跨中挠度有限元模拟曲线与试验曲线对比见图14。可以看到，有限元模拟曲线与试验曲线总体较为吻合。不同之处是，有限元模拟曲线上升段出现明显的拐点，而试验曲线上升阶段并没有拐点。其原因是深梁在受剪试验过程中，随着荷载的增加，其跨中挠度逐渐增大，深梁的临界斜裂缝一旦出现便迅速发展，临界斜裂缝处混凝土因开裂退出工作。由于混凝土开裂处的钢纤维和聚丙烯纤维还未来得及充分发挥作用，其承载力并不增长甚至有所下降，所以在曲线图上表现为类似一屈服平台。而在深梁受剪试验过程中，由于深梁开始受荷阶段由力加载控制，很难测出曲线这一拐点。

图14 荷载 跨中挠度模拟曲线与试验曲线对比

3.4.3 混凝土应力分布 由于试验测量的局限性，不可能通过应变片测得深梁所有位置的应力应变分布情况，而有限元模拟则能够很好地弥补这一缺陷，可以方便地获取深梁混凝土上任意位置的应力应变分布情况。深梁BF1－3－2混凝土的最大主应力分布云图见图15，由于深梁发生劈裂破坏，最大主应力法线方向即为混凝土开裂方向，可以看出，混凝土开裂发生于集中力加载点与支座连线方向，与试验结果吻合。

图15 深梁BF1－3－2混凝土的最大主应力分布云图

3.4.4 有限元模拟与试验结果比较 根据有限元后处理计算结果及前述剪切延性计算方法，得出每组深梁延性比的数值模拟结果，模拟值与试验值对比见表3。有限元模拟值与试验值的比值在0.89～1.15之间，可见符合较好。

表3 模拟值与试验值对比

续表3

4 结 论

1）对于混杂纤维高性能混凝土深梁剪切延性，各因素的影响顺序依次为：A（钢纤维体积率）＞D（钢纤维长径比）＞C（聚丙烯纤维体积率）＞F（竖向分布钢筋配筋率）＞E（水平分布钢筋配筋率）＞B（钢纤维外形）。

2）混杂纤维能显著提高高性能混凝土深梁剪切延性，无腹筋深梁延性比可提高15%～24.5%，有腹筋深梁延性比可提高14.2%～40.7%，但仍达不到延性破坏的要求，不足以从破坏形态上根本改变深梁剪切破坏时的脆性。

3）当钢纤维体积率在0.5%～1.5%之间时，深梁剪切延性随着钢纤维体积率的增大而提高；聚丙烯纤维体积率为0.11%时混杂纤维高性能混凝土深梁的剪切延性最好。

4）一定数量的水平分布钢筋和竖向分布钢筋对提高深梁延性是有利的，但配筋率过大会对延性产生不利影响。

5）有限元模拟结果与试验结果符合较好，且有限元模拟能反映出混杂纤维HPC深梁荷载 跨中挠度试验曲线上无法测出的拐点。

［1］丁大钧.高性能混凝土及其在工程中的应用［M］.北京：机械工业出版社，2007.

［2］夏冬桃.混杂纤维增强高性能混凝土深梁抗弯性能试验研究［D］.武汉：武汉大学，2007.

［3］Xie Y L，Ahmad S H.Shear ductility of reinforced concrete beams of normal and high strength concrete［J］.ACI Structural Journal，1994，91（2）：140－149.

［4］Ahmad S H，Xie Y L.Shear ductility of reinforced lightweight concrete beams of normal strength and high strength concrete ［J］. Cement and Concrete Composites，1995，17：147－159.

［5］Patel V R，Rana A，Pandya I I.Shear strength of polypropylene fiber reinforced concrete moderate deep beams without stirrups ［J］.Journal of Structural Engineering，2011，37（5）：364－368.

［6］Kim B H，Yun Y M.An indeterminate strut－tie model and load distribution ratio for RC deep beams－（I）model＆load distribution ratio［J］.Advances in Structural Engineering，2011，14（6）：1031－1041.

［7］Lee H K，Cheong S H，Ha S K.Behavior and performance of RC T－section deep beams externally strengthened in shear with CFRP sheets ［J］.Composite Structures，2011，93（2）：911－922.

［8］Lee H K，Cheong S H，Ha S K.Shear behavior and performance of deep beams reinforced with a honeycomb steel mesh ［J］.Advances in Structural Engineering，2010，13（6）：989－999.

［9］Yang K H.Tests on lightweight concrete deep beams［J］.ACI Structural Journal，2010，107（6）：663－670.

［10］Yang K H，Ashour A F.Strut－and－Tie model based on crack band theory for deep beams ［J］.Journal of Structural Engineering，2011，137（10）：1030－1038.

［11］Rao G A，Kunal K.Studies on effect of size on strength and ductility of RC deep beams ［J］.Journal of Structural Engineering，2010，36（6）：393－400.

［12］Rao G A，Kunal K，Eligehausen R.Shear strength of RC deep beams ［C］／／ Proceedings of the 6th International Conference on Fracture Mechanics of Concrete and Concrete Structures，2007，2：693－699.

［13］中国工程建设标准化协会标准.纤维混凝土结构技术规程CECS 38：2004［S］.北京：中国计划出版社，2004.

［14］朱伟勇.正交与回归正交试验法的应用［M］.沈阳：辽宁人民出版社，1978.

［15］Tan K H，Tang C Y，Tong K.Shear strength predictions of pierced deep beams with inclined web reinforcement［J］.Magazine of Concrete Research，2004，23（l）：443－452.

［16］张宏战，黄承逵.钢筋钢纤维高强混凝土箍筋梁剪切延性分析［J］.大连理工大学学报，2005，45（3）：422－426.Zhang H Z，Huang C K.Study of ductility of steel fiber reinforced high－strength concrete beams with stirrups ［J］. Journal of Dalian University of Technology，2005，45（3）：422－426.

［17］赵国藩，彭少民，黄承逵，等.钢纤维混凝土结构［M］.北京：中国建筑工业出版社，1999.

［18］Mazars J，Pijaudier C G.Continuum damage theory application to concrete ［J］.Journal of Engineering Mechanics，1989，115：345－365.

［19］董哲仁.钢筋混凝土非线性有限元法原理与应用［M］.北京：中国铁道出版社，1993.