疲劳可靠度分析的概率密度演化方法

徐亚洲

（西安建筑科技大学 土木工程学院，西安 710055）

疲劳损伤及断裂问题是材料和结构失效的常见模式。有资料表明，70%～80%的金属结构破坏与疲劳损伤及断裂有关［1］。由于影响结构疲劳损伤及断裂的因素甚多且物理机制复杂，如材料性质、结构组成、荷载、参数估计、模型误差、使用环境等［2］，本质上均具有不可忽略的随机性。因此，采用可靠度的方法分析结构疲劳损伤就成为一种自然的选择。

疲劳可靠度分析理论一直是该领域的研究重点。针对传统的应力强度干涉模型的不足，Liao等［8］建议了可以考虑非线性损伤累积的动力干涉模型。倪侃等［9］同建立了疲劳可靠度的二维概率Miner准则。Le等［10］建议了一种未知载荷信息时对结构进行疲劳可靠性分析的方法。通过对已产生疲劳损伤的构件进行剩余寿命测试，并与同类新构件的疲劳寿命进行比较，据此间接地推断受损构件的疲劳载荷特性。Lu等［11］采用等效初始缺陷尺寸法（EIFS）进行了比例及非比例多轴加载条件下的疲劳寿命分析。王春生等［12］根据Bayes定理建立了既有钢桥疲劳可靠度更新模型。Pan等［13］采用gamma随机过程理论及Birnbaum－Saunders双变量概率分布分析了具有多个退化路径的疲劳寿命问题。Pipinato等［14］采用线弹性断裂力学研究了交通荷载损伤与地震损伤组合对桥梁疲劳寿命的影响。基于现场监测疲劳载荷谱，Guo等［15］对加固钢桥进行了疲劳可靠性分析。Sih［16－19］开展了一系列多尺度疲劳可靠性研究，涉及跨越纳观、介观、宏观尺度时材料的疲劳可靠性分析。

本文基于概率守恒原理［20］，从随机损伤演化的角度考察随机源和疲劳损伤的联合概率密度函数在循环加载过程中的变化规律，推导出描述联合概率密度函数在损伤变化率输运过程中满足的演化方程，给出了相应的差分数值解法。最后，通过常幅疲劳及二级加载变幅疲劳试验结果验证了方法的正确性。

1 随机疲劳损伤演化方程

1.1 随机疲劳损伤模型

疲劳损伤的一般形式可以表示为

其中：Y （n）为随机损伤过程；n为加载次数；Θ是确定随机损伤的随机参数集合；F是描述参数与随机损伤过程的一般变换，确定着加载次数、疲劳应力幅、累积损伤法则、S－N 关系等因素与疲劳损伤的关系。事实上，疲劳循环应力本身是一个连续过程，只是采用S－N 曲线计算疲劳损伤时将其离散为与加载次数有关的过程。此外，与疲劳寿命的数量级相比可以视加载参数为连续变量，故以下基于此进行基本方程的推导。

f（Θ ，n）为随机损伤变化率的形式解。疲劳损伤变化率如无解析结果，一般需要采用适当精度的差分格式对其进行离散。

疲劳损伤及其可靠性分析时，通常将不确定性区分为疲劳寿命的离散性和载荷的随机性，故取

式中：S为疲劳应力幅；Nf为疲劳寿命。

1.2 疲劳损伤的概率密度演化方程

将随机疲劳损伤视为一般随机过程，通过时变概率密度函数可以确定其概率结构的演化规律。为此，考虑初始随机性随疲劳损伤变化率输运时随机损伤与随机参数的联合概率密度函数的变化规律，基于概率守恒原理建立联合概率密度函数的演化方程，据此可实现随机疲劳损伤的演化规律分析。

记随机疲劳损伤与随机参数的联合概率密度函数为pYΘ（y，θ，n），考虑随机损伤演化过程中没有新的随机源产生，｛Y （n），Θ｝在定义域 ｛ΩY×ΩΘ｝上是概率保守系统，其中ΩY是随机损伤概率空间，ΩΘ为随机参数概率空间。

取 ｛ΩY×ΩΘ｝中任意控制体Ω，分析加载次数增量dn内控制体中联合概率密度函数pYΘ（y，θ，n）变化及其与边界概率流动的关系。加载次数增量dn内由损伤变化率经过随机损伤概率控制体边界∂ΩY输运的概率为

另一方面，控制体内联合概率密度函数pYΘ（y，θ，n）经过dn后变化为

对于概率守恒系统，经过控制体边界流入的概率应该等于控制体内概率的增量，故有

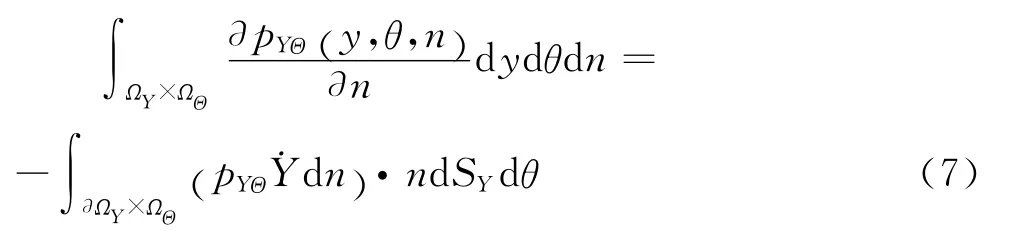
运用散度定理将面积分转化为体积分，引入随机损伤变化率的形式解＝f（Θ ，n），得

将式（8）代入式（7），注意到形式解fΘ，（ n）与y无关，则有

考虑控制体的任意性，即可得联合概率密度函数pYΘ（y，θ，n）的演化方程

其物理意义可以解释为加载开始时联合概率密度函数的概率分布已知。

上述随机损伤演化方程的推导类似于流体动力学中连续方程的推导，有关概率守恒及联合概率密度函数服从的演化方程的详细讨论可以参见文献［20－21］。

将pYΘ（y，θ，n）在随机参数概率空间ΩΘ上积分即可获得随机疲劳损伤的概率密度函数

至此，给出随机参数的初始概率分布及累积损伤法则，就可以方便地通过随机损伤演化方程获得其概率密度函数。进而，根据定义计算各阶特征量（均值、标准差等）和可靠度。

2 疲劳可靠度分析

2.1 基于损伤的疲劳可靠度

通过随机疲劳损伤概率密度演化方程求得其概率密度函数，再给定疲劳损伤失效的阈值Δ即可获得其可靠度

Pr｛··｝表示概率。通常疲劳损伤阈值Δ取为1。

2.2 数值方法

联合概率密度服从的演化方程是偏微分方程，通常无法获得解析解［22］。采用数值方法求解的具体步骤归纳如下：

1）确定影响疲劳损伤过程Y （n）的随机参数集Θ及其概率模型，获得离散点集Θq＝ ｛Θ1，q，Θ2，q…Θm，q｝，其 中 m 为随机变量数目，q ＝ 1，2…Nsel为选点数目，利用点集Θq求得损伤过程变化率（n）。

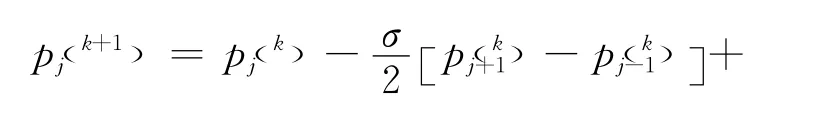
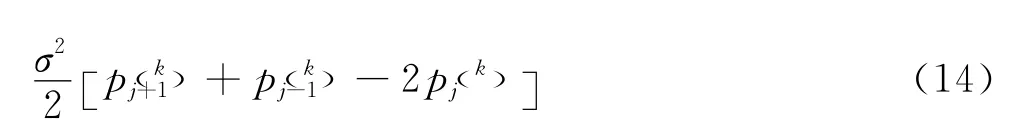
3）对pYΘ（y，θ，n）在Θ上积分可得pY（y ，n），利用式（13）求得给定损伤阈值Δ下的疲劳可靠度。

3 算例分析

3.1 常幅疲劳可靠度

常幅疲劳分析中唯一的随机参数为疲劳寿命Nf，采用Miner线性疲劳损伤准则可得累积疲劳损伤的具体表达式为：

式中：Nf是疲劳寿命，n是加载循环次数。

应力比为0.02，最大应力为281.2MPa时，LY12－CZ合金材料的11个归一化对数疲劳寿命试验结果见表1，其中归一化疲劳寿命由样本值Ni与均值¯N之比确定。试验疲劳可靠度由中位秩给出［23］，归一化对数疲劳寿命经过假设检验可知其服从正态分布，均值为1，标准差为0.304。等间距离散随机参数（疲劳寿命Nf）获得100个代表点，代入式（15）可得累积疲劳损伤的100个样本。根据随机疲劳损伤演化方程计算的概率密度演化曲面见图1。可以发现，加载起始时刻的疲劳损伤分布较为集中，随着加载次数的增加疲劳损伤的标准差逐渐增加，且损伤均值也逐渐增大，表明疲劳可靠性逐渐降低。值得注意的是，疲劳损伤均值及标准差均随加载次数的增加而增大。由于采用了线性累积损伤模型，相应的变异系数与常幅疲劳寿命的变异系数接近。

表1 LY12－CZ合金归一化疲劳寿命试验结果［23］

图1 常幅疲劳损伤概率密度曲面

给定损伤失效阈值为1，对疲劳损伤的概率密度函数值进行积分也可以获得疲劳可靠度，与试验可靠度的比较见图2。可见，计算结果与试验结果吻合良好。

图2 常幅疲劳可靠度分析结果

将疲劳损伤概率密度演化曲面积分可以获得累积概率分布函数，其累积概率等值线见图3。由于采用了线性损伤累积法则，疲劳损伤累积概率分布函数的等值线为直线。给定疲劳损伤阈值，与累积概率分布函数等值线族相交的点集对应的加载次数即为具有不同可靠度的疲劳寿命。此处取阈值为1，与累积概率为0.5的等值线相交处（图3中黑点）对应的无量纲加载次数为1。即50%的保证率下无量纲加载次数至1时发生疲劳破坏（损伤达到1）。给定损伤阈值后，加载次数越大，对应的疲劳可靠度越低，表现为交点对应的疲劳损伤累积概率等值线数值越小。相反地，给定加载次数，则损伤阈值越大对应的疲劳可靠度越高，表现为损伤阈值与加载次数交点处的等值线具有更大的累积概率值。如交点位于两条等值线之间可采用线性插值计算，也可以直接给出规定累积概率值的等值线进行分析。

3.2 低高二级加载变幅疲劳可靠度

低 高两级加载冷轧软钢弯曲疲劳试验结果见表2。第一级载荷为应力幅S1＝280.2MPa时固定循环n1＝4×105次，然后在应力幅为S2＝329.9MPa的第二级载荷下加载至试件疲劳破坏，第二级加载次数为n2。两级载荷对应的常幅试验对数疲劳寿命均服从正态分布，其中第一级载荷下的对数疲劳寿命为lgNf1～N（6.009，0.256） ，第二级载荷下的对数疲劳寿命lgNf2～N（5.274，0.190）。

表2 低高两级加载软钢疲劳寿命试验结果［24－25］

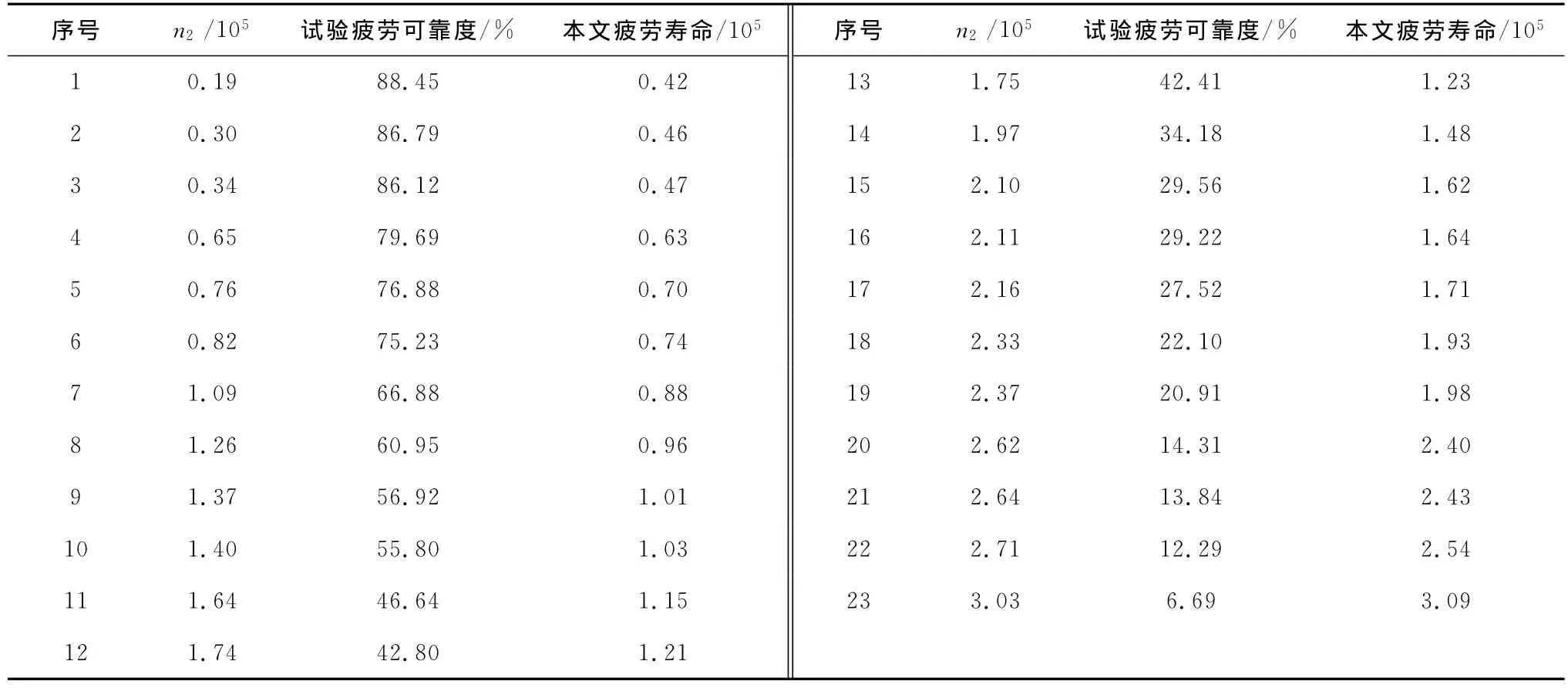
表2 低高两级加载软钢疲劳寿命试验结果［24－25］

序号 n2／105 试验疲劳可靠度／% 本文疲劳寿命／105 序号 n2／105 试验疲劳可靠度／% 本文疲劳寿命／105 1 0.19 88.45 0.42 13 1.75 42.41 1.232 0.30 86.79 0.46 14 1.97 34.18 1.483 0.34 86.12 0.47 15 2.10 29.56 1.624 0.65 79.69 0.63 16 2.11 29.22 1.645 0.76 76.88 0.70 17 2.16 27.52 1.716 0.82 75.23 0.74 18 2.33 22.10 1.937 1.09 66.88 0.88 19 2.37 20.91 1.988 1.26 60.95 0.96 20 2.62 14.31 2.409 1.37 56.92 1.01 21 2.64 13.84 2.4310 1.40 55.80 1.03 22 2.71 12.29 2.5411 1.64 46.64 1.15 23 3.03 6.69 3.0912 1.74 42.80 1.21

二级加载变幅疲劳分析中的随机参数为疲劳寿命Nf1和Nf2，仍然可以通过Miner疲劳损伤准则计算累积疲劳损伤

式中：n1＝4×105。物理上考虑，如第一级加载时试件即发生疲劳破坏（Nf1＜n1），此时无法进行第二级加载，相应的损伤值等于1。如不考虑这一事实，继续根据第二级加载计算损伤值在物理上是不真实的。因此，如抽样所得第一级载荷对应的常幅疲劳寿命Nf1＜n1，则取相应的累积疲劳损伤Y＝1，相当于设置了一个吸收边界条件，表示在n1次加载下试件已经疲劳破坏。

本文方法计算的二级加载疲劳损伤概率密度演化曲面见图4，试验疲劳可靠度和计算可靠度的比较见图5，相应的累积概率分布函数等值线见图6。与等幅疲劳分析结果类似，加载次数较小时疲劳损伤分布较为集中。随着加载次数的增加，疲劳损伤均值及标准差逐渐增大。试验疲劳可靠度与计算结果吻合较好。预测偏差的原因在于：一方面，尽管算例试验样本数目达23个，但据此计算可靠度本身可能产生误差；另一方面，二级低高加载本质上属于变幅疲劳试验，仅根据两级载荷各自的常幅疲劳寿命分布参数，且采用线性Miner法则计算累积损伤可能带来模型误差。

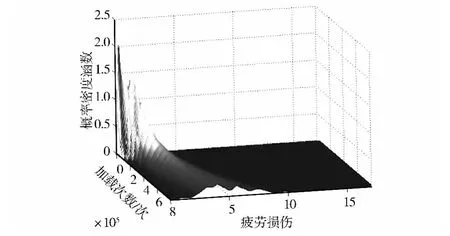
图4 变幅疲劳损伤概率密度曲面

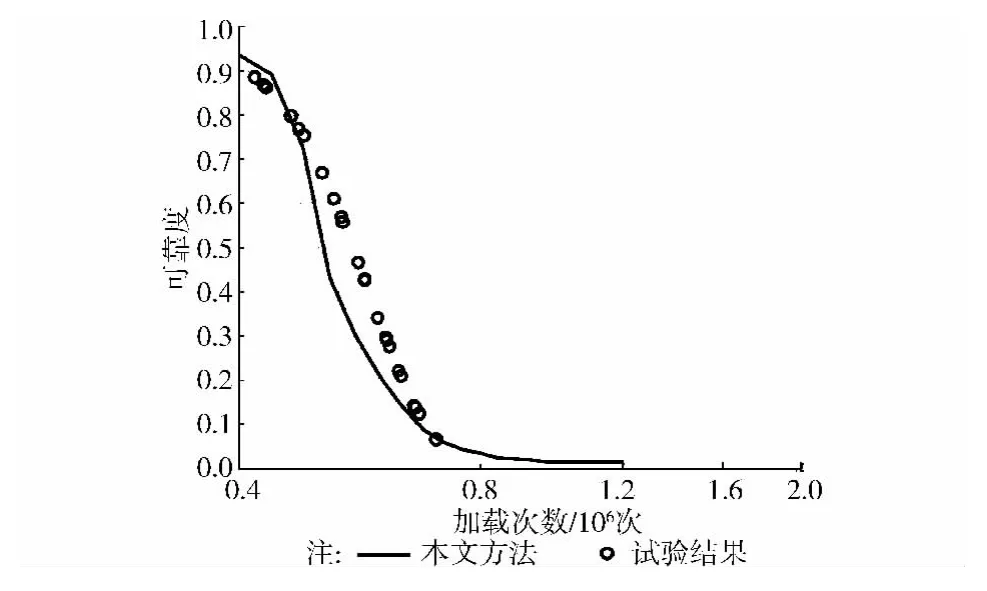
图5 变幅疲劳可靠度分析结果

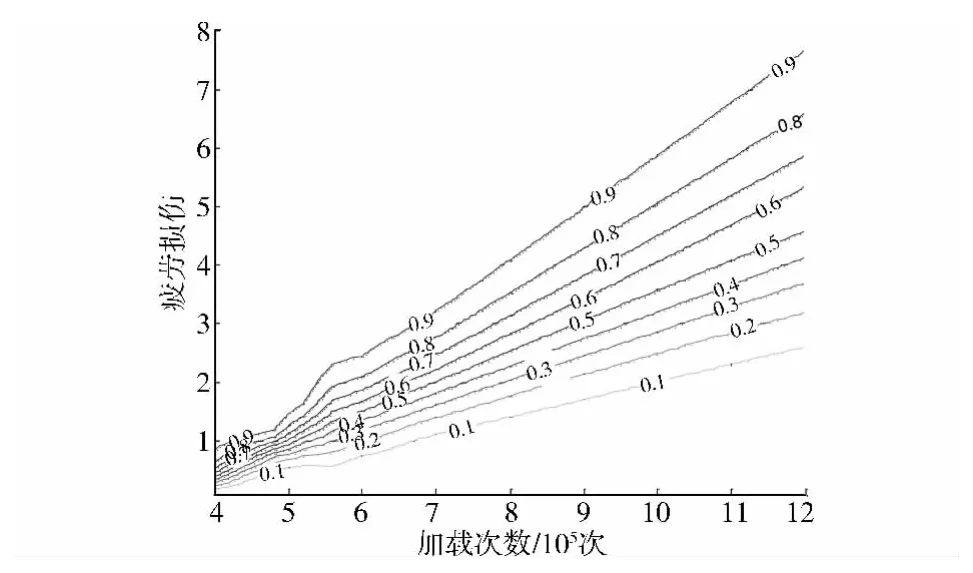
图6 变幅疲劳损伤累积概率分布函数等值线

4 结论

考虑疲劳寿命变异性和载荷随机性为疲劳损伤的随机源，基于概率守恒原理推导出随机参数与疲劳损伤联合概率密度函数的损伤演化方程。采用两步Lax－Wendroff差分格式可以获得联合概率密度函数的数值解，对其在随机参数空间进行积分即可获得随机疲劳损伤的概率密度演化信息。给定损伤失效阈值，可以进一步计算其疲劳可靠度。此外，据此计算的疲劳损伤累积概率分布等值线可用以分析给定损伤阈值时疲劳寿命的可靠度，也可以分析给定加载次数时不同损伤阈值条件下的疲劳可靠度。

根据LY12－CZ合金材料常幅试验结果确定其对数疲劳寿命服从正态分布，给出其参数估计值。采用随机损伤演化方程获得随机疲劳损伤概率密度函数的数值解，取损伤阈值等于1计算的疲劳可靠度与试验疲劳可靠度吻合良好。此外，基于冷轧软钢两级载荷各自常幅疲劳寿命分布参数，采用Miner准则计算累积疲劳损伤，根据疲劳损伤概率密度演化方法计算的低高两级加载弯曲疲劳可靠度与试验结果吻合较好。

［1］Guangwei M.The committee on fatigue and fracture reliability of the committee on structural safety and reliability of the structural division［J］.Journal of the Structural Division，1982，108：3－23.

［2］Svensson T. Prediction uncertainties at variable amplitude fatigue［J］.International Journal of Fatigue，1997，17：295－302.

［3］Boehm F，Lewis E E.A stress－strength interference approach to reliability analysis of ceramics：Part I－fast fracture ［J］.Probabilistic Engineering Mechanics，1992，7（1）：1－8.

［4］Liu W K，Chen Y，Belytschko T，et al.Three reliability methods for fatigue crack growth ［J］.Engineering Fracture Mechanics，1996，53（5）：733－752.

［5］Oh K P.A diffusion model for fatigue crack growth［J］.Proceedings of the Royal Society A：1979，367：47－58.

［6］Leonel E D，Chateauneuf A，Venturini W S，et al.Coupled reliability and boundary element model for probabilistic fatigue life assessment in mixed mode crack propagation ［J］.International Journal of Fatigue，2010，32：1823－1834.

［7］Xiang Y B，Liu Y M.Application of inverse first－order reliability method for probabilistic fatigue life prediction［J］.Probabilistic Engineering Mechanics，2011，26：148－156.

［8］Liao M，Xu X F，Yang Q X.Cumulative fatigue damage dynamic interference statistical model ［J］.International Journal of Fatigue，1995，17（8）：559－566.

［9］倪侃，高镇同.疲劳可靠性二维概率MINER准则［J］.固体力学学报，1996，17（4）：341－346.Ni K， Gao Z T. Two－dimensional probabilistic MINER’s rule in fatigue reliability ［J］. Acta Mechanica Solida Sinica，1996，17（4）：341－346.

［10］Le X B，Peterson M L.A method for fatigue based reliability when the loading of a component is unknown［J］.International Journal of Fatigue，1999，21（6）：603－610.

［11］Lu Z Z，Xiang Y B，Liu Y M.Crack growth－based fatigue－life prediction using an equivalent initial flaw model.Part II：Multiaxial loading ［J］.International Journal of Fatigue，2010，32（2）：376－381.

［12］王春生，刘鑫，俞欣，等.基于无损探测信息的既有钢桥构件疲劳可靠度更新评估［J］.土木工程学报，2010，43（8）：81－87.Wang C S，Liu X，Yu X，et al.Fatigue reliability updating evaluation using nondestructive inspections for existing steel bridges ［J］.China Civil Engineering Journal，2010，43（8）：81－87.

［13］Pan Z Q，Balakrishnan N.Reliability modeling of degradation of products with multiple performance characteristics based on gamma processes ［J］.Reliability Engineering and System Safety，2011，96（8）：949－957.

［14］Pipinato A， Pellegrino C， Modena C. Fatigue assessment of highway steel bridges in presence ofseismic loading［J］.Engineering Structures，2011，33：202－209.

［15］Guo T， Chen Y W. Field stress／displacement monitoring and fatigue reliability assessment of retrofitted steel bridge details［J］.Engineering Failure Analysis，2011，18：354－363.

［16］Sih G C.Use specification of multiscale materials for life spanned over macro－，micro－，nano－，and pico－scale［J］.Theoretical and Applied Fracture Mechanics，2010，53（2）：94－112.

［17］Sih G C.Scale shifting laws from pico to macro in consecutive segments by use of transitional functions［J］.Theoretical and Applied Fracture Mechanics，2010，53（3）：165－179.

［18］Sih G C.Principle of least variance for dual scale reliability of structural systems ［J］.Theoretical and Applied Fracture Mechanics，2010，54（3）：137－140.

［19］Sih G C.Multiscale reliability of physical systems based on the principle of least variance［J］.Theoretical and Applied Fracture Mechanics，2011，55（1）：1－19.

［20］Li J，Chen J B.The principle of preservation of probability and the generalized density evolution equation［J］.Structural Safety，2008，30（1）：65－77.

［21］李杰，陈建兵.随机结构非线性动力反应的概率密度演化分析［J］.力学学报，2003，35（6）：716－722 Li J，Chen J B.The probability density evolution method for analysis of dynamic nonlinear response of stochastic structures ［J］.Acta Mechanica Sinica，2003，35（6）：716－722.

［22］Li J，Chen J B.The probability density evolution method for dynamic response analysis of non－linear stochastic structures ［J］.International Journal for Numerical Methods in Engineering，2006，65（6）：882－903.

［23］姚卫星.结构疲劳寿命分析［M］.北京：国防工业出版社，2003：209－210.

［24］Levy J C.Cumulative damage in fatigue.A method of investigation economical in specimens ［J］.Engineering，1955，179（6）：724－726.

［25］倪侃，张圣坤，高镇同.二维概率MINER准则的试验数据验证［J］.机械强度，1997，19（3）：52－56.Ni K，Zhang S K，Gao Z T.Experiment verification of two－dimensional probabilistic miner’s rule［J］.Journal of Mechanical Strength，1997，19（3）：52－56.