等效静力风荷载背景和共振之间的耦合效应

柯世堂，王法武，周 奇，周志勇，赵 林

（1.南京航空航天大学 土木工程系，南京 210016；2.汕头大学 风洞实验室，广东 汕头 515063；3.同济大学 土木工程防灾国家重点实验室，上海 200092）

在求解大跨度屋盖结构的风致响应和等效静风荷载（ESWLs）时，可以根据结构的动力特性和风荷载的自身特征，将响应分成背景和共振两个分量求解，然后采用一定的组合方法来获得总风致响应。该思路要求在求解时考虑背景与共振、共振与共振、背景与背景之间的三层耦合项，传统的基于荷载响应相关方法［1］（LRC）和惯性风荷载方法［2］（IWL）的三分量方法无法精确求解这三层耦合项。很多学者对此进行了研究，并提出了有效的改进方法，例如Holmes等［2－3］和Irwin［4］最早提出了背景和共振分量的计算方法；Zhou等［5］、Chen等［6］和 Zhang［7］将这一方法进一步发展，明确了三分量方法的求解思路；随后针对共振分量求解中的耦合效应问题，周晅毅等［8］、顾明等［9］、陈波等［10］、谢壮宁等［11］、余世策等［12］、梁枢果等［13］和柯世堂等［14］对三分量方法 进行了不同的改进，其中顾明等在中国最早采用三分量方法对上海金茂大夏、上海铁路南站等结构进行ESWLs分析，并对比阵风荷载因子法（GLF）结果认为三分量法的结果更加精确合理；陈波等提出的Ritz－POD方法可进行风振响应精细化分析；谢壮宁等基于LRC的完全二次型组合获取结构的风振响应和ESWLs，不区分背景和共振分量。这些改进方法更好的解决了大跨屋盖结构风致响应和ESWLs的两层耦合项问题：1）共振模态的选择及模态间的耦合项求解难题；2）采用准静力方法求解背景分量以考虑所有模态对于背景响应的贡献。对于背景与共振模态之间的耦合效应，缺乏简单有效的计算方法，因此大多直接采用SRSS方法组合背景和共振分量来获得总脉动风致响应，这一作法对于背景和共振模态有较好分离的结构（高层建筑、高耸结构等）误差较小，然而对于某些大跨度空间柔性结构，这一耦合分量理论上是需要考虑的。

本文基于模态加速度法和荷载响应相关原理，推导出结构ESWLs的真实理论组合公式，首次定义耦合恢复力协方差矩阵参数，提出用于补偿背景和共振模态间耦合项的一致耦合方法（CCM）来求解结构的ESWLs，该方法避开了复杂的相关系数求解过程，且思路清晰，作用机理明确。并以某大跨度屋盖结构为例，采用一致耦合方法进行风致响应和ESWLs计算，通过与全模态CQC计算结果进行对比分析，深入揭示了该结构风致响应中背景和共振耦合分量的参与机理，验证了本文方法的高精度和有效性，并为此类结构风致响应和ESWLs的精确求解和机理研究提供新的思路。

1 背景和共振耦合项的理论推导

1.1 CCM方法的提出

柔性结构在风荷载激励下的随机动力响应方程可表达为：

式中：｛p（t）｝代表外部风荷载激励向量；M、C、K 为结构的质量、阻尼和刚度矩阵（t）（t）、y（t）分别为节点的加速度、速度和位移向量。

使用模态叠加原理，式（1）可表达成

式中：qi（t）表示第i阶模态的广义位移向量；fi（t）表示第i阶模态的广义力向量。

对于柔性结构的风致动力响应来说，高阶模态共振响应通常可以忽略，这样动态位移可以表示为

式中：Φ 为振型矩阵；φi为第i阶振型向量；qi，b（t）为仅包含准静力贡献的第i阶背景位移响应向量；qi，r（t）为仅包含共振效应贡献的第i阶共振位移响应向量；｛y（t）｝b，n为包含所有模态准静力贡献的背景响应向量；｛y（t）｝r，m为仅包含共振效应贡献的前m阶模态共振位移响应向量。

通常有2种频域求解方法来计算式（3）中总的脉动风响应向量的均方差：

1）采用SRSS方法来组合背景和共振分量，可以表达为

式中：σt、σb，n、σr，m分别代表了响应向量｛y（t）｝、｛y（t）｝b，n、｛y（t）｝r，m的均方差。

其中背景分量可以作为准静力响应，采用LRC方法来求解，共振分量采用惯性风荷载方法来计算。这一方法不能考虑背景和共振之间的模态耦合项，也不能很好的考虑共振模态之间的耦合项。

2）求解总脉动响应的组合方法为

背景分量σb，m是前m 阶背景位移向量｛y（t）｝b，m的均方差；ρr，b为背景分量和共振分量之间的相关系数，可以用下式计算

从式（5）中可以发现，背景分量仅仅包含前m阶模态准静力贡献，相应地，背景和共振分量之间的交叉项也是仅仅包含前m阶模态的贡献。

基于SRSS组合的三分量法不能考虑背景和共振之间的交叉项，这对于相关系数ρr，b很小的结构是可以接受的，然后由于式（6）计算过程的复杂，并且没有发展交叉项响应的ESWLs计算理论，因此在大多数的柔性结构风致响应和ESWLs计算中都不去考虑，其对于某些强耦合结构是不合理。

根据式（3）可以将脉动风总响应均方差精确的表达为

式中：σc，nm代表前n阶背景分量和前m 阶共振分量的交叉项。

和传统方法最大不同在于式（7）能考虑所有模态的准静力贡献，前m阶共振模态之间的耦合效应，n阶背景模态和前m阶共振模态之间的交叉项。

我们知道背景分量可以基于外荷载激励的协方差矩阵，并采用LRC原理进行求解。借鉴这一思路，首次提出广义恢复力协方差矩阵、共振恢复力协方差矩阵和耦合恢复力协方差矩阵这一概念，统一引入LRC方法来求解共振和交叉项分量，进而使得相应的ESWLs的求解有了理论基础。这样，式（7）变成：

式中 ［Cpp］t为广义恢复力协方差矩阵；［Cpp］b为外荷载协方差矩阵；［Cpp］r共振恢复力协方差矩阵；［Cpp］c为耦合恢复力协方差矩阵；I为影响线矩阵。

这样可以进一步变化耦合恢复力协方差矩阵的表达式为

这样我们可以分别求解背景、共振和耦合恢复力协方差矩阵，在基于LRC方法获得各响应分量和ESWLs分量。下面以共振分量为例，给出了其风振响应和等效静风荷载各分量的推导过程。

1.2 背景、共振和耦合项恢复力协方差矩阵的推导

仅包含共振分量的第i阶广义模态响应为

则第i阶和第j阶广义共振模态响应的互功率谱为

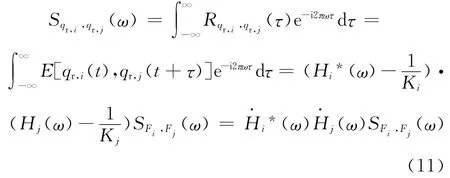
从式（11）中可以发现，广义共振模态响应的求解关键是确定广义共振频响传递函数。

综合以上各式，广义共振模态响应协方差矩阵可表示为

式中SAA为经POD［15］分解获得的前s阶时间坐标函数A（t）互功率谱矩阵，用作降阶处理。

应用模态展开理论，结构仅包含共振分量的弹性恢复力可表示为

结合式（12）、（13），得到 ｛Peqq｝r的互协方差矩阵 ［Cpp］r为

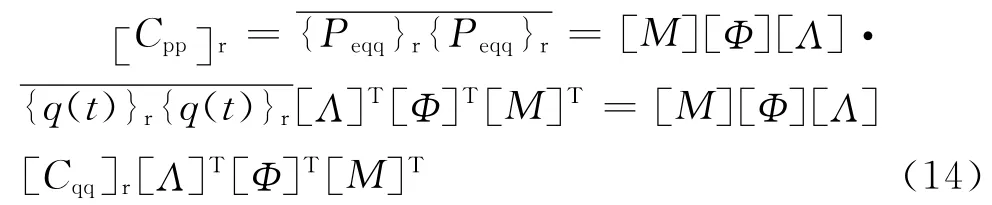
从以上的推导容易看出，｛Peqq｝r是仅包含共振分量的弹性恢复力向量，其精确程度取决于计算｛q（t）｝r时所取的模态阶数和系统的动力特性；同理，把式（14）中求解 ［Cqq］r所需的共振频响函数换成广义频响函数矩阵H即可得到总弹性恢复力协方差矩阵［Cpp］t；在通过风洞试验获得风荷载时程直接获取背景恢复力协方差矩阵 ［Cpp］r；由式（8）定义的耦合弹性恢复力协方差矩阵 ［Cpp］c，其计算公式为

1.3 背景、共振及背景和共振耦合项各分量的求解

至此，求解共振、背景、耦合响应及其等效静风荷载都可以转化为求系统在相应恢复力作用的准静力响应，进而可以利用LRC原理来计算。以共振分量为例给出求解过程

当I为柔度矩阵时，r（t）即为结构的共振响应，其响应的协方差矩阵为

则结构的共振响应为

式中，diag（·）表示取矩阵的对角元素组成列向量。

响应Ri的对应的共振等效静风荷载为

综上可知，采用这一思路可以求解背景和共振耦合分量的风致响应和等效静风荷载，只需将式（17）和（19）中的 ［Cpp］r换成 ［Cpp］c。需要注意的一点是，由式（17）求解的耦合响应协方差矩阵中的元素可能会出现负数的情况，分析其原因：元素为正时说明忽略耦合分量会低估结构的响应，为负时说明忽略耦合分量会高估结构的响应。在代入到公式（18）求解耦合响应时一律按正值代入，但在组合时必须要考虑其正负影响。

1.4 总风致响应和ESWL的组合

最后组合脉动风总响应

式中σr、σb和σc分别为共振、背景和耦合响应分量，应该注意的是对于耦合分量的组合，一定要考虑其正负影响。

采用线性组合方式组合各分量得到总的等效静力风荷载，这样可以保证总的等效静力风荷载是真实的荷载分布形式，并且在该荷载作用下，能确保控制点和非控制点的响应都与峰值响应一致。

式中：Peb、Pec为等效静力风荷载背景和耦合分量；WB、WR、WC分别为Per、Peb和Pec的权值系数。

下面验证由总等效静力风荷载引起的静力响应的有效性：

推导可知本文方法计算的结构风振响应结果正确，则其等效静风荷载一定准确无误。

2 算例分析

某大跨度屋盖结构形式新颖（见图1），全长228m，宽90m，屋顶结构采用斜放四角锥钢网架结构，整个双向曲面屋顶由6根“蘑菇柱”支撑，“蘑菇柱”均匀分布，很好的分散屋顶传来的荷载。图1中标出的A～F6个节点是该结构上具有代表性的典型节点，文中的分析均以这6个节点的响应特征为例。

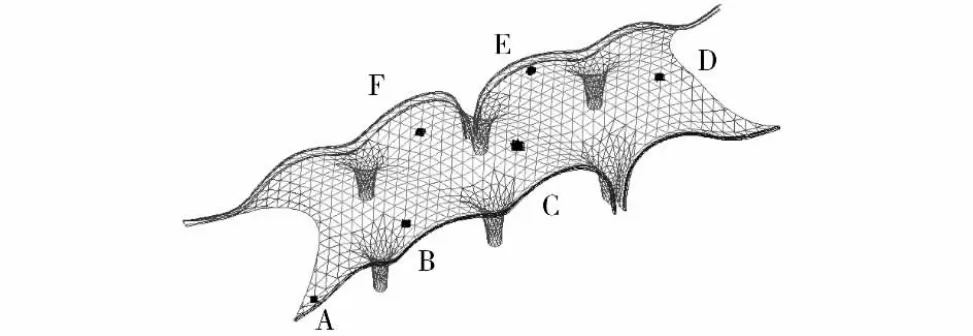
图1 博物馆计算模型及典型节点示意图

图2给出了结构前300阶自振频率的分布情况，可以看出结构的自振频率较低，在1.5～13Hz频率之间存在300阶频率，特别在10～13Hz之间分布了200阶频率，其分布十分密集。计算时取10m高的基本风速为60m／s，阻尼比为0.02，峰值因子统一采用3.5。

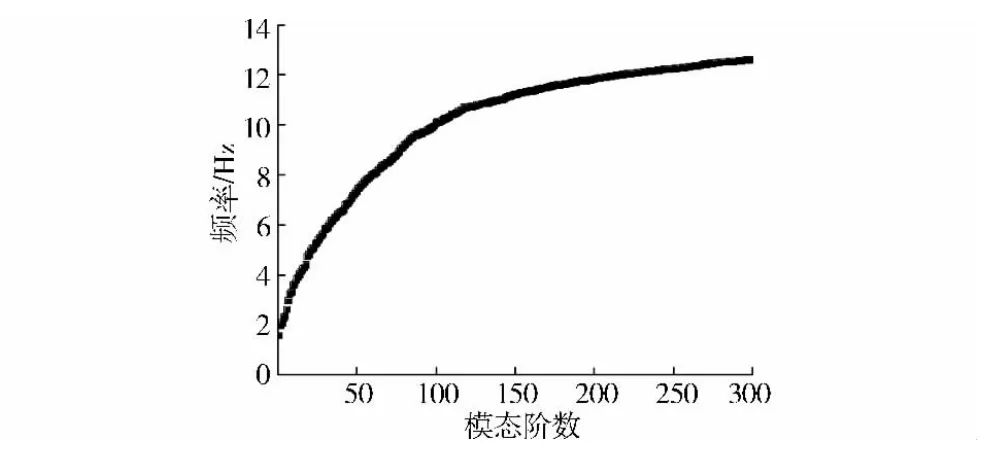
图2 结构固有频率分布图

图3给出了典型节点E的位移响应功率谱密度函数图，从图中可以看出，该节点的风振响应中第1阶模态贡献的能量很小，主要是由5、9、17和30阶模态贡献能量，且准静力效应贡献的背景分量不可忽略，但从响应功率谱图中无法直接观察背景和共振之间的交叉项所占比重的影响，需要进一步分析。

图3 节点A位移响应功率谱图

采用本文提出的CCM方法、改进的三分量方法（即考虑了共振模态之间的耦合效应）以及基于全模态CQC方法对结构进行频域计算，提取这6个典型节点的响应根方差。表1给出了这3种方法计算的响应结果，可以发现：1）对于博物馆这类大跨空间结构，必须考虑多阶模态的贡献，对每个结构应具体分析后确定参振模态数目，通过逐渐增加计算模态数并和全模态CQC法的计算结果（即为精确解）对比确定该博物馆结构风振分析采用100阶即可；2）采用改进的三分量方法的计算结果对于博物馆结构的脉动风致响应来说误差较大，其中E点的误差最大，达到了－14.6%，说明忽略背景和共振模态之间的耦合分量对于该结构来说有时偏于危险，需要引起重视；3）本文的CCM法计算结果和全模态CQC计算的精确解的结果吻合的较好，最大的误差在F点，仅为1.94%，绝对平均误差连1%都不到，说明本文方法具有较高的精度。

表1 典型节点脉动风致响应根方差 mm

为了研究获得的等效风荷载的精度及有效性，分别给出本文方法和GLF＋IWL的三分量法所得到的等效静风荷载结果与在此等效静风荷载作用下的结构响应结果。从图4、5中可以看出，采用本文方法所得到的等效静风荷载结果略小于三分量的结果，但应用这两种方法所得到的结构等效静风响应结果在控制点上的结果是完全一致的。不仅如此，通过与精确解的比较表明：本文方法在保证控制点等效的同时，还保证了结构其他部位的响应更接近于实际可能发生的最不利响应，而传统的三分量方法却无法做到这一点。进一步说明对于某些大跨度屋盖结构来说，背景和共振交叉项的贡献不能忽略。

图4 等效静风荷载计算结果

图5 等效静风响应计算结果

3 结语

系统地讨论了大跨度屋盖结构等效静风荷载研究的关键问题，即如何解决共振模态之间的耦合效应、背景和共振模态之间的耦合效应问题。从随机振动理论出发，推导出用于补偿共振与背景间耦合分量的一致耦合法。并将其用于某大型博物馆结构的风致响应及等效静风荷载分析，验证了CCM法相比传统的三分量方法可以更加精确的求解结构的背景、共振及交叉项响应，并赋予等效静风荷载以更明确的物理意义。分析结果表明对于某些大跨度屋盖结构，不仅要考虑各共振模态之间的耦合效应，背景和共振之间耦合效应同样不能忽略，而本文的CCM方法可以很好的解决这一问题。

［1］Davenport A G.Gust loading factor［J］.Journal of the Structural Division，1967，93（ST3）：11－34.

［2］Holmes J D.Wind loading of parallel free－standing walls on bridges，cliffs，embankments and ridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89（14）：1397－1407.

［3］Holmes J D，Kasperski M.Effective distributions of fluctuating and dynamic wind loads［J］.Transactions of the Institution of Engineers， Australia， Civil Engineering，1996，38：83－88.

［4］Irwin P A.The role of wind tunnel modeling in the prediction of wind effects on bridges［C］／／Bridge aerodynamics，Balkema，Rotterdam，The Netherlands，1998：59－85.

［5］Zhou Y，Kareem A，Gu M.Equivalent static buffeting laods on structures ［J］. Journal of Structural Engineering，2000，126（8）：989－992.

［6］Chen X，Matsumoto M，Kareem A.Aerodynamic coupling effects on flutter and buffeting of bridges［J］.Journal of Engineering Mechanics，2000，126（1）：17－26.

［7］张相庭.国内外风荷载规范的评估和展望［J］.同济大学学报，2002，30（5）：539－543.Zhang X T.Evaluation and prospect for wind loading codes at home and abroad ［J］.Journal of Tongji University，2002，30（5）：539－543..

［8］周晅毅，顾明.上海铁路南站屋盖结构风致抖振响应参数分析［J］.同济大学学报，2006，34（5）574－579.Zhou X Y，Gu M.Parametric analysis of wind－induced buffeting responses of roof structure of Shanghai south railway station ［J］.Journal of Tongji University，2006，34（5）574－579.

［9］顾明，周晅毅，黄鹏.大跨屋盖结构风致抖振响应研究［J］.土木工程学报，2006，39（11）：37－42.Gu M，Zhou X Y.A study on the wind－induced buffeting responses of large－span roof structures ［J］.Journal of Civil Engineering，2006，39（11）：37－42.

［10］陈波，武岳，沈世钊.大跨度屋盖结构等效静力风荷载中共振分量的确定方法研究［J］.工程力学，2007，24（1）：51－55，66.Chen B，Wu Y，Shen S Z.Study of the resonant component of equivalent static wind loads on large span roofs［J］.Engineering Mechanics，2007，24（1）：51－55，66.

［11］谢壮宁，倪振华，石碧青.大跨度屋盖结构的等效静风荷载［J］.建筑结构学报，2007，28（1）：113－118.Xie Z N，Ni Z H，Shi B Q.Equivalent static wind loads on large span roof structures［J］.Journal of Building Structures，2007，28（1）：113－118.

［12］余世策，楼文娟，孙炳楠.开孔结构屋盖风致响应的模态分析法［J］.应用力学学报，2009，26（1）：76－81.Yu S C，Lou W J，Sun B N.Modal analysis to windinduced response for roof structures with wall opening［J］.Journal of Applied Mechanics，2009，26（1）：76－81.

［13］梁枢果，吴海洋，郭必武，等.大跨度屋盖结构等效静力风荷载数值计算方法［J］.华中科技大学学报，2008，36（4）：110－114.Liang S G，Wu H Y，Guo B W，et al.Numerical calculation of evaluating equivalent static wind loads on long span roof structures［J］.Journal of HUST，2008，36（4）：110－114.

［14］柯世堂，葛耀君，赵林，等.大型冷却塔结构的等效静力风荷载［J］.同济大学学报，2011.8，39（8），1132－1137.Ke S T，Ge Y J，Zhao L，et al.Equivalent static wind loadings of large cooling towers［J］.Journal of Tongji University，2011，39（8）：1132－1137.

［15］Ke S T，Ge Y J，Zhao L，et al.A new methodology for analysis of equivalent static wind loads on super－large cooling towers ［J］.Journal of Wind Engineering ＆Industrial Aerodynamics，2012，111（3）：30－39.