基于浮长线分析组织变化与织物厚度的关系
黄锦波,李启正,葛彩虹,范丽霞,张红霞
(浙江理工大学 a.材料与纺织学院;b.先进纺织材料与制备技术教育部重点实验室;c.杂志社,杭州310018)
在服用织物的生产织造过程中,厚度是重要指标之一。它直接影响着织物的外观、手感及保暖性能,同时也会造成某些织物物理机械性能的改变[1-2]。依据客户对产品要求的不同,织造工艺有所差别,织物的厚度会发生变化。在实际生产过程中织物组织的变化同样也会对厚度产生影响。合理调配经纬密度及组织可以达到节约原料降低成本的目的,因此,本研究拟对组织结构对织物厚度的影响展开探讨。
织物厚度的影响因素很复杂[3],很难做到系统的描述和预测,Peirce最早利用几何学的方法对机织物结构进行描述[4-5]。织物结构即为织物中经、纬纱线交织的空间形态结构。因其描述结构模型对纱线的性能都有特殊的要求,难以应用于实际织物厚度的测试。而后人们利用织物的结构相对织物几何结构进行分析,这是近代比较常用的方法。但因其假设的纱线是不可压缩与变形的圆柱体,同样无法对织物的厚度做出合理的分析[6-7]。本研究避开了经纬纱交织而造成的纱线形态的不可预测性,从织物交织点对浮长的控制着手,对单位面积内织物组织交叉点数的不同而带来的厚度变化进行理论分析和探究。
1 试验
1.1 试样准备
所选试样皆是以98.4 dtex×2(60S/2)棉纱为经纱,184.5 dtex(32S)咖啡色涤纶短纤纱为纬纱。织造机上经密为 400根/10 cm,机上纬密为 320根/10 cm。试样织造张力设定一致,制得了组织不同的4块样品。试样组织结构分别为平纹斜纹和五枚缎纹。
1.2 厚度测试
试样均在温度(20±2)℃、相对湿度(65±2)%的条件下进行厚度和显微镜浮长测试。
织物厚度测试参考国家标准GB/T 3820—1997《纺织品和纺织制品厚度的测定》进行。试验仪器选用YG(B)141D数字式织物厚度仪。测试时加压压力为1 kPa,加压时间为10 s,通过多次测量获得织物的厚度平均值。
1.3 纱线直径与浮长测定
织物中经纬纱线直径与浮长测试试验选用Leicam165c显微镜,采集在计算机上观察到的一定放大倍数下的纱线图像[8],观察试样经纬纱交织规律和经纬纱直径。
2 结果与分析
2.1 织物厚度测试
厚度测试结果见表1。
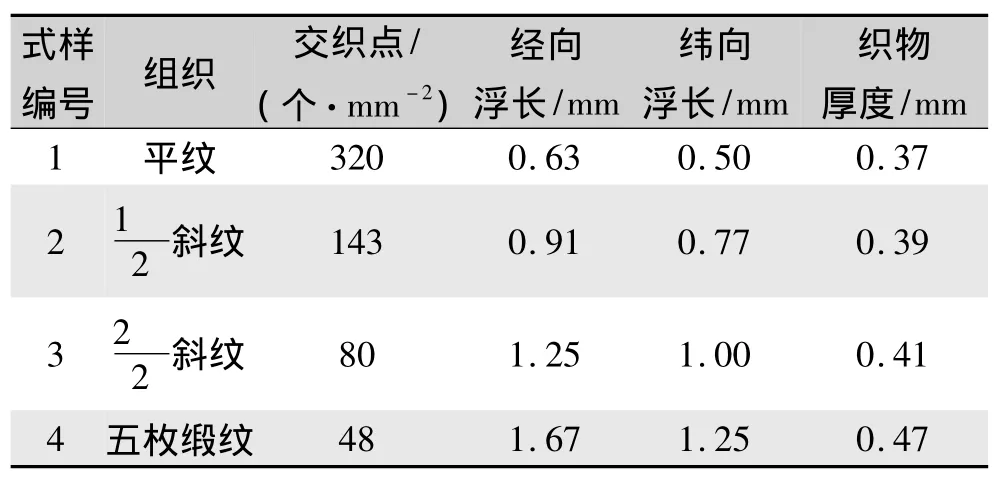
表1 不同组织结构的织物试样Tab.1 Fabric samples with different weaves
在原料与加工工艺相同的情况下,织物的组织变化直接影响着织物的厚度。如表1所示,组织为平纹的织物厚度仅0.37 mm,而随着织物交织点数的减少,织物的厚度也逐渐递增。当织物为五枚缎纹时,织物的厚度达到了0.47 mm。这是因为组织的变化,直接对单位面积内织物的交织点数量产生了影响。平纹组织单位面积内交织点个数最多,交织点个数多达320个/cm2,是缎纹组织的6倍多。织物中纱线浮长是交织点数和经纬密的共同作用,由于设定的经纬密参数一致,所以表1的浮长长度与经纬向交织点数呈反比关系。文中浮长长度皆指织物中一个交织点同下一个交织点间的距离L,如图1所示。

图1 经纬纱交织浮长示意Fig.1 Schematic diagram of weaving floating length of warp and weft yarns
为了进一步分析交织点数与织物厚度的关系,试验计算出4个试样组织循环倍数的最小公倍数60×60的组织循环内经纬纱交织点次数,并与织物厚度作出关系曲线,如图2所示。
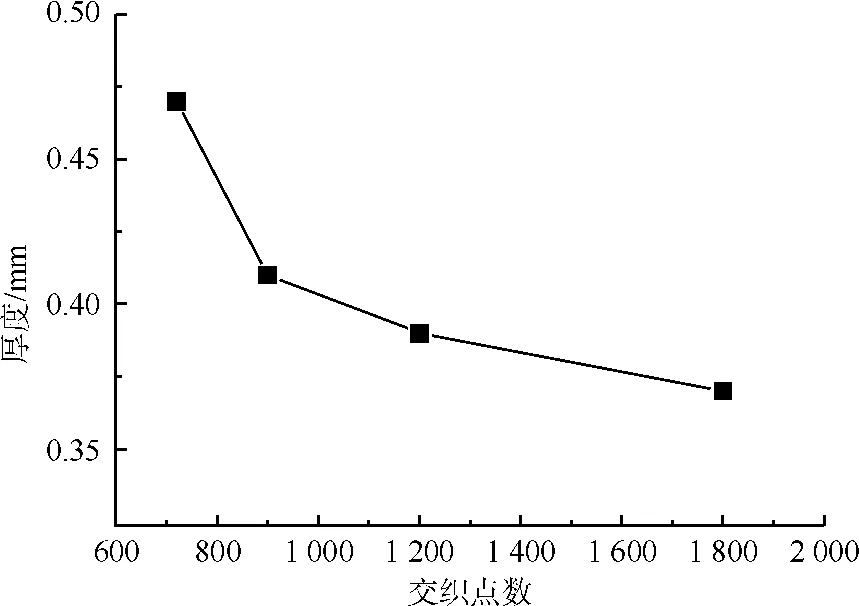
图2 60×60组织循环内经纬交织点数与厚度的关系Fig.2 Relationship between fabric interwoven points and thickness
从图2可以看出,织物单位面积内交织点的多少与织物的厚度大致呈反比趋势,织物中的交织点数多,则织物厚度小,随着交织点数量的减少,织物厚度增加。交织点的多少同织物经纬纱的浮长有着直接的关系,为了观察不同组织的浮长,在显微镜下观察了试样表面平面图(图3)。
从图3可以发现,平纹织物交叉点数最多,纱线类似于波浪线在经纬纱之间交错,经纬纱的浮长受到有效控制;斜纹次之,缎纹受到经纬纱交错控制最少。

图3 显微镜下不同组织试样Fig.3 Samples with different weaves under the microscope
从图3的几种基础组织中纱线的屈曲状态可以发现,织物经纬纱线交织过程中,纱线的几何结构会发生变化,这与纱线浮长受到有效控制的多少有关。平纹织物交叉点最多,交叉点间不受控或控制较小的浮长约为1个经纱直径的长度,其纱线的压扁系数e(e=b/a)较小,其中b为交叉纱线变形后的短轴长,a为交叉纱线的长轴长。斜纹由于相连两个交叉点之间浮长大于1,且交叉点的控制范围没有得到增强,所以纱线离交叉点较远的点压扁系数较大,织物较厚。缎纹的浮长更长,交叉点控制能力对整个浮长进一步减弱,所以缎纹织物相对于平纹和斜纹织物来说最厚。
在这种情况下,发现织物密度一定、织物的浮长达到一定程度时,经纬纱受到交织点的控制几乎为零。此时,织物的厚度将达到最大,约为经纬纱直径之和(d1+d2=0.498 mm,其中纬纱直径 d1=0.323 mm;经纱直径 d2=0.175 mm)。此时,即使浮长增加,织物的厚度也不再变化。为此另外设计了八枚缎与十二枚缎进行了验证分析。
2.2 曲线拟合分析
针对经纱与纬纱交织,不同组织产生的不等浮长线与厚度的测试结果,采用曲线拟合的方法分析浮长对织物厚度的影响。假设交织处经纬纱直径为一个单位长度1,则自变量x的一个交织点所控制的经纱或纬纱到下一个交织点的纱线浮长则为2,同理可知平纹浮长横跨点数为斜纹横跨点数为3,斜纹横跨点数为4,五枚缎纹横跨点数为5,八枚缎纹横跨点数为8,十二枚缎纹横跨点数为12。曲线拟合如图4所示,拟合方程如下式所示,其中R2=0.9914。
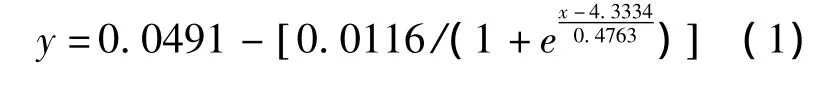
织物厚度为应变量y。可以看出该曲线类似于S形态。在浮长线长度L小于等于5时,曲线近似于一条平直的斜线,此时厚度与浮长呈正比关系。当织物浮长长度L大于8以后,织物厚度曲线趋于平缓,甚至不再变化。这是因为经纬纱受交叉点影响较小,纱线压扁系数较大,织物厚度趋于经纬纱直径之和,不再变化。
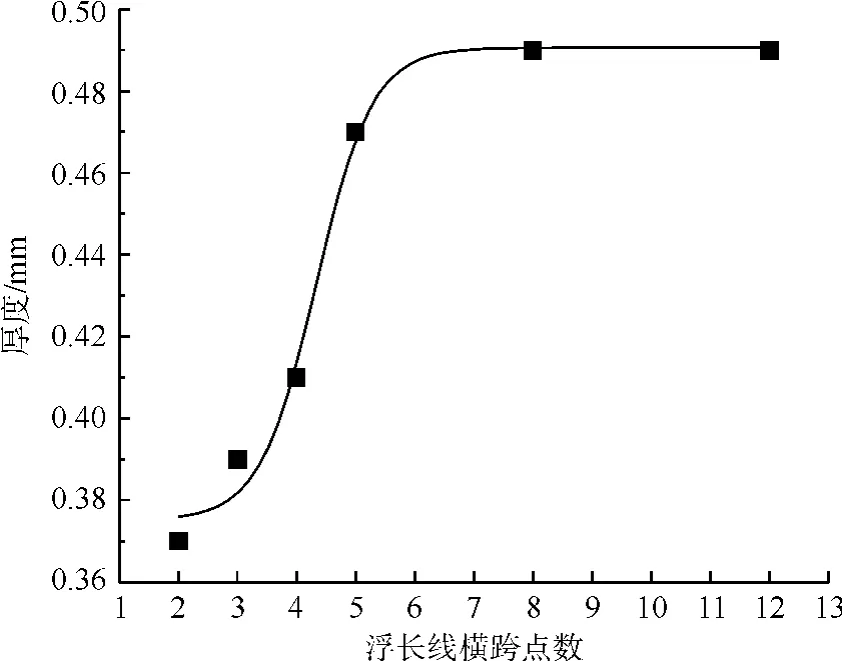
图4 织物浮长与厚度关系Fig.4 Relationship between fabric floating length and thickness
3 结果与讨论
织物的组织结构与织物的厚度有着直接的影响。这是由于组织结构造成的浮长线的长短不同,浮长线长时就会很难得到交织点的控制,纱线截面趋于圆形,横跨于织物表层,因此织物较厚;浮长线短时,经纬纱受到有效控制,纱线因交叉压力而变得趋于扁平,织物厚度较小。在织物密度相同情况下,织物浮长受到有效控制时,织物厚度与浮长趋于正比关系。
[1]陈辉,沈毅,刘玄木,等.织物厚度与悬垂性能的回归分析[J].浙江理工大学学报,2005,22(2):110-113.CHEN Hui,SHEN Yi,LIU Xuanmu,et al.Linear regression of fabric's thickness versus drape behavior[J].Journal of Zhejiang Sci-Tech Univeristy,2005,22(2):110-113.
[2]陈香云,吴薇.不同季节服用织物热湿舒适性能评价体系[J].现代纺织技术,2012,20(1):46-48.CHEN Xiangyun,WU Wei.Appraisal system of hot-wet comfortable properties for garment fabric in different seasons[J].Advanced Textile Technology,2012,20(1):46-48.
[3]蒋艳凤,翁毅.织物厚度测试中的影响因素探讨[J].现代纺织技术,2000,8(3):40-41.JIANG Yanfeng,WENG Yi.Influence factors disscussion on the fabric thickness test[J].Advanced Textile Technology,2000,8(3):40-41.
[4]郑天勇.纺织品CAD/CAM[M].北京:化学工业出版社,2007:155-176.ZHENG Tianyong.CAD/CAM for Texitle[M].Beijing:Chemical Industry Press,2007:155-176.
[5]顾平.织物组织与结构学[M].上海:东华大学出版社,2009:201-206.GU Ping,Fabric Weaves and Structures[M].Shanghai:Donghua University Press,2009:201-206.
[6]蔡雨,郑天勇,景书娟,等.Peirce平纹机织物结构模型的计算精确度[J].纺织学报,2012,33(1):48-53.CAI Yu,ZHENGTianyong,JING Shujuan,et al.Calculated accuracy of Peirce's plain woven fabric model for geometric structure of plain woven fabrics[J].Journal of Textile Research,2012,33(1):48-53.
[7]邢连华.纱线在织物的屈曲和织物厚度[J].天津纺织工学院学报,1990,9(3):19-25.XING Lianhua.The yarn crimp in fabric anb its thickness[J].Tianjin Textile Institute of Technology,1990,9(3):19-25.
[8]朱美男,费万春.织物厚度指标的探讨[J].丝绸,2002(12):42-43.ZHU Meinan,FEI Wanchun.Disscussion on the fabric thickness index[J].Journal of Silk,2002(12):42-43.

