DDA直线插补在ARM中的设计与实现
王彦,肖铁红
(1.武汉铁路职业技术学院,湖北 武汉 430205;2.大唐耒阳发电厂信息中心,湖南 耒阳 421800)
0 引言
数控车床、数控雕刻机均是步进电机为驱动器件的开环控制系统,均采用全数字化的控制方案.多轴运动一般采用数字积分法DDA(digital differential analyzer)插补方式实现,而DDA插补的实现往往需要很大的计算量,一般采用X86计算机+运动控制卡实现,但其功耗、便携性、成本有很大的局限性.随着计算机技术的发展,ARM技术使功耗、成本、性能有了较大的改进,因此,在ARM平台上实现DDA插补技术和步进电机控制,对通用数控平台(数控雕刻机、数控车床等)的市场竞争力有很大的提高.本文中以四轴插补为例,通过对DDA插补的分析,综合运用数学、计算机知识,对在ARM平台上实现多轴DDA插补做了详细的研究.
1 四轴DDA直线插补原理
被控对象的运动轨迹由各种线型构成,如直线、圆弧、抛物线等,其中最主要的是直线和圆弧.为了实现轨迹控制,必须进行插补,计算出中间点,插补的任务就是从轨迹起点到终点之间的数据密化工作.DDA插补是一种常用的解决多轴联动的方案.

其中:K为比例常数.
刀具在x,y,z,u方向上移动的微小增量分别为:
从起点到终点的过程,是每一个坐标轴每一个单位时间间隔Δt分别同时累加的过程,经过n(nK=1)次累加后,x,y,z,u均分别到终点,本次插补过程结束[1].即
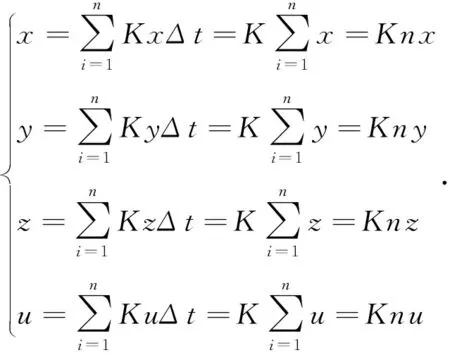
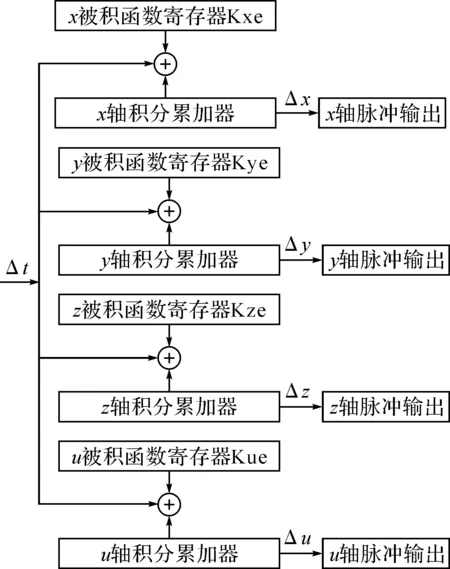
图1 四轴DDA插补流程图
1.2四轴DDA直线插补的计算机实现流程对于二进制运算的计算机,根据其特点,取K=1/2m,则累加次数n=1/K=2m,把x左移m位,由于寄存器是m位的,所以它存放的Ax的数值和x是相同的,每个坐标的积分器由累加器和被积函数寄存器组成,被积函数寄存器中存放的是坐标的终点数值,Δt表示插补运算周期,每经过一个插补运算周期,被积函数的内容便相应地累加一次,被积函数的溢出作为驱动相应坐标轴的进给脉冲,而余数仍然存放在被积函数中作为继续积分的初值[2].四轴DDA插补流程图如图1所示.
2 DDA插补中的加减速控制
在步进电机的开环控制系统中,加减速控制为连续控制中必不可少的环节.为了解决步进电机启停过程中的升降速运动变换带来的问题,必须通过对步进电机的进给脉冲频率进行加减,并且在步进电机的矩频特性曲线选择上保留一定的余量.加速时,保证进给脉冲频率逐渐增大;减速时,保证进给脉冲逐渐减小.
目前的数控系统中,常用的加减速算法有直线加减速控制算法和S曲线加减速控制算法等.
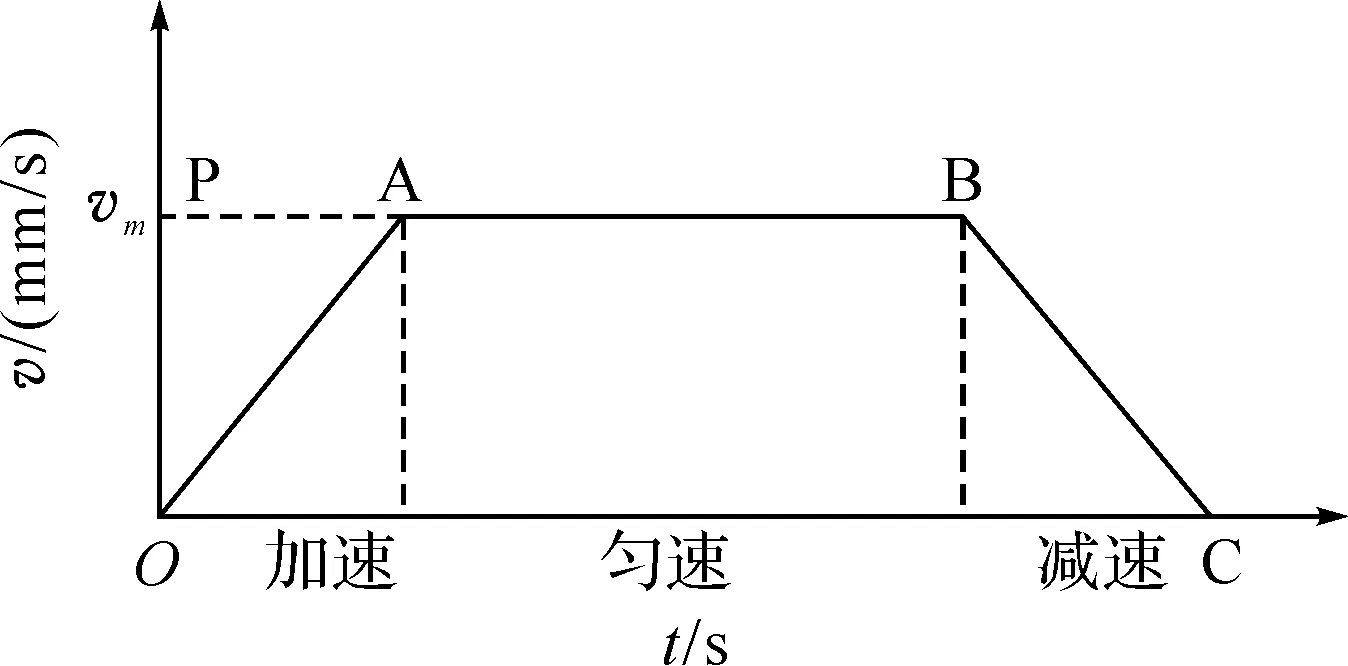
图2 梯形加减速控制曲线
2.1梯形加减速控制梯形加减速即步进电机启动时,其速度沿一定斜率的直线上升,停止时,其速度沿一定斜率的直线下降.梯形加减速控制曲线如图2所示.
由于直线的斜率一定,加减速的加速度恒定,所以实现所需要的计算量相对较小,消耗的资源也较少.缺点是没有充分考虑步进电机输出力矩随转速变化的特性,在高速情况下有可能发生失步.其加减速过程与匀速过程不能光滑地过渡切换,因此对机械可能有一定的冲击,适合用于处理速度较慢,对加减速要求不高的控制系统.

图3 指数加减速控制曲线
2.2指数加减速控制算法指数加减速曲线如图3所示.速度以加速和减速的方式进行,其加速和减速曲线对称.
下面研究加速阶段的指数运行曲线.运行速度公式为v(t)=vc(1-e-t/τ),其中vc代表终点速度或频率,t代表时间,τ代表调节系统时间常数[3].时间常数τ反映了系统从速度为0变化到给定的最高速度的变化效率,加速过程的时间受时间常数τ的约束,所以采用指数曲线进行加减速需根据系统选好的时间常数τ.将上式分解得:
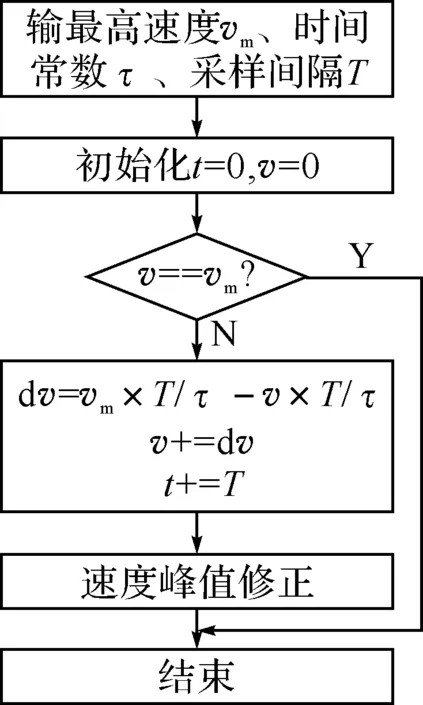
图4 产生指数加减速曲线流程图
由此得到第n步的速度或频率的进给Δv为:
Δv=v(nT)-v(n-1)nT=T/τ·vc-(T/τ)·(v(n-1)T)
因此只需给出每个采样时间间隔T内在速度或频率上需要的进给量,使算法实现了数字化.产生指数加减速曲线流程图如图4所示.
3 ARM中对可调速DDA插补算法的实现
嵌入式ARM控制器一般将操作系统和功能软件集成于系统硬件中,通常具有低功耗、体积小、集成度高等特点.因此其软件、算法均必须量体裁衣,去除冗余,力争以最低的功耗获取最高的性能.基于上述要求,并结合实际使用场合中对差补速度和精度的要求,本文中以STM32为ARM载体设计了精简的4轴DDA插补控制器.

图5 ARM实现梯形加减速的DDA插补流程图
3.1Coextend-M3系列ARM器件STM32的特点
STM32F103xx增强型系列使用高性能的ARM Cortex-M3 32位的RISC内核,工作频率为72 MHz,内置高速存储器(高达128 k字节的闪存和20 k字节的SRAM),丰富的增强I/O端口和联接到两条APB总线的外设.所有型号的器件都包含2个12位的ADC、3个通用16位定时器和一个PWM定时器,还包含标准和先进的通信接口,多达2个I2C和SPI、3个USART、一个USB和一个CAN.其较高的主频可以实现较高的插补脉冲输出,其丰富的外部接口又为驱动运动控制器所需要的LCD触摸屏、网络接口等提供了充分的条件.
3.2ARM中对可调速DDA插补的C语言实现在编写ARM的应用程序时,一般采用C或C++语言.针对核心的算法一般采用C语言实现.本文中对在ARM中实现可调速DDA直线插补的方法如下:分别将x,y,z,u的各个轴的驱动器的脉冲输出定义为相关引脚PIN_X,PIN_Y,PIN_Z,PIN_U,首先利用查找最大值算法找出x,y,z,u轴需要运动的最大轴,并判别各个轴的运动方向,其次根据设置的最大速度、最小速度和加速度在线计算出加速点、减速点,最后利用计算出的相关参数实现相应斜率的梯形加减速DDA插补运动,ARM实现梯形加减速的DDA插补流程图如图5所示[4].
3.3ARM方案相对X86方案的优势相比基于X86架构的PC机实现的数控插补,基于ARM实现的方案具有明显的优势.首先,PC机输出脉冲是基于软件延时实现的,但是受到操作系统自身线程切换和中断的影响,其精度无法保证,一般基于X86机实现的DDA插补只能实现50 kHz左右脉冲的输出,而基于ARM实现的脉冲输出可达200 kHz以上.其次,使用基于X86架构的PC,一般体积比较庞大,功耗非常高,在很多场合使用不方便.基于ARM的运动控制器件体积小、功耗低、扩展性强、开发灵活,不仅简化了电路,降低了成本,更重要的是提高了系统的整体性能.并且,随着电子工艺的发展,业界非常注重ARM芯片的外设的增强和性能的提高,使用ARM完成DDA插补的运动控制也是电子行业发展的方向.
4 结论
插补技术是数控系统的核心,简洁、高效的插补是ARM中实现插补算法的关键.本文中对数控技术中的关键算法(带速度控制的DDA插补算法)在ARM平台上的实现进行了完整的描述和分析,结合一种特定的ARM控制器STM32F103给出了实现的具体流程图,并针对大量使用的嵌入式系统进行了算法的优化,插补频率最高可达200 kHz,输出效果能够满足大多数现代高精度多轴联动的场合,具有较高的实用价值.
[1] 王爱玲.现代数控原理及控制系统[M].北京:国防工业出版社,2005:10-20.
[2] 游达章,苏旭武.两轴联动的数字积分算法的实现[J].装备制造技术,2008(1):41-43.
[3] Liang H, Hong H. A combined 3D linear and circular interpellation technique for multi-axis CNC machine[J]. Journal of Manufacturing Science and Engineering,2002,124(2):305-312.
[4] 彭彬彬,庞学慧,马天海.一种新型插补算法及其经济型数控系统中的应用[J].新技术新工艺,2001(11):4-5.

