基于蒙特卡罗有限元法分析运营中的厦门海底隧道荷载效应

尹蓉蓉

(1.同济大学 地下建筑与工程系,上海 200092)(2.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)

对工程结构进行可靠度分析时,通常采用R-S模式[1-5],即将广义作用效应S和广义抗力R视为基本随机变量,因而对作用效应S的概率特性分析必不可少.作用效应可通过结构分析得到,传统的结构分析有解析法和数值分析法.对于大型或复杂结构,通常用数值分析法——有限单元法.传统的有限元进行隧道结构分析时,认为材料性能、几何参数、边界条件及荷载等都是确定的.这种确定性分析忽视客观存在的各参数的离散性和变异性,不能科学地反映隧道的实际状况,满足不了可靠度分析的要求.隧道是大型的、复杂的随机结构,其荷载效应必须采用有效的随机数值方法进行分析,文中采用的随机数值方法为蒙特卡罗有限元法.

1 蒙特卡罗有限元法

蒙特卡罗和有限元的结合称为蒙特卡罗有限元法,该法通过在计算机上随机抽样产生的样本函数来模拟系统输入量的概率特性,并在每个给定的样本点,对系统进行确定的有限元分析,从而得到系统的随机响应量的概率特征[6].

用蒙特卡罗有限元法分析作用效应的概率特征的步骤如下:

1)首先用随机抽样法对影响可靠性的随机变量进行大量随机抽样,产生一系列均匀、独立分布的随机数,然后通过变换求得适合各随机变量分布规律的系列随机数,于是每一变量都有相应的一组随机数,每一组随机数的个数就是取样数;

2)将各个随机变量的随机数逐一代入有限元控制方程并求解,得到一组作用效应的解;

3)将这组作用效应的解进行统计分析,得到作用效应的概率特性.

2 运营公路隧道荷载效应

2.1 运营公路隧道荷载特点

对运营公路隧道进行可靠性评估时,必须先分析荷载的概率模型和统计参数.由于车辆荷载及其冲击荷载、人群荷载等可变荷载对公路隧道产生的影响较小,因此,隧道衬砌所承受的荷载主要考虑恒荷载.目前,对恒荷载的概率模型及统计参数的研究大都是针对拟建隧道而言,对于已建隧道,其荷载具有自身的特殊性,因此,在已建隧道的可靠性评估中,仍然按照结构设计的荷载规范来确定荷载值的方法显然存在不合理性,应进一步研究其荷载特性.概括起来,这些特殊性主要表现在以下几个方面:

1)隧道设计过程采用荷载概率模型和统计参数具有一般性和普遍性,已建隧道结构己成为一个客观实体,其作用环境更为具体化,其荷载概率模型和统计参数有自身特点;

2)隧道设计过程的荷载分析大都只能利用非自身的荷载信息,这些信息均属于隧道结构建成投入使用之前的信息,从某种意义上说只能算是对隧道在未来运营期内荷载的一种估计和预测.而已建隧道结构的荷载分析则可以建立在其自身的荷载信息基础上,即可以充分利用隧道在使用过程中产生的大量信息以及通过检测、试验手段获得的信息;

3)对于已建隧道,它的安全性与其现有状况、使用者的要求等有关,因此与设计可靠度分析有不同的特点,应根据具体情况取定.

2.2 影响公路隧道荷载效应的因素

从理论上说,运营公路隧道结构的荷载可以通过现场检测综合确定.但是,由于客观条件的限制,难以获得足够的数据,因而不能精确求得荷载的概率模型及统计参数.因此,可以在原有统计信息的基础上,利用运营公路隧道自身的荷载信息,对荷载特性进行修正,使其更接近实际.影响运营公路隧道荷载效应的因素包括:

1)荷载

①隧道衬砌竖向荷载取决于围岩塌方高度和围岩容重[7],根据日本松尾埝对围岩的统计结果:围岩容重γH的变异系数比围岩塌方高度H的变异系数整整小一个数量级,因此在计算中忽略其变异性,视为常量,其取值采用规范给出的中间值.②将垂直均布压力乘以不大于1.0的系数K0即为水平均布压力.其均值可按现行公路隧道规范[7]有关公式计算,变异系数为0.07.③围岩弹性抗力系数Kr的分布也服从正态分布[8].

2)衬砌性能不确定性

隧道衬砌的性能主要通过混凝土的弹性模量来反映,衬砌混凝土弹性模量一般都服从正态分布[9].

3)隧道衬砌厚度

衬砌厚度的变异性随设计厚度的减小而加大,衬砌厚度的均值一般可取原标准图设计厚度,变异系数对不同围岩取不同范围,一般可取0.1,0.15,0.2进行试算,分布类型为正态分布.

3 工程实例

3.1 工程概况

厦门翔安隧道起点位于厦门岛下边村南侧,西接城市干道仙丘路,从五通码头以北,沿北偏东约39°方向跨海,至同安岸下店村东北角,接大陆岸连接线,与福厦高速公路连接.

隧道全长8.695 km,其中海底隧道长6.05 km,跨越海域宽约4 200 m,按双向六车道高等级公路标准设计,是国内第一条海底隧道.设计采用三孔隧道方案,两侧为行车主洞,各设置3车道,行车主洞净宽13.5 m,净高5 m,建筑内轮廓面积122 m2.中孔为服务隧道,隧道中心线间距约60～80 m.

3.2 荷载效应计算

文中采用ANSYS有限元软件建立模型,运用PDS模块中的蒙特卡罗法进行可靠度分析,按荷载-结构模式计算.

1)行车隧道建筑限界及断面

行车隧道建筑限界净宽为13.50 m,净高为5.0 m,内侧设检修道.针对本隧道为3车道大断面的特点,隧道断面采用R-740 cm和R-570 cm的三心圆形式(图1).

2)材料物理力学参数和荷载计算

①材料物理力学性质

对于行车隧道,二次衬砌需采用钢筋混凝土结构,衬砌结构的类型和支护参数见表1.围岩、初期支护和二次衬砌的物理力学参数见表2.

表1 行车隧道计算截面复合式衬砌结构支护参数Table 1 Supporting parameters of composite lining of vehicular tunnel section

表2 材料物理力学参数Table 2 Physical and mechanical parameters of materials

②荷载计算

文中选择厦门海底隧道海域Ⅲ级(Ⅳ类)围岩下左洞某断面进行计算.在Ⅲ级(Ⅳ类)围岩地段,作用在二次衬砌上的荷载,按70%的围岩压力和全部静水压力考虑,剩余30%的围岩压力由初期支护和围岩共同组成的复合承载结构承担.静水压力按照隧道埋置深度进行调整,拱顶最大静水压力按0.65 MPa取值.上部土压力覆土荷载为隧道埋深与围岩容重的乘积,二衬所承受的水平荷载为152 kN·m-2,竖向荷载为760 kN·m-2.

3)有限元模型的建立

考虑本隧道衬砌仰拱不铺设防水板,仰拱与初期支护(围岩)有很好的粘结力,在静水压力下存在一定的拉抗力,计算中用均布弹簧进行模拟围岩与衬砌的相互作用.采用Combin14单元模拟弹簧,弹簧的弹性抗力系数见表2;采用Beam3单元模拟二衬.运用ANSYS软件进行有限元计算时,衬砌单元数为45,弹簧单元数为45,单元网格见图2.

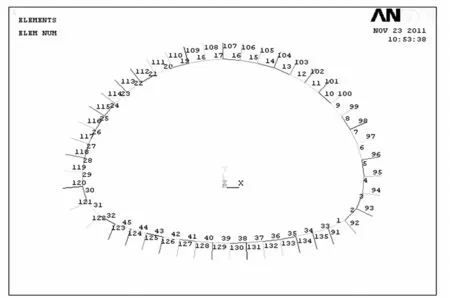
图2 单元网格Fig.2 Element mesh chart

3.3 计算荷载效应和轴力的特征分布

1)有限元计算结果

通过计算可得厦门海底隧计算断面衬砌的弯矩和轴力如图3,图中显示,二次衬砌结构在拱顶部位受拉,在拱脚部位受压,最大弯矩发生在拱脚部位.

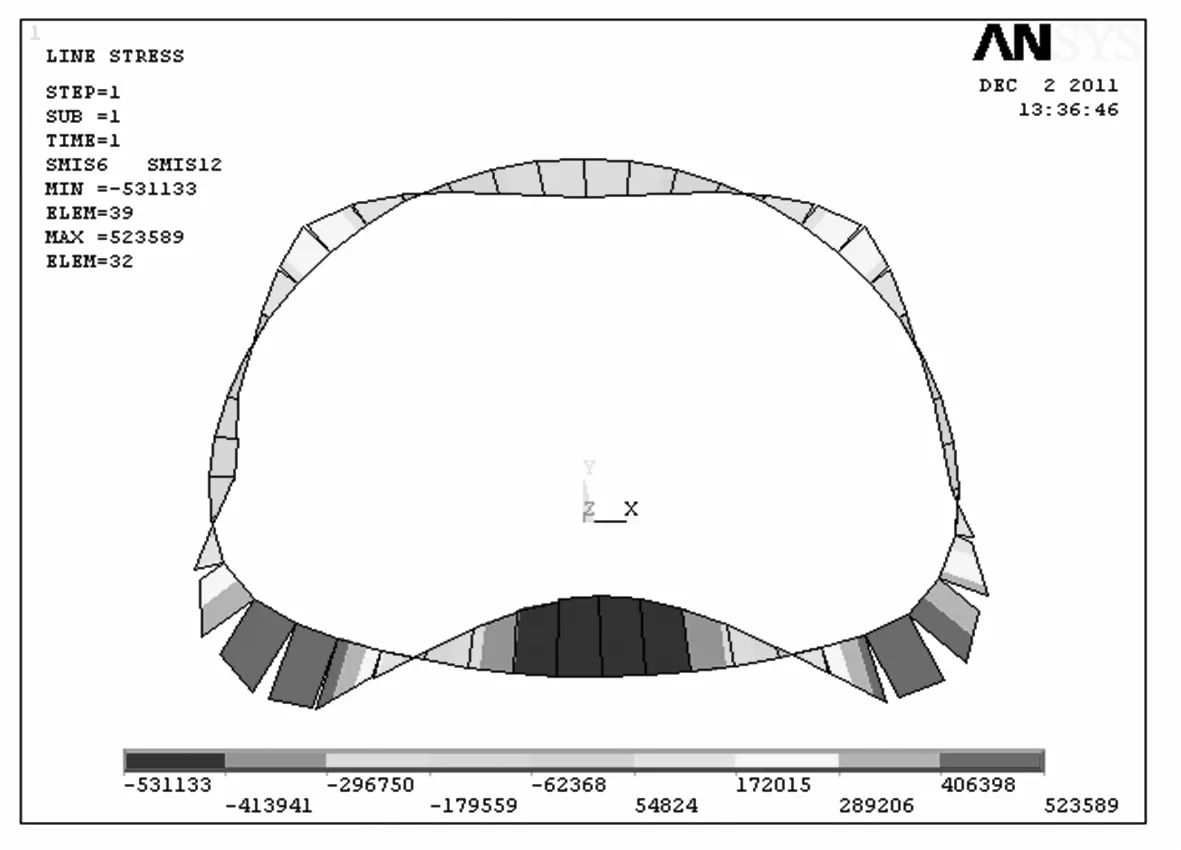
a) 弯矩

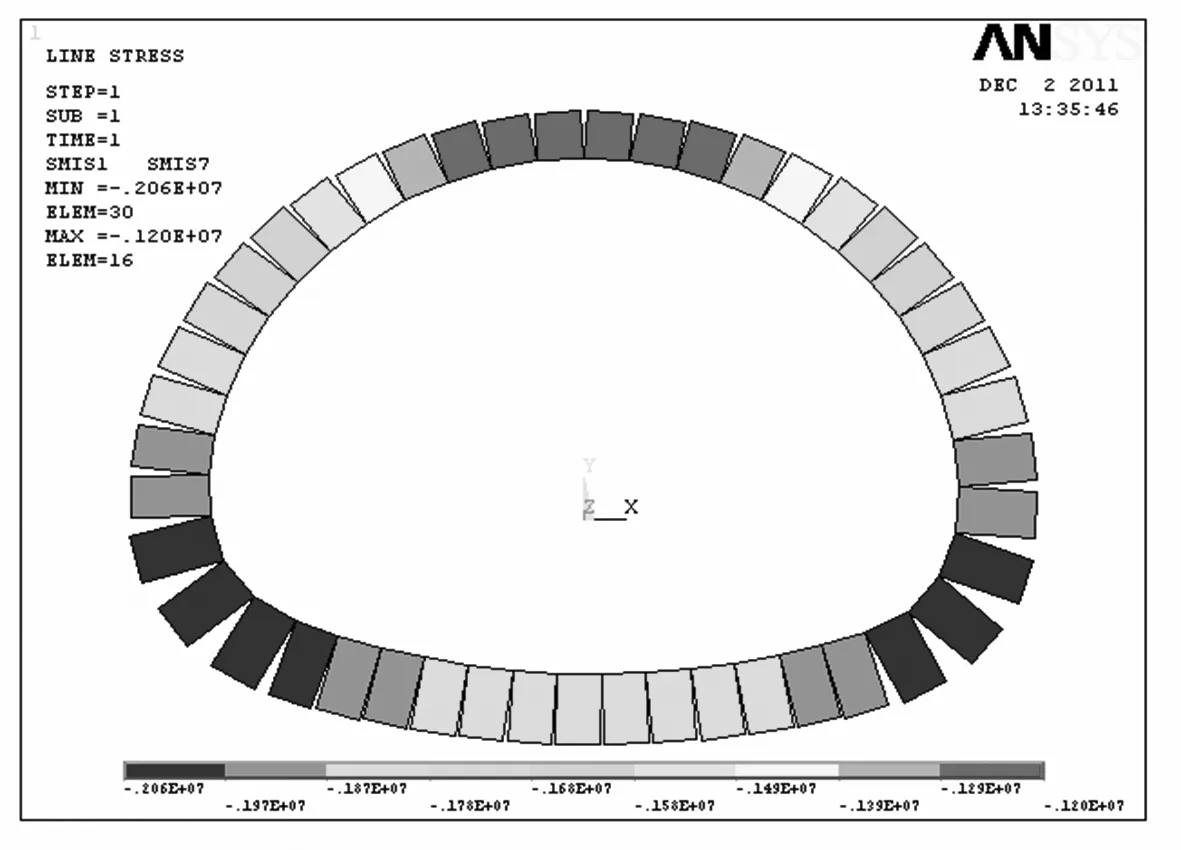
b)轴力

图3弯矩和轴力
Fig.3Bendingmomentandaxialforcediagram

2)各随机变量统计特征值

参照以往的研究成果,并按照本工程实例情况,各随机变量统计特征值列于表3中.

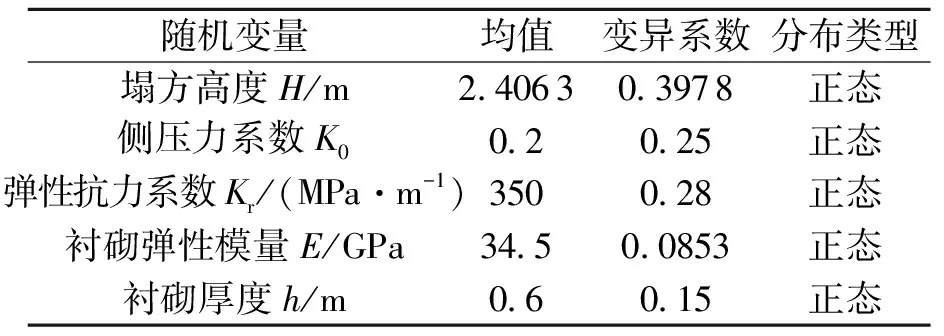
表3 随机变量的统计特征Table 3 Statistical characteristics of the random variable

3)计算结果

①弯矩的直方图和统计特征

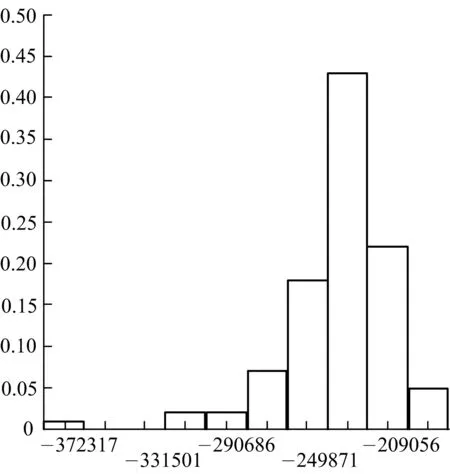
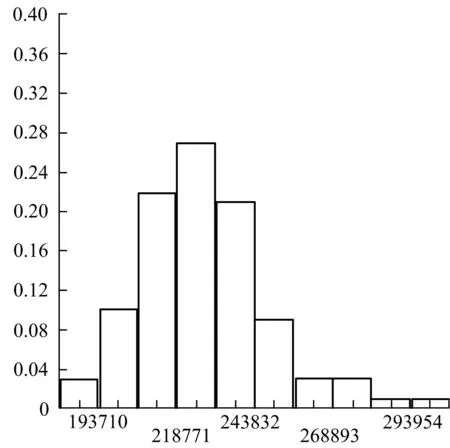
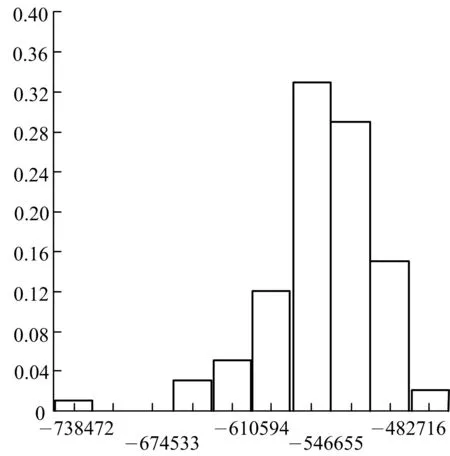
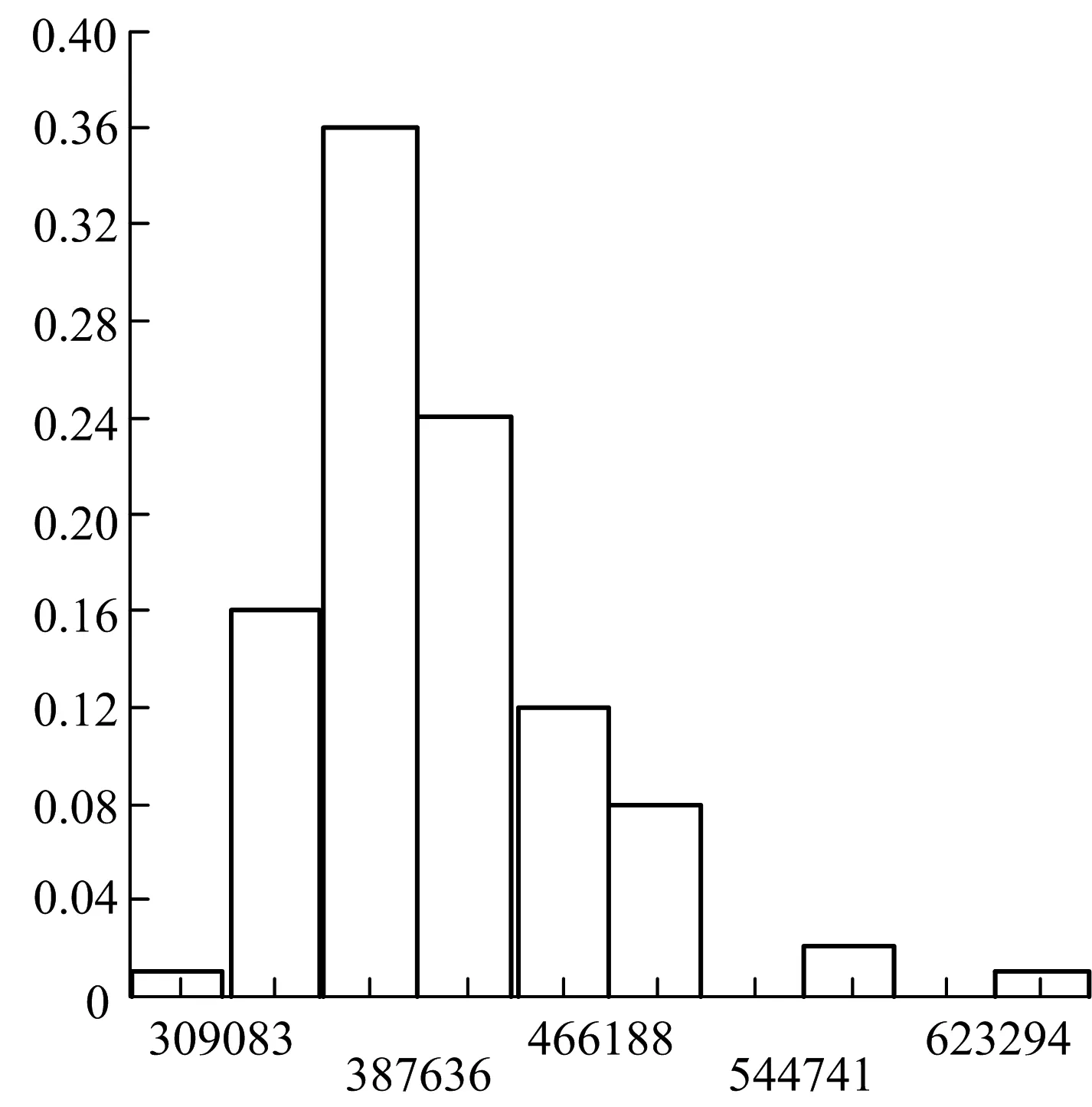
通过计算,可得厦门海底隧道计算断面衬砌拱顶(16号单元)、拱腰(11号单元)、最大弯矩(39号单元)以及最大轴力(30号单元)处的弯矩直方图(图4).

a) 衬砌拱顶处

b) 衬砌拱腰处

c) 衬砌最大弯矩处

d) 衬砌最大轴力处

确定荷载效应分布类型需要根据衬砌拱顶,拱腰、最大弯矩以及最大轴力处的弯矩的直方图,分别对其分布作出一种假设H0,然后进行假设检验.采用χ2检验法进行假设检验,可得衬砌拱顶处、拱腰、最大弯矩以及最大轴力处的弯矩不拒绝服从对数正态分布,统计特征值见表4.

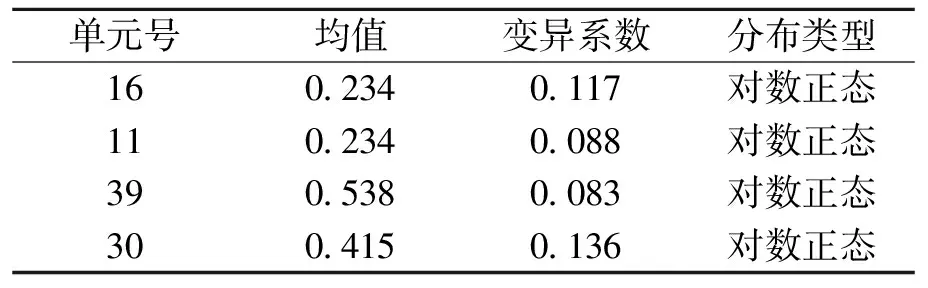
表4 弯矩的统计特征值Table 4 Statistical characteristic values of bending moments

②轴力直方图

通过计算,可得厦门海底隧道海域Ⅲ级(Ⅳ类)围岩下左洞某断面衬砌拱顶(16号单元)、拱腰(11号单元)、最大弯矩(39号单元)以及最大轴力(30号单元)处的轴力直方图(图5).

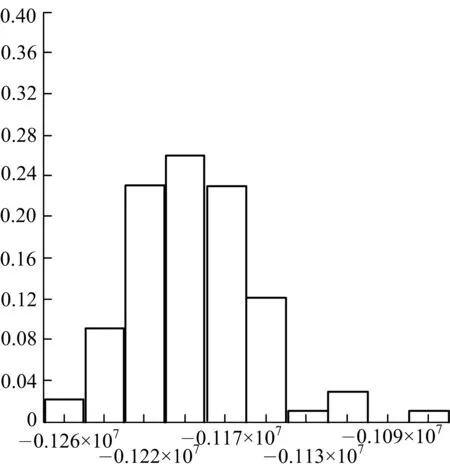
a) 衬砌拱顶处

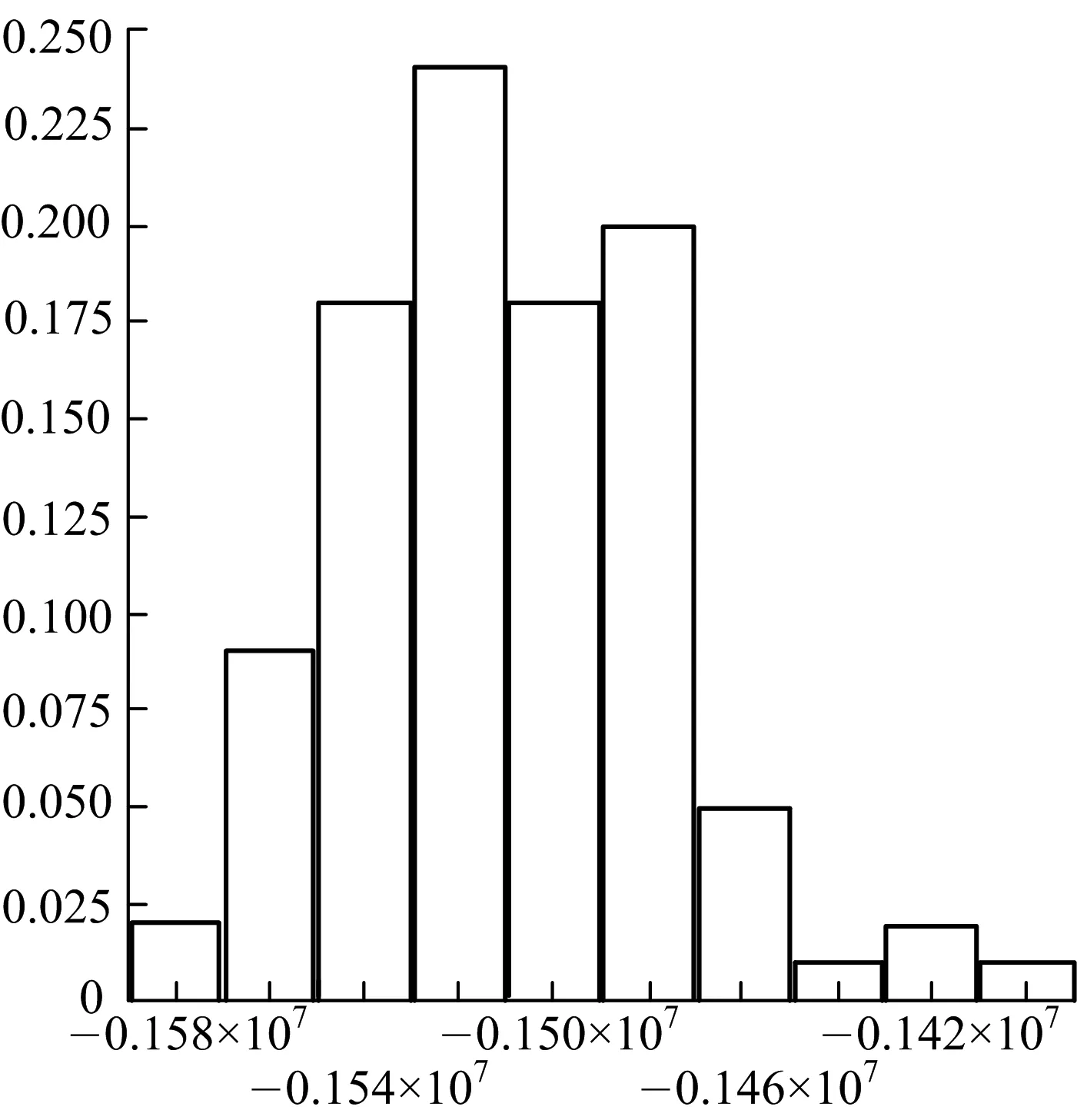
b) 衬砌拱腰处

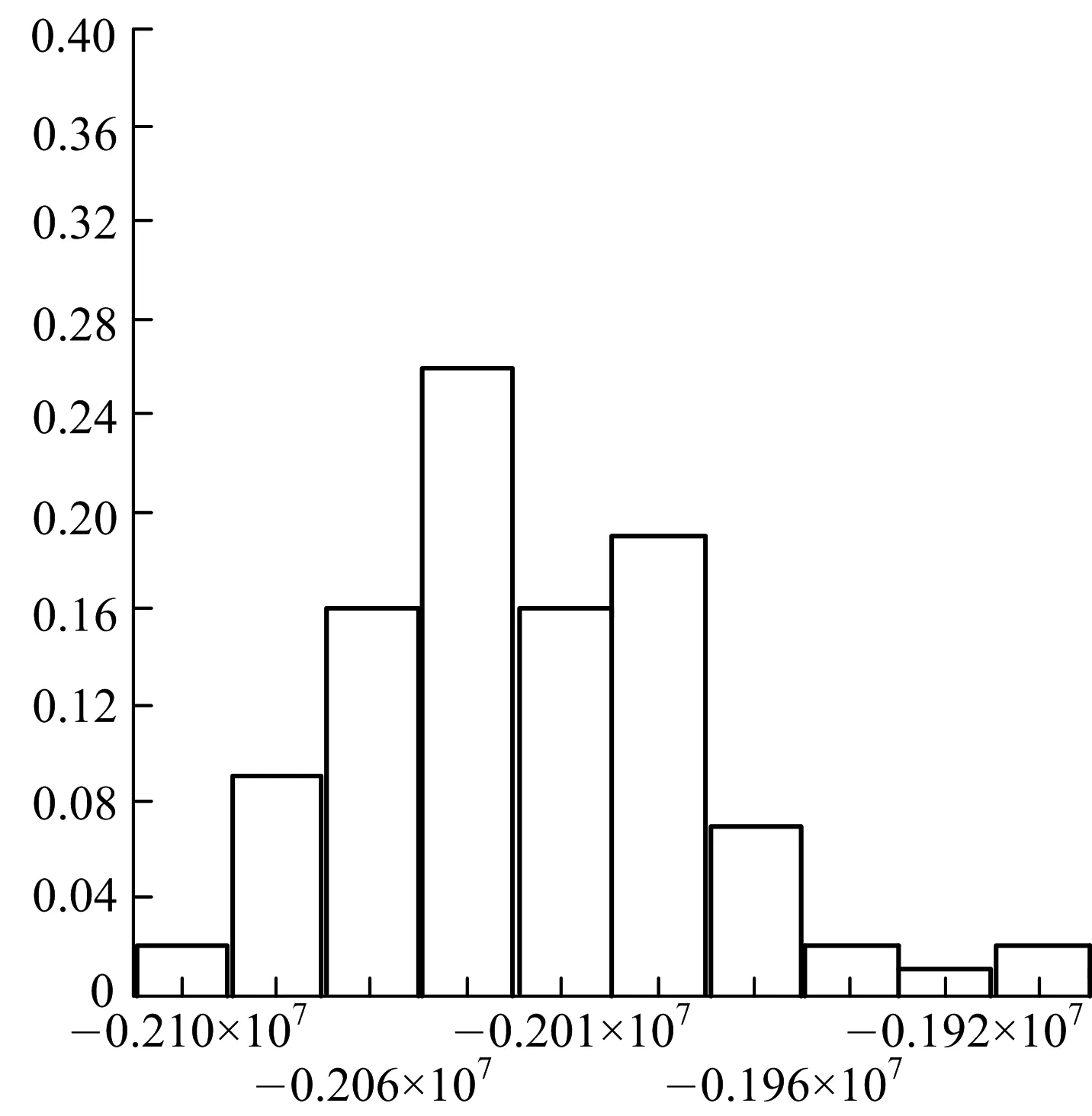
c) 衬砌最大轴力处

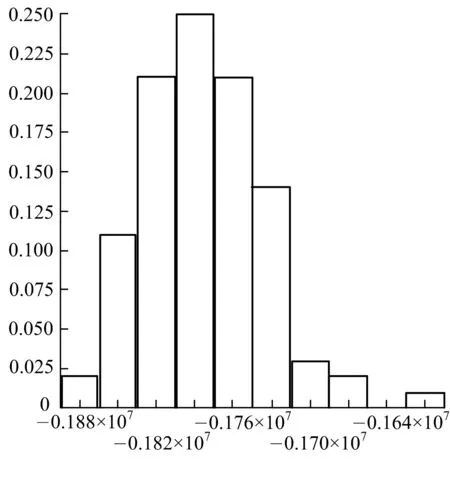
d) 衬砌最大弯矩处

通过假设检验,可得衬砌拱顶处、拱腰、最大弯矩以及最大轴力处的轴力不拒绝服从正态分布,统计特征值见表5.

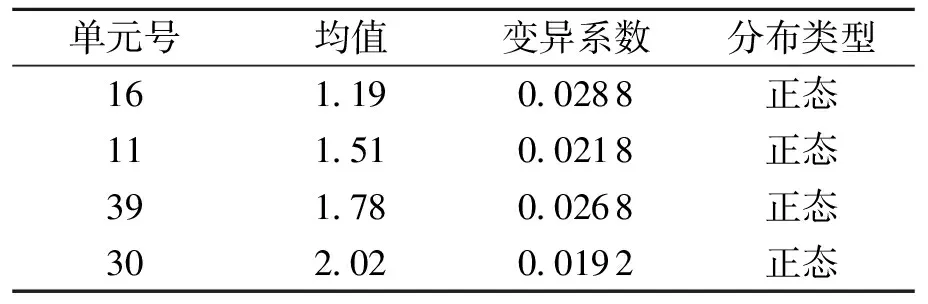
表5 轴力的统计特征值Table 5 Statistical characteristic values of axial force

4 结论

荷载效应分析是隧道安全性、可靠性评估的重要组成部分.文中运用蒙特卡罗有限元法对厦门海底隧道海域Ⅳ类围岩下左洞某断面二次衬砌的荷载效应和弯矩的统计特征进行了计算和分析,得出如下结论:

1)厦门海底隧道计算断面的二次衬砌结构最大弯矩发生在仰拱处,最大轴力发生在拱脚处;

2)由于公路隧道在拱顶和拱腰处易发生病害,所以文中计算了拱顶和拱腰处的弯矩和荷载效应的统计特征值;

3)根据可靠度分析可看出,衬砌拱顶、拱腰、拱脚及仰拱处的弯矩不拒绝服从对数正态分布;

4)衬砌拱顶、拱腰、拱脚和仰拱处的轴力即荷载效应不拒绝服从正态分布.

[1] Ang A H S，Tang W H.Probability concepts in engineering planing and design:Vol.l[M].New York:John Wiley & Sons,1975.

[2] Fiessler B,Rackwitz R,Neumann H J.Quadratic limit states in structural reliability[J].JournaloftheEngineeringMechanicsDivision,ASCE,1979,105(4):298-305.

[3] Tvedt L.The distribution of quadratic forms in normal space:an application to structural reliability[J].JournalofEngineeringMechanics,1990,116(6):531-538.

[4] Kiureghian A D,Lin H Z,Hwang S J.Second-order reliability approximation[J].JournalofEngineeringMechanics,1984,110(8):712-719.

[5] Cornell C A.Tructural safety specification based on second-moment reliability.Sym.Int.Assoc.ofBridgeandStruct.Engr.,London:1969.

[6] 景诗庭.隧道结构可靠度[M].北京:中国铁道出版社,2002.

[7] 中华人民共和国交通部.JTG D70-2004 公路隧道设计规范[S].北京:人民交通出版社,2004.

[8] 高谦.土木工程可靠性理论及其应用[M].北京:中国建材工业出版社,2007.

[9] 张清,王东元,李建军.铁路隧道衬砌结构可靠度分析[J].岩石力学与工程学报,1994,13(3):209-218.

Zhang Qing,Wang Dongyuan,Li Jianjiu.Reliability analysis of lining structures in chinese railroad tunnels[J].ChineseJournalofRockMechanicsandEngineering,1994,13(3):209-218.(in Chinese)