造船门式起重机模态分析研究
王 晟 李英春
(1.中船第九设计研究院工程有限公司,上海 200063;2.中国人民解放军第四八一零工厂,辽宁 116000)
1 进行模态分析的必要性
造船门式起重机作为船坞区分段合拢必不可少的起重设备,近几年有朝着超大跨度、超大起重量方向发展的趋势。在大型造船门式起重机(以下简称大型造船门机)结构的设计过程中,设计人员主要考虑的是结构的静强度、刚度和稳定性,忽视振动对整机结构的影响,其结果难免会使大型造船门机结构局部存在不合理之处。然而大型造船门机结构振动特性的优劣对其整体性能有着重要的影响,振动不仅可能会造成大型造船门机共振,而且造成其结构的疲劳破坏。当大型造船门机受到外界的载荷激励频率与其某一固有频率接近时,就有可能引起结构共振,从而产生很高的动应力,造成结构的强度破坏或产生不允许的大变形,破坏其使用性能。模态分析的作用主要是使结构避免共振或按特定频率进行振动。因此,对大型造船门机做模态分析是十分必要的。
本文以某船厂整机额定抬吊重量1 000 t,轨距145 m 的双梁大型造船门机为例,根据设计图纸建立ANSYS 模型,通过模态分析计算出其低阶的固有频率和振动阻尼,为结构设计人员提供相应的参考。
2 大型造船门机模态分析
2.1 模态分析理论基础
模态分析是所有动力学分析的基础,是确定结构或机器部件振动特性的一种技术。它可以计算出被分析结构的振动频率、振动型式以及阻尼,从而为金属结构设计人员提供信息,尽可能的避免一些特定频率下的振动。对于n 自由度的线性阻尼振动系统,其自由振动的运动微分方程为:
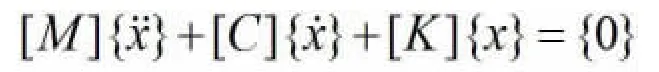
忽略阻尼不计,令[C]=0,即:
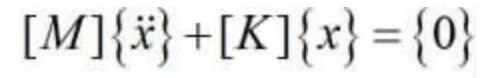
得到系统的特征方程为:
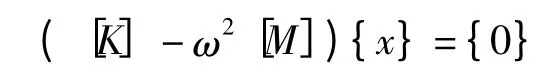
式中,ω 是系统固有频率。
2.2 大型造船门机有限元模型的建立
大型造船门机的主梁、刚性腿和柔性腿选用梁单元BEAM188,并根据其各部件的重量(考虑对应结构扶梯栏杆的重量)对每个部件的材料密度做适当的调整,以反映整机的质量大小和重心位置。对于在模型中无需建立但对整体质量分布有一定影响的部件,如上小车、下小车和维修吊等选用是集中质量单元MASS21。最终建立的ANSYS 模型如图1 所示。
2.3 施加约束
根据实际情况,主梁和刚性腿连接的位置采用刚性连接。主梁和柔性腿连接的位置采用铰接,将该连接位置的垂向自由度和沿大车轨道方向的自由度耦合,其它方向自由度释放。将该大型造船门机的大车运行机构简化为8 个相互连接的梁节点,并将8 个节点施加3 个方向的线位移约束。

图1 大型造船门机有限元模型Figure 1 Finite element model of heavy duty naval gantry crane
2.4 大型造船门机模态分析
由振动理论知识可知,高阶固有频率在结构存在阻尼的情况下迅速衰减,相对应的振动能量迅速减弱,在实际的振动过程中对结构的振动影响较小。在结构的振动过程中起主要作用的是较低阶振型所对应的固有频率。对于大型造船门机这样具有几十万个自由度的大型钢结构系统,利用模态分析计算其高阶固有频率和振型向量既费力、费时,又没有什么实际意义。因此对于大型钢结构系统,做模态分析一般都是选择前几阶的固有频率和振型作为研究对象。本文选择该大型造船门机的前10 阶固有频率和振型向量作为研究对象。通过ANSYS 的后处理结果,得到该大型造船门机前10 阶固有频率如表1 所示。
该大型造船门机前10 阶振型如图2~图11所示。
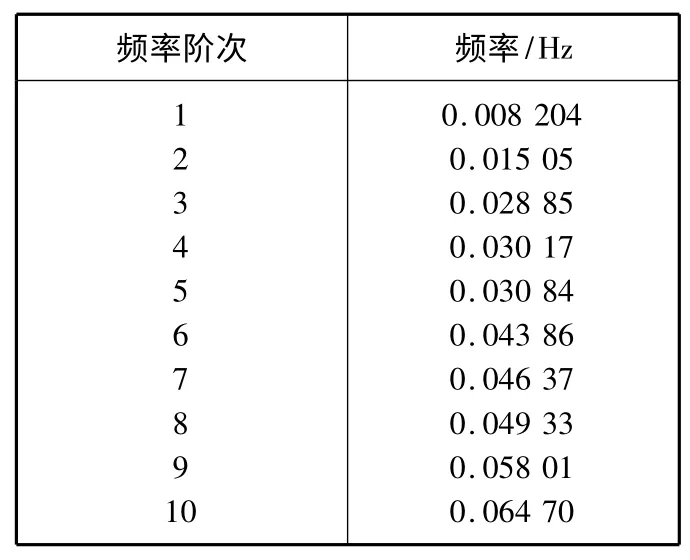
表1 该大型造船门机固有频率Table 1 Natural frequencies of the heavy duty naval gantry crane
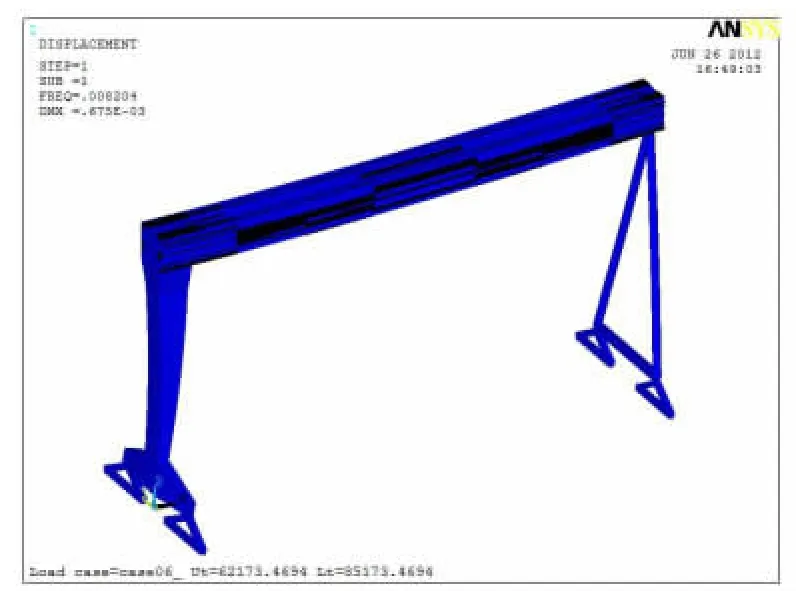
图2 第一阶振型Figure 1 1st phase vibration shape
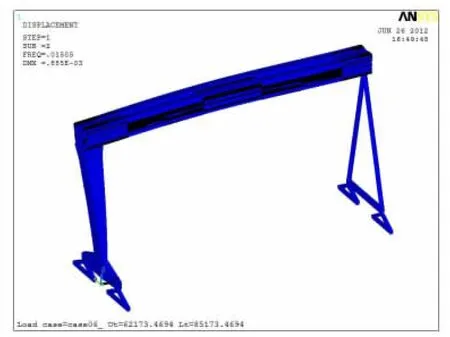
图3 第二阶振型Figure 3 2nd phase vibration shape
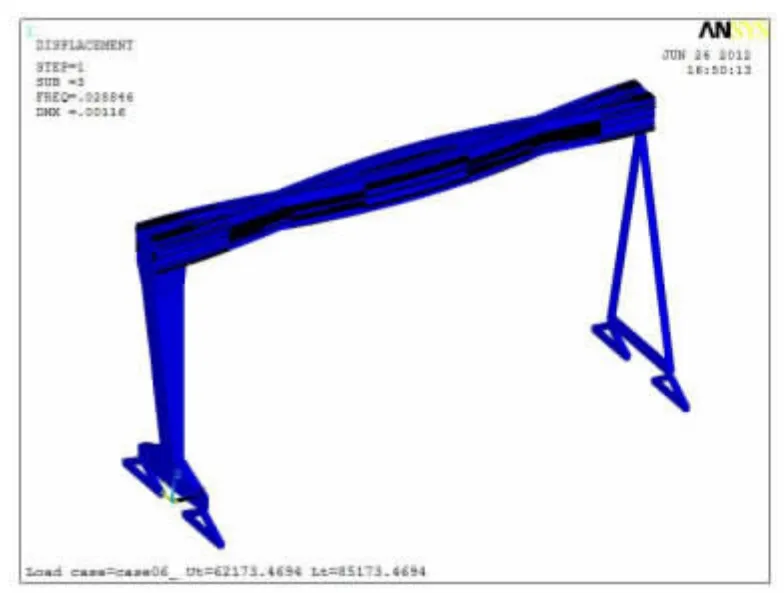
图4 第三阶振型Figure 4 3rd phase vibration shape

图5 第四阶振型Figure 5 4th phase vibration shape
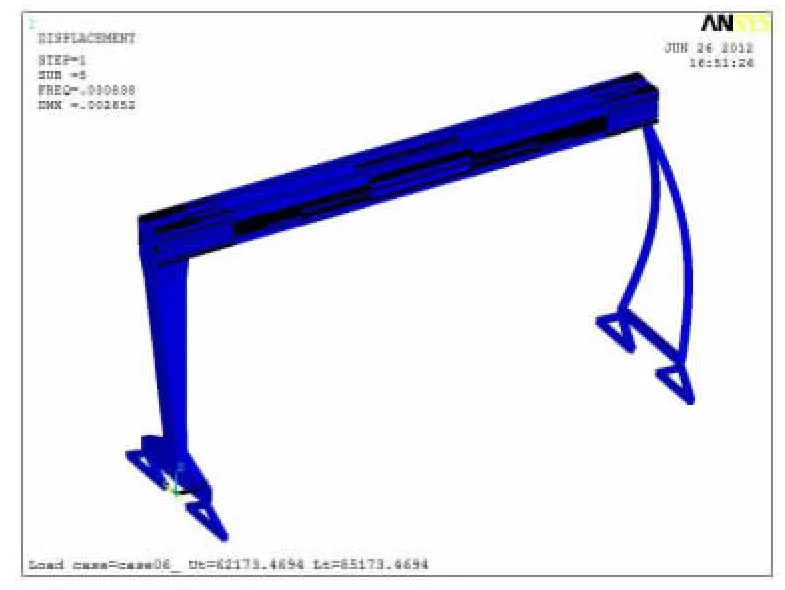
图6 第五阶振型Figure 6 5th phase vibration shape
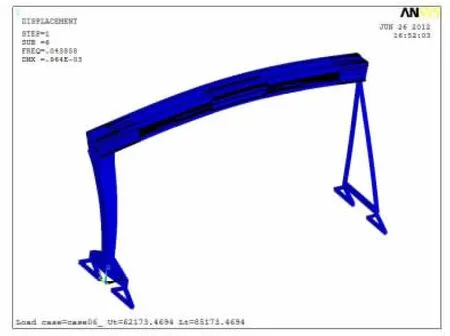
图7 第六阶振型Figure 7 6th phase vibration shape

图8 第七阶振型Figure 8 7th phase vibration shape
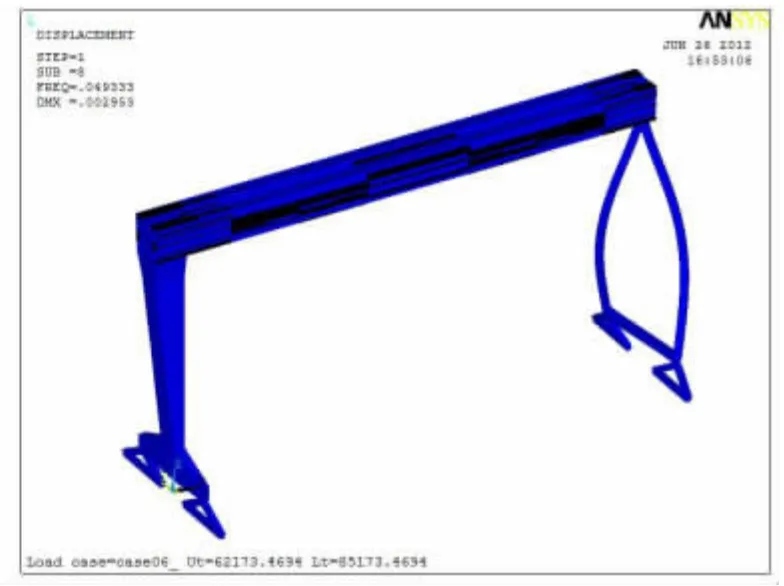
图9 第八阶振型Figure 9 8th phase vibration shape
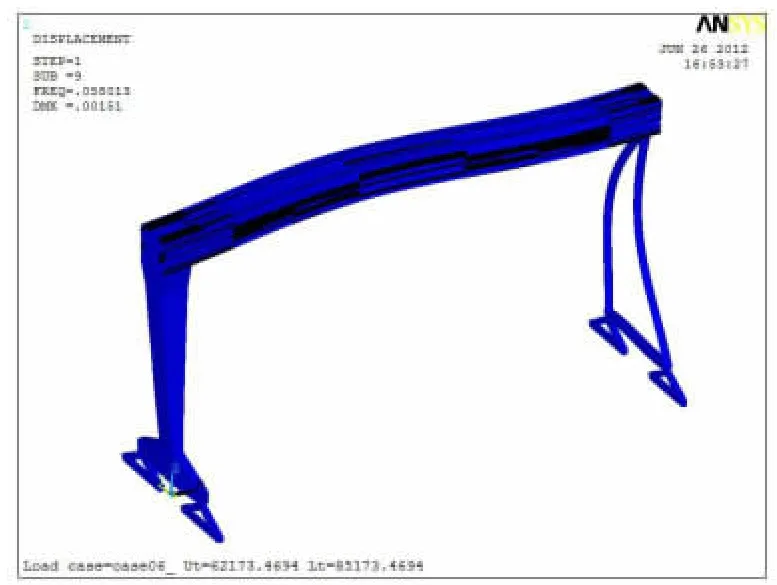
图10 第九阶振型Figure 10 9th phase vibration shape
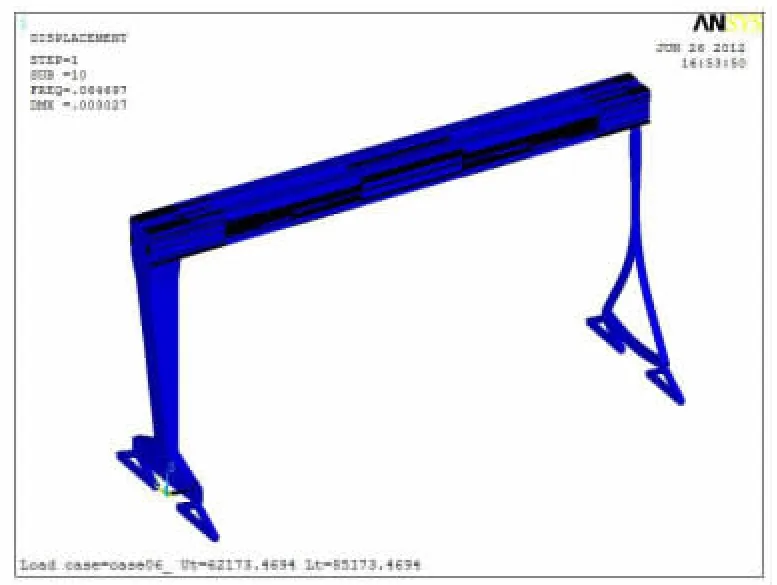
图11 第十阶振型Figure 11 10th phase vibration shape
由图2~图10 分析比较可得:前面第1 阶和第2 阶垂向振型不大,从第4 阶垂向振型向下达到最大值,到第6 阶垂向振型向上达到最大值。其余几阶振型主要是垂直于大车轨道和沿动车轨道方向,对整机的结构振动影响相对较小。因此选择表1 中第4 阶和第6 阶固有频率来计算该大型造船门机的阻尼系数。
2.5 船厂门式起重机阻尼计算
参考相关的文献,起重机金属结构一般阻尼比ξ=0.008~0.05,其中焊接结构取ξ=0.008~0.01,铆接结构取ξ=0.015~0.05,这些经验值为大型造船门机阻尼的计算提供了有益的帮助。根据该大型造船门机的工作特点,计算取阻尼比ξ=0.009。
根据对该大型造船门机起重机对结构影响较大的频率的上限和下限值,并选取合适的阻尼比ξ,计算出瑞利阻尼的两个重要系数Alpha(简称α)和Beta(简称β)值。瑞利阻尼的主要计算公式如下:
[C]=α[M]+β[K]
式中,[M]是质量矩阵;[M]是刚度矩阵。
系数α 和β 与阻尼比ξ 之间有如下关系:
α/(2ω)+βω/2=ξ
式中,ω=2πf,f 是频率,单位Hz。
对于固定的ξ 值,α 和β 随f 变化。确定选择f4和f6,通过联立方程来计算对应的α 和β,联立方程:
α/(2ω4)+βω6/2=ξ
α/(2ω4)+βω6/2=ξ
解为:
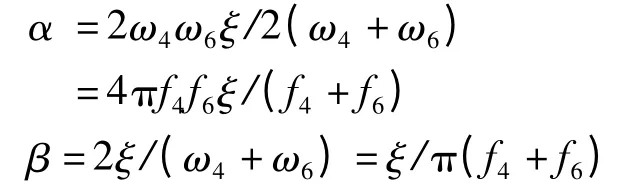
将表1 中的数据代入公式中可得α=1.01×10-3,β=3.87×10-2。
3 模态分析小结
(1)从表1 频率计算数值分析,该大型造船门机固有频率数值相当接近。这与该大型造船门机双梁呈对称结构相吻合,说明其模态分析计算结果是合理可信的。
(2)《起重机设计、使用和保养》中对大型造船门机固有频率要求应在f=0.7 Hz 范围内,以上计算结果满足该项要求,说明该起重机的设计满足固有频率的要求。
(3)通过计算发现α 和β 数值相对较小,说明大型造船门机的瑞利阻尼系数数值较小,衰减速度较慢,因此设计人员必须对小车运动方向的振动有足够的重视。
(4)通过计算发现α 和β 数值,发现α 数值远小于β 数值,说明在大型造船门机模态分析中,刚度对该种类型的起重机振动影响相对较大。
(5)从表1 的计算结果可知,大型造船门机振动频率小于2 Hz,属于低频振动。如此低的固有频率,意味着司机在作业时舒适度较差,建议在司机室或司机的座椅下增加隔振材料来提高作业的舒适性。
(6)使用单位应该尽量避免使用与表1 中相同或相近的外界激励,以免引起共振,对大型造船门机结构造成影响。
[1]胡宗武,阎以诵.起重机动力学.北京:机械工业出版社,1988.
[2]全国起重机机械标准化技术委员会.起重机设计规范.GB/T3811—2008.
[3]钱光浩.基于ANSYS 的龙门起重机门架结构动态设计与优化研究.武汉理工大学硕士学位论文,2008.
[4]王晟.海洋工况风浪载荷对浮式起重机结构影响分析研究.上海海事大学硕士论文.2009.
[5]Ing.J.Verschoof.起重机设计、使用和保养.上海:上海科学出版社,2002.
[6]王俊华,等.斗轮堆取料机在头部激振下的动态响应.起重运输机械,2012.

