从COBE数据推算早期宇宙实物密度的相对涨落
危 钰
(武汉铁路职业技术学院, 湖北 武汉 430205)
1 原子复合与光子退耦
宇宙早期处于极度高温状态,任何原子结构都不存在,宇宙各处无时无刻都发生着可逆反应:
e-+p↔H+γ
(1)
它的正向反应即原子的复合,为了研究复合和退耦的关系,做如下理论分析。
首先,把电离氢的数密度记作np,氢原子的数密度记作nH,于是可以定义气体的电离度为:
(2)
显然,在温度较高的时候电离度接近1,膨胀中温度降低使得电离度随之降低。在这个过程中还涉及到核子数和光子数之比的问题,把它们的比值记作:
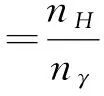
(3)
这个值往往是由观测事实来推定的, 值得注意的是,nH和nγ在宇宙膨胀中都与膨胀因子R3成反比,所以他们的比值η是不变的。下面为了讨论的继续,先暂时借用已有的数据,取η≈5×10-10.
令气体的温度为T,在统计平衡下,质子,电子和氢原子的量子涨落情况都满足Boltzmann分布,因此有:
(4)
(5)
(6)
式子中的μ代表各组分的化学势,m代表粒子静质量,g代表自旋自由度数。对于上述粒子我们已知:gp=ge=2 ,gH=4 ;mp+me-mH=B,另外考虑化学平衡和电中性条件有:
μp+μe=μH
(7)
np=ne
(8)
其中,已经利用光子组分化学势为零,且对于任意化学势为零的组分,其粒子数密度满足:
(9)
式子(9)中的上半部分针对波色组分,下半部分针对费米组分,且其中的ξ(3)≈1.202 是宗量为3的Riemannξ函数值。光子属于波色子,自旋自由度数为2,故由(9)可知光子的数密度为:
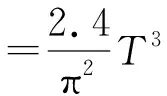
(10)
结合式子(3)和(10)可以有:
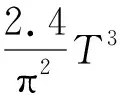
(11)
用式子(7)消去式子(4)(5)(6)中的化学势,再和式子(11)联立就能得到电离度Xp和温度T以及η之间的依赖关系了。把me和B这些粒子物理中的已知量带入,可以得到一个简单的数值结果:
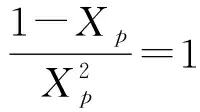
(12)
这里温度的单位为电子伏。由这个结果我们就能明确的看到,随着温度的降低,电离度大概在0.4eV到0.25eV之间连续而迅速的降低。
上面的推导只指出了电离度下降和温度之间的关系,但本质上,光子的退耦取决于光子和实物粒子的碰撞情况,也就是说,到底温度下降到什么程度可以认为上述复合反应不再继续,光子退出了与实物粒子复合的相互作用,这仍然需要从光子退耦的基本定义出发进一步分析。
在电离气体中,光子的热碰撞主要是和自由电子的Thomson散射,取自然单位制,则每个光子单位时间内的碰撞次数为:
Γ=neσTh
(13)
式中的σTh为散射截面,与光子能量无关,这个值在粒子物理中是清楚的,为:σTh=6.65×10-25cm2.
无论相互之间的关系多么复杂,宇宙膨胀是光子退耦的根本原因,膨胀用膨胀率H描写,可以从基本的宇宙动力学方程和宇宙模型的理论中推出,这些动力学方程包括Friedmann方程:
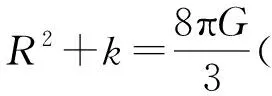
(14)
该方程是描述宇宙膨胀的基本方程,可以把常数项,曲率项和辐射项都忽略,得到:
(15)
下标0表示是今天的值,例如ρm0表示今天的实物密度。另外密度与宇宙尺度以及温度之间有关系:
(16)
式子(16)的后半部分利用了退耦后光子气体的等效温度满足RT=常数的结论,该结论在后面的讨论中会有证明。于是联立(15)和(16)并带入观测值:Hubble常数H0=65km·s-1·Mpc-1以及宇宙密度参量Ωm0=1/3 可以得到:
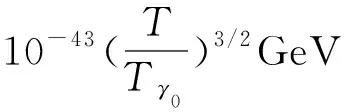
(17)
接下来讨论光子碰撞率随温度的变化,由于ne=np,式子(13)可以改写为:
Γ=XpηnγσTh
(18)
将式子(10)和散射截面代入式子(18),并用T/Tγ0代替 ,则得到:
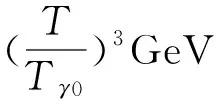
(19)
为简单起见,不妨取Γ=H作为光子退耦的标志,同时取η≈5×10-10,则联立式子(12)、(17)和(19)得出Xp≈4×10-3,相应的温度可以算出为Tdec=0.25eV,这就是光子退耦时的宇宙温度了。在COBE数据中可以看到这个理论计算与实际观测数据吻合的很好。
注意在上面的计算中,有许多宇宙学参数都直接取了观测值而未加讨论,并且认为是各向同性的。事实上,比较式子(17)和(19)可以看出,若令Γ=H为光子退耦的判据,那么如果我们测量到背景光子温度存在微弱的各向异性,则表示Xpη也存在着各向异性,也就是说,各方向上的电离度和核子光子数比有所不同,这就意味着各个方向上物质的密度可能存在差异,这种微弱的早期密度差异可能正是宇宙结构形成的起因。
2 COBE数据以及对早期密度涨落的推算
由美国国家航空宇航局(NASA)主持的宇宙背景辐射探测卫星(COBE)为我们提供了关于宇宙各向异性方面的数据,图1[1]是由Smoot教授领导的小组所作的实验观测图,他们为了比较各向上微弱的差异,对于全部的观测数据取对数,并计算了偏差,在图中,这种微弱的涨落被表现的非常直观。从观测数据上看,这种各向异性约为:δ=5×10-6.
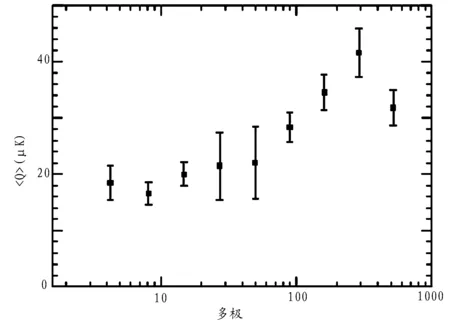
图1 图中对所有的观测数据取对数作为多极涨落的横坐标,并计算了它们的偏差。尽管这在统计上不是完备的,但可以展现各向异性。
首先,对于我们观测到的宇宙背景温度实际上是一个各个不同方向和空间的平均值,这个背景存在小的起伏,即T=T(θ,φ),对于这样的起伏用多极展开讨论比较方便,它的数学形式是按照球谐函数展开,即:
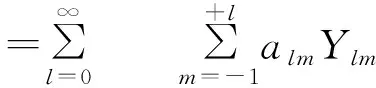
(20)
其中第一项a00是平均温度。第二项是偶极各向异性,它反映了观测者的运动速度。从第三项起,也就是四极各向异性才描述了退耦时的温度起伏(当然,事实上观测者运动的Doppler效应对高次项也有影响,扣除它们才是退耦时的起伏)。
多极起伏用δT描述,它与展开系数的关系是:
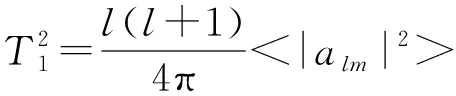
(21)
其中尖括号表示对m的平均,从结构形成的角度估算,δT1/T0约是μK数量级的。而COBE卫星上的一套仪器DMR在1992年测到了这个四极各向异性,它的大小是:
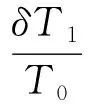
(22)
不妨取退耦时宇宙各向上的电离度为:Xp≈4×10-3,代入式子(12),可以得到:
17.6×10-14ηT3/2e13.6/T-0.996=0
(23)
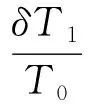
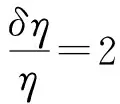
(24)
又由定义式(3)知道η是核子数与光子数之比,但在退耦时可以近似认为光子数是各向同性的,那么这个涨落就完全由核子数的涨落所决定,即:
δnH=nγδη
(25)
则相应引起的密度涨落应该为:
(26)
代入光子数密度,即得到密度相对涨落为:
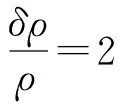
(27)
到此,我们就从背景辐射的涨落推导出了早期宇宙的实物密度涨落。
注意到实验数据中探测到的温度起伏是对10°范围内的天区扫描得到的平均值[1](仪器的分辨率只达到这个范围),也即是说,这个温度涨落对应着遥远宇宙中很大的一个区域。这个区域的大小表征了涨落的扰动尺度,光子退耦距现在的时间大约为tγ=1.37×1010年,则我们所观测到的天区距地球的距离大约为r=ctγ,所以这块天区的尺度应该为:
I=rθ=ctγθ≈3.6×1024m
(28)
则对应Jeans理论中扰动的波长为:
λ=2l=7.2×1024m
(29)
又已知Jeans自引力物质结团理论有临界结团波动尺度称之为Jeans尺度,它为:
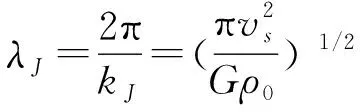
(30)
以式子(30)作为判据,代入必要的参量可以得出临界波长,其中声速的推算最为重要,因假设温度的微小变化不改变物态方程,即有:
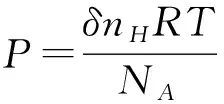
(31)
则声速应该为:
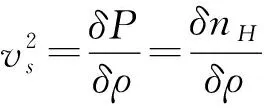
(32)
则临界波长为:
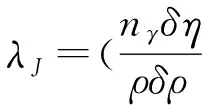
(33)
要求出现自引力不稳定性则要求波动的尺度不小于临界波长,即λ≥λJ,因此那个时候的宇宙密度临界值为:
ρ≥1.29×10-30kg·m-3
(34)
也就是说,退耦时宇宙的实物部分密度应该满足式子(34)才能出现自引力不稳定性从而导致结团。
3 分析与结论
据可靠观测数据,今天的宇宙实物密度大致的范围是:
ρ0≥4.7×10-28~3.6×10-27kg·m-3
(35)
退耦时刻的宇宙密度相对涨落以及在此涨落下满足自引力结团要求的临界密度值已经由式子(27)和(34)推算得到,对于为何与今天宇宙密度范围相差甚大的合理解释之一可能是在退耦时期的暗物质与普通物质的比例更大,也就是说也许暗物质正在逐步转化为可观测物质,又或者暗物质相对于可观测物质的占比正在减少。如果认为宇宙的变化一直是一个连续的没有阶段跃变的过程,那么可能越早期的宇宙中,暗物质所占的比例就越大。那么暗物质对于宇宙结构的形成可能起着更重要的作用。
当然,这些在很大程度上只是估算,毕竟这个涨落的分辨率为10度左右,把我们关心的更细致的起伏都抹去了。2001年升空的观测卫星MAP和2007年发射的卫星Planck Surveyor都准备在更高的分辨率下测量温度起伏,这些问题有待进一步的实验数据与分析。
参考文献:
[1]俞允强.物理宇宙学讲义[M].北京:北京大学出版社,2002.
[2]John A Peacock.Cosmological Physics[M].Cambridge: University Press, 1999.
[3]George F Smoot.COBE Observation and Results[J].arXiv:astro-ph/9902027v1 1 Feb 1999.
[4]Smoot G F, Scott D.Cosmic Microwave Background Mini-review[J].arXiv:astro-ph/0601307v1 14 Jan 2006.
[5]Smoot G F, Scott D.Cosmic Background Radiation[J].arXiv:astro-ph/9711069v1 8 Nov 1997.
[6]Smoot G F.CMB Synchrotron Foreground[J].arXiv:astro-ph/9902201v1 14 Feb 1999.
[7]Erminia Calabrese, Anˇze Slosar,Alessandro Melchiorri,et al. Cosmic Microwave Weak lensing data as a test for the dark universe[J].arXiv:astro-ph/08032309v1 17 Mar 2008.
[8]George F Smoot.Cosmic Microwave Background Radiation Anisotropies: their Discovery and Utilization[J].Rev Mod Phys,2007,79, 1349.
[9]Black C,Wall J.A velocity dipole in the distribution of radio galaxies[J].Nature,2002:416,6877:150~152.
[10]Coles Peter,Chiang.Lung-Yih.Characterizing,The nonlinear growth of large-scale structure in the Universe[J].Nature,2000,406,6794:376~378.
[11]Radek Stompor, Amedeo Balbi, Julian D Borrill,et al. Making maps of the cosmic microwave background: The MAXIMA example[J].Phys Rev, 2002,D 65, 022003.
[12]Richard L Davis, Hardy M Hodges, George F Smoot,et al.Cosmic microwave background probes models of inflation[J].Phys Rev Lett,1992, 69, 1856.
[13]Scott D Friedman,George F Smoot,Giovanni De Amici,et al.Measurement of the cosmic background radiation temperature at 3.0 cm[J].Phys Rev,1984,D 29, 2677.
[14]Smoot G F,Gorenstein M V, Muller R A.Detection of Anisotropy in the Cosmic Blackbody Radiation[J].Phys Rev Lett,1977,39, 898.
[15]Panigrahi D,Chatterjee S .General Relativistic Plasma as window for Higher Dimensions[J].arXiv:gr-qc/0803.4449v1 31 Mar 2008.

