基于CFD的双幅桥梁气动干扰效应数值仿真

李 黎， 叶 醒， 李素杰， 彭元诚

(1 华中科技大学土木工程与力学学院， 湖北 武汉 430074；2 华中科技大学控制结构湖北省重点实验室， 湖北 武汉 430074；3 中交第二公路勘察设计研究院有限公司，湖北 武汉430056)

双幅桥面桥梁由于主梁距离较近，在气流作用下，上游桥面与下游桥面之间存在一定的相互影响，这种影响被称为双幅桥面的“气动干扰效应”[1]．国内外学者们对不同类型钝体绕流进行过大量的试验研究和数值模拟[2-5]，研究结果表明钝体之间存在气动干扰效应，并会对其绕流特性产生严重影响．Akihiro Honda[6]通过节段模型风洞试验研究了Kansai International Airport Access Bridge的气动稳定性，结果表明桥面之间的气动干扰对桥梁的气动稳定性有明显的影响．郭春平、白桦[7]等通过计算流体动力学(CFD)的方法，研究了三水河特大连续刚构桥三分力系数气动干扰效应，发现气动干扰效应不容忽视．对于三分力系数的计算，目前主要采用风洞试验和CFD数值模拟研究两种方法，风洞试验具有成本高、周期长的局限性，随着计算机技术的发展，计算机流体力学(CFD)为双幅桥面主梁三分力系数气动干扰效应研究提供了一条捷径．本文基于CFD方法，以北盘江特大桥工程为背景，研究不同风速条件下主梁间距和风攻角对双幅桥主梁三分力系数气动干扰效应的影响．

1 计算模型和计算方法

1.1 基本思路与控制方程

三分力系数数值模拟的基本思路是将微分方程表示的数学模型离散为代数方程的形式,对代数方程求解，得到计算区域内各节点的速度和压力以及断面的阻力、升力和升力矩,将三分力无量纲化得到三分力系数[8]．体轴坐标系下的三分力系数定义如下：

Cd=2Fd/ρU2H,

(1)

Cl=2Fl/ρU2B,

(2)

Cm=2MT/ρU2B2.

(3)

式中：H为桥梁断面的高度；B为断面宽度；U为来流风速；ρ为空气密度，取1.225 kg/m3．

主梁纵向尺度大，计算模型近似按二维处理，数学模型采用雷诺时均N-S方程．为考虑湍流效应，引入常用的S-A单方程湍流模型．二维定常不可压控制方程可表示为：

(4)

(5)

(6)

(7)

1.2 计算模型与边界条件

北盘江特大桥主桥为双幅预应力混凝土空腹(斜腿)式连续刚构，以距桥梁中心线124 m处截面为特征断面进行研究(图1)．梁高h=4.65 m，梁宽B=10.5 m，上下游两桥面的间距D=0.5 m．

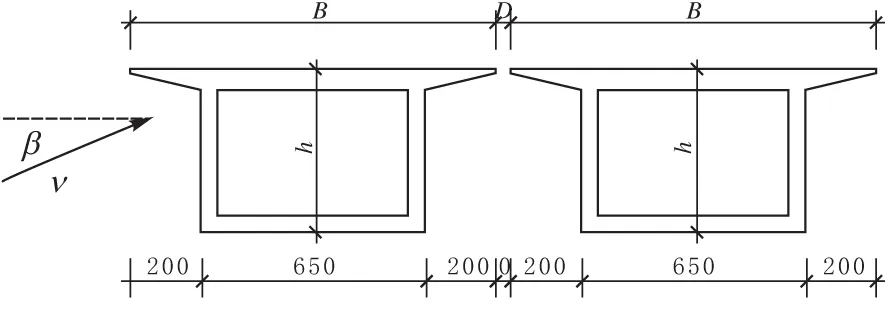
图 1 主梁特征截面 cm

本研究以主梁间距、风攻角和风速为研究参数，D值分别取D=0.108h和D=h、D=4h；风速3～21 m/s每隔3 m/s取值；风攻角取±10°、±5°、0°这5种工况．

CFD数值模拟时，建立双幅主梁和流域的计算模型(图2)．入口边界距上游主梁为15 B，出口边界距下游主梁为25 B，B为主梁宽．绕流时采用结构化网格，在主梁周围区域进行网格加密(图3～图4)，近壁面最小网格尺寸可用式(8)估算第一层网格的高度Δy满足y+≈1的要求．空气密度ρ=1.225 kg/m3，运动粘性系数ν=1.545×10-5m2/s．边界条件如下设置[9]：入口边界中设置速度入口，出口边界为出流边界条件，上下边界采用对称边界，主梁采用壁面边界．

(8)

图 2 双幅桥面主梁CFD计算域

图 3 流场网格划分(D=0.5 m，β=0°)

图 4 近壁区网格(D=0.5 m，β=0°)

2 可行性验证

为验证本文方法的正确性，计算双幅主梁间距D=0.5 m，风攻角为0°，风速为10 m/s工况下的阻力系数Cd、升力系数Cl和扭矩系数Cm，并与风洞试验结果进行对比．Flunt计算迭代500步左右能得到稳定的三分力系数时程曲线．根据三分力系数时程曲线可以得到上游主梁三分力系数Cd1、Cl1、Cm1、和下游主梁三分力系数Cd2、Cl2、Cm2的平均值，见表1．上述气动系数的计算结果与长安大学风洞试验的响应结果吻合较好，因此本文的计算模型及方法能较好地模拟双幅桥面主梁的三分力系数．

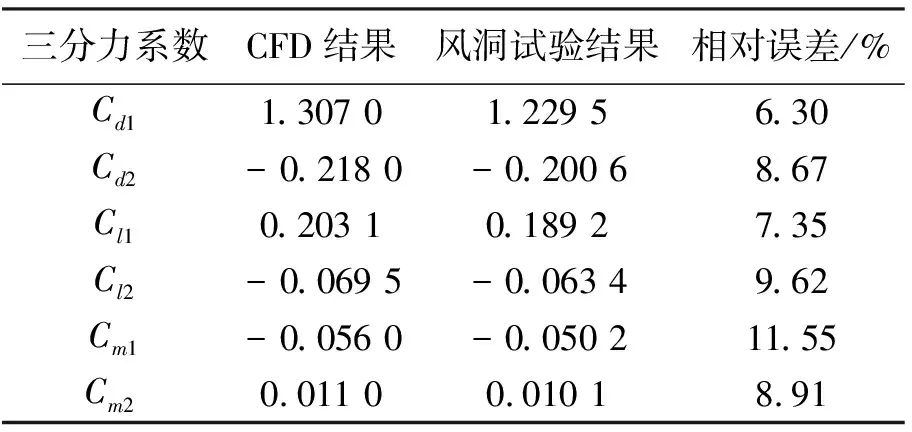
表1 CFD与风洞试验结果对比

3 双幅主梁三分力系数气动干扰效应数值模拟

本节基于CFD实现计算模型离散化研究双幅桥面主梁三分力系数气动干扰效应．双幅主梁影响因素主要有主梁间距、风攻角、来流风速等．计算仿真时，通过改变主梁水平间距D、风攻角β、来流风速V的取值，来研究它们对三分力系数气动干扰效应的影响．

另外，针对气动干扰效应影响，需引入适当的参数，以便进行量化分析．干扰效应的量化一般用干扰因子[10](Interference factor，IF)表示，定义如下：

(9)

式中，i取值为d、l、m，j取值为1、2．d为阻力系数，l为升力系数，m为扭矩系数；1为上游，2为下游．

3.1 主梁间距对气动干扰效应的影响

双幅桥面主梁在均匀来流作用下会发生气动干扰效应，首先就主梁间距对气动干扰效应的影响进行数值模拟．取风攻角保持0°不变，双幅桥面两主梁水平间距D分别取0.108h(0.5 m)、h、4h，计算得到不同主梁间距下三分力系数随来流风速V变化曲线如图5-7所示．

由图5-7可看出，与单幅桥相比，双幅桥上游主梁的存在对处在其尾流中的下游主梁影响很大，下游主梁的存在同时也对上游主梁有一定的影响.具体表现在以下几个方面：

1)与单幅桥相比，上游主梁阻力系数在D=0.108h和D=h时有一定增大，当D=4h时，其值又回到单幅桥阻力系数附近波动；然而，下游主梁阻力系数与单幅桥相比均有明显减小，且在D=0.108h和D=h时,阻力系数出现反号，即阻力方向发生逆转．

2)与单幅桥相比，上、下游主梁升力系数均明显减小，但减幅不同，下游主梁减幅更大；下游主梁在D=0.108h和D=h时，升力系数出现反号，也即升力方向发生逆转．

3)与单幅桥相比，上游主梁扭矩系数在D=0.108h和D=h时,显著减小，当D=4h时，又略微增大；下游主梁扭矩系数则减幅更大，在D=0.108h和D=h时，扭矩系数出现反号，扭矩方向也发生逆转．

4)风速对三分力系数均有影响，但影响很小．

为直观考察主梁间距对双幅桥气动干扰效应影响，按公式(9)处理，将计算结果绘制成不同主梁间距下气动干扰因子随来流风速V变化曲线．

图 5 阻力系数Cd随风速V变化曲线

图 6 升力系数Cl随风速V变化曲线

图 7 扭矩系数Cm随风速V变化曲线

由图8-10可看出：

1)双幅桥主梁间距D对上、下游主梁三分力系数气动干扰效应有一定影响，但与上游相比下游的干扰效应更为明显．

2)无论上游还是下游，随着主梁间距D的增大，主梁气动干扰因子越来越接近1，也即气动干扰效应越小．可以推想，当主梁间距足够大时，双幅桥相当于距离相隔很远的两孤立单幅桥，彼此对各自流场中压力与速度场的分布没有影响，其干扰因子为1．所以随着D的增大，干扰因子的极限值为1．

3)不同的分力系数，气动干扰效应也存在差别．对于阻力系数，上游主梁干扰因子在0.95～1.15之间，阻力系数变化幅度在14.3%以内；而下游主梁在D=4h时，干扰因子在0.4左右，阻力系数降低了近58.2%，D=0.108h和D=h时，阻力方向甚至发生逆转，因而干扰因子均小于0，呈现出负干扰．上游主梁升力系数干扰因子在0.4～0.5之间，升力系数降低了近55%；下游主梁升力干扰因子在D=4h时为0.22左右，降低了77.5%，D=0.108h和D=h时，升力方向也发生逆转，同样呈现负干扰．上游主梁扭矩系数干扰因子在0.3～1.1之间，而下游干扰因子在D=4h时为0.1左右，D=0.108h和D=h时，扭矩方向发生逆转，仍呈现出负干扰．

4)阻力系数干扰因子随风速增加而减小，然而变化不大；除D=4h外，升力系数干扰因子和扭矩系数干扰因子基本上不随风速变化，D=4h时，有一定波动，但幅度在19.3%以内．

图 8 阻力系数干扰因子随风速V变化曲线

图 9 升力系数干扰因子随风速V变化曲线

图10 扭矩系数干扰因子随风速V的变化曲线

3.2 风攻角对气动干扰效应的影响

风攻角对气动干扰效应也存在影响，因此，有必要对不同风攻角的双幅主梁气动干扰效应进行数值仿真研究．取D=0.5 m，风攻角取±10°、±5°、0°，计算得到不同风攻角下上、下游主梁三分力系数干扰因子随来流风速V变化曲线如图11-16所示．

由图11-13可看出：

1)上游主梁阻力系数气动干扰因子在0.9～1.2之间，与1相差不大，说明上游阻力系数与单幅桥相比变化不大，而此时风攻角的影响不能忽视，5°、10°时约为1，而0°、-5°、-10°时均基本大于1.05，风攻角为负值时对阻力系数的干扰效应比其值为正时大．

2)上游升力系数干扰因子取值在0.3左右，只是在10°突变为-0.15．

3)上游主梁扭矩系数干扰因子在风攻角为正时也在0.3左右取值，而负攻角时在-0.15左右．风攻角为负值时对阻力系数的干扰效应比其值为正时大．

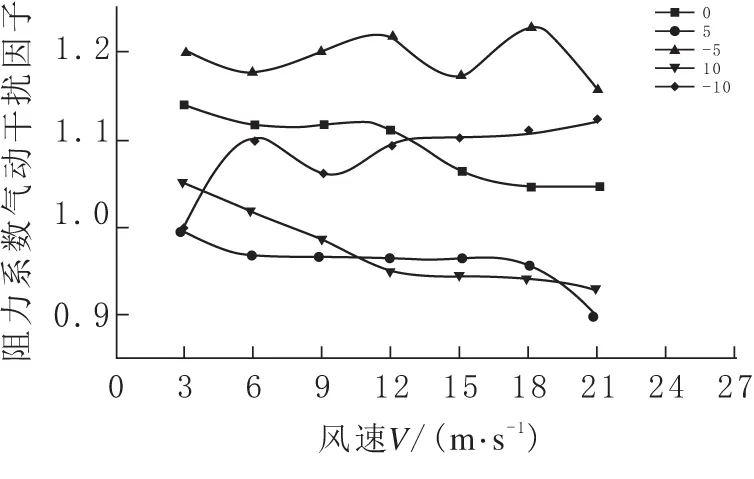
图11 上游阻力系数干扰因子随V的变化

图12 上游升力系数干扰因子随V的变化

图13 上游扭矩系数干扰因子随V的变化

由图14-16可看出，下游主梁阻力系数气动干扰效应随风攻角的增加而减弱．下游主梁升力系数表现为风攻角为正值时对升力系数的干扰效应比负值时大．下游主梁扭矩系数干扰效应随攻角的增加而增强．

图14 下游阻力系数干扰因子随风速V的变化

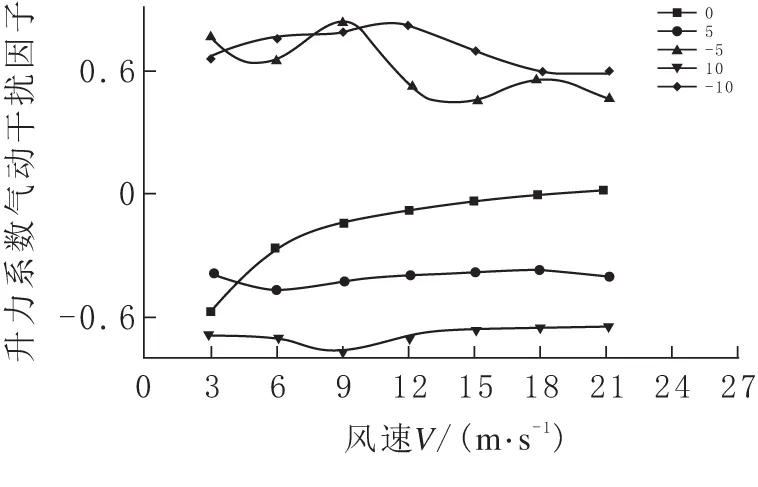
图15 下游升力系数干扰因子随风速V的变化

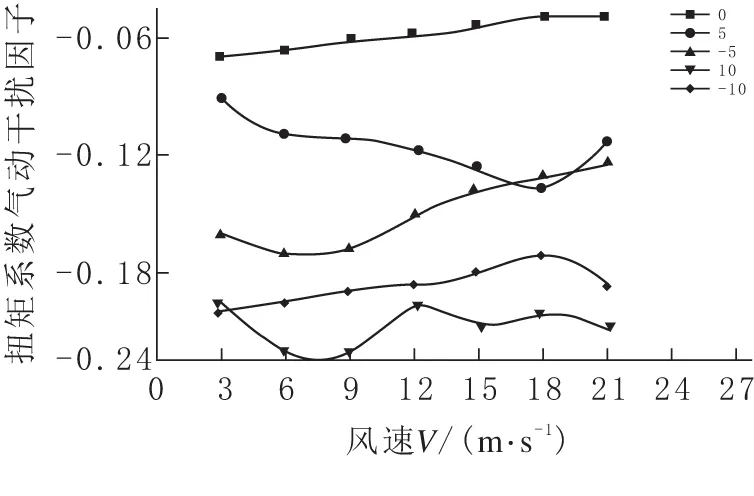
图16 下游扭矩系数干扰因子随风速V的变化

4 结束语

1)根据计算流体力学基本原理，将微分方程表示的数学模型离散为代数方程．借助Fluent软件计算双幅桥主梁三分力系数，其结果与风洞试验吻合较好，误差约为8.73%，最大不超过12%．数值模拟可以有效的分析双幅桥主梁三分力系数的气动干扰效应，得到其气动特性．

2)与单幅桥主梁的三分力系数相比，双幅桥主梁上、下游三分力系数均存在一定的干扰效应．但上游主梁的存在对处在其尾流中的下游主梁影响比下游主梁对上游主梁的影响要显著得多．另外，在主梁间距D较小时，下游主梁三分力的方向与单幅桥相比均发生了逆转，而随着D的增大，无论上、下游，气动干扰效应均减小，干扰因子极限值为1，因而其速度场和压力场的分布最终应趋近于单幅桥的情形．风攻角和风速对气动干扰效应的影响随主梁位置和分力系数类型不同而改变．与间距和风攻角相比，风速的变化对三分力系数气动干扰效应的影响在低雷诺数条件下是有限的．

3)仿真结果表明：双幅桥主梁气动干扰效应不容忽视，根据设计的不同，其影响的大小和性质也会不同．对于特定的断面形式和主梁间距，设计时应做好专门的气动特性研究．

[参考文献]

[1] 栗小祜.大跨度双幅桥面桥梁涡激振动响应气动干扰效应研究[D].长沙：湖南大学，2009.

[2] Zdravkovich M M. Review of flow interference between two circular cylinders in various arrangements [J]. ASME Journal of Fluids Engineering, 1977, 99(4): 618-633.

[3] Zdravkovich M M. Review of interference induced oscillations in flow past two circular cylinders in various arrangements [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 28: 183-200.

[4] 楼小峰, 曹丰产, 林志兴. 串列钝体绕流的数值计算[J]. 同济大学学报, 2002, 30(5): 604-608.

[5] 陈素琴, 黄自萍, 沈剑华,等. 两串列方柱扰流的干扰数值研究[J]. 同济大学学报, 2001, 29(3): 320-325.

[6] Akihiro Honda. Aerodynamic stability of kansai international airport access bridge [J].Journal of Wind Engineering and Industrial Aerodynamics, 1990,33:369-376.

[7] 郭春平，白 桦，洪 光.双幅桥静分力系数气动干扰效应研究[J].重庆交通大学学报(自然科学版),2011,30(5):899-902.

[8] 瞿伟廉, 刘琳娜.基于CFD的桥梁三分力系数识别的数值研究[J].武汉理工大学学报,2007,29(7):85-88.

[9] 李 黎, 曹化锦, 陈元坤. 架空输电线的找形及舞动研究[J]. 华中科技大学学报(自然科学版), 2011, 39(1): 102-105.

[10] 汪 洁.高墩大跨连续刚构双幅桥风致干扰效应研究[D]. 西安: 长安大学图书馆,2010.