拓扑绝缘体表面台阶势垒的输运性质

王爱坤，王 惠，穆惠英，安兴涛

(1.河北科技大学理学院，河北石家庄 050018；2.河北化工医药职业技术学院化工系，河北石家庄 050026)

拓扑绝缘体因为具有特殊的能带结构和电子性质[1]，近年来引起了人们广泛的关注和极大的兴趣。拓扑绝缘体是一种不同于金属和绝缘体的新的量子物质态，其时间反演不变性更是受到人们的关注。三维拓扑绝缘体的表面是个二维体系，有奇数个狄拉克点，在这些狄拉克点附近，电子的行为类似于无质量狄拉克费米子，遵守狄拉克方程[2-3]。这种无质量的狄拉克费米子具有线性色散关系，引起了非常奇特的量子输运现象，比如克莱因隧穿[4]——电子在垂直入射情况下穿过势垒可达到完全透射。正是由于这些迷人的重要特征，使拓扑绝缘体在未来的电子技术发展中有着巨大的应用潜力，所以研究拓扑绝缘体表面态的输运性质成为了人们目前关注的焦点。

近几年来，人们研究了拓扑绝缘体表面上单势垒、双势垒和多势垒的电子输运性质。GAO等研究了拓扑绝缘体表面上单垒和双垒的隧穿性质，他们发现可以调节克莱因隧穿，甚至可以阻止克莱因隧穿，这些特殊的性质使控制“拓扑金属”中的电子束变成了可能[4]。在他们研究的基础上，像电子准直器、波矢滤波器、电磁开关等新兴器件都可以制作出来。ZHANG等在周期变化的磁场下研究了三维拓扑绝缘体表面上狄拉克电子的输运性质，当势垒中磁场方向平行时，狄拉克点可以移动；而当势垒中磁场方向逆平行时，狄拉克点的位置不变[5]。另外，YOKOYAMA等研究了拓扑绝缘体表面铁磁体的输运性质，发现电导取决于2个铁磁体的磁场方向，磁场方向平行时的电导比磁场方向逆平行时的电导要小得多[6]。通过人们的不断研究，拓扑绝缘体表面态的性质一一被发现，但是拓扑绝缘体表面上的台阶势垒会对电子输运性质有什么影响还未见报道。

本文利用传递矩阵理论[7-10]研究了三维拓扑绝缘体表面上的台阶势垒的输运性质，通过调整台阶势垒的高度来研究拓扑绝缘体表面的隧穿性质，并计算台阶势垒的透射概率和电导[11-18]。研究中发现：当电子垂直入射势垒时，会出现全透射，这就是克莱因隧穿，但是无论势垒的高度如何，克莱因隧穿出现的位置是不变的。另外，随着费米能级的变化，电导有复杂的振荡行为并出现了共振隧穿现象；而随着台阶势垒高低势能差的变化，电导出现了开关效应，那么就可以通过调节费米能级和台阶势垒高低势能差来控制电导。这些研究不仅对理解材料的基本性质是至关重要的，而且对新器件的设计和发展有着重要的意义。

1 模型和方法

选取的模型是拓扑绝缘体表面上的台阶势垒，选取(x,y)平面代表拓扑绝缘体表面。为了简化，假设将台阶势垒分成2个高度不同的势垒，而2个势垒的宽度同为a，这样就将拓扑绝缘体表面分成4个区域，如图1所示，各个区域的势能可以表示为

图1 拓扑绝缘体表面台阶势垒的示意图Fig.1 Schematic diagram of the step barrier on the surface of a topological insulator

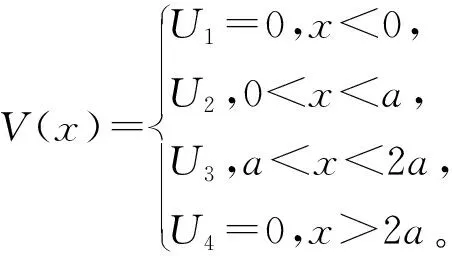
(1)

考虑拓扑绝缘体表面中的单电子近似法，可由静态无质量狄拉克方程表示为

(vFσP+Vxσ0)Ψ=EΨ。

(2)

式中：费米速度vF≈0.86×106ms-1；σ是泡利矩阵；P=(px,py)是电子动量；σ0是一个2×2的单位矩阵。

因为在本模型中，系统沿y方向是均匀的，所以横向波矢ky是守恒的。对于给定的入射能E，式(2)的解为

(3)

式中kx是纵向波矢，满足

(4)

根据波函数在边界的连续性，可知x=0时，Ψ1|x=0=Ψ2|x=0，即

(5)

利用传递矩阵方法可得

(6)

所以

(7)

x=a时，Ψ2|x=a=Ψ3|x=a,即

可得

(8)

所以

(9)

x=2a时，Ψ3|x=2a=Ψ4|x=2a，即

可得

(10)

所以

(11)

因此，总的传递矩阵为

Ts=T3T2T1。

(12)

势垒的反射系数和透射系数满足式(13)所示的方程：

(13)

最后可得透射概率为

T=|t|2。

(14)

根据Landauer-Bwttiker公式，系统的电导可以写成

(15)

图2 电子穿过台阶势垒的透射概率随入射角的变化关系Fig.2 Transmission probability of electrons through the step barrier as the function of the incident angle

式中：Ly≫2a是y方向的长度；φ=arccos(kx/EF)，是x方向的入射角；G0=2e2EFLy/(πh)，用它来作电导的单位。

2 结果和分析

在下面的数值计算中，取所有的参数为无量纲参数：以a=50 nm作为长度的单位，E0=hvF/a作为能量的单位(E0≈16．6 meV)，取图1中区域2和区域3的宽度为1，而且取台阶势垒低势能(U2=15E0)为固定值，而高势能U3是变化的，高低势能的电势差表示为dv=U3-U2。图2给出的是透射概率随入射角的变化关系，其中入射能E=10E0。

从图2可以看到，无论台阶势垒的高势能U3怎样变化，当电子垂直入射时，都会出现全透射，这就是克莱因隧穿，而且透射概率的曲线关于入射角是对称的。研究发现当台阶势垒的低势能U3=20E0时，曲线除了电子垂直入射时出现的克莱因隧穿点之外，又在-0.13π和0.13π处附近出现了2个克莱因隧穿点。此外，随着台阶势垒高势能U3的增大，这2个克莱因隧穿点不会再出现，而且它们的位置在逐渐地下降。这是因为当台阶势垒高势能U3变得极大时，台阶势垒低势能U2对电子隧穿的影响就会变得极小，几乎可以忽略不计，其结果相当于电子直接穿过单势垒。

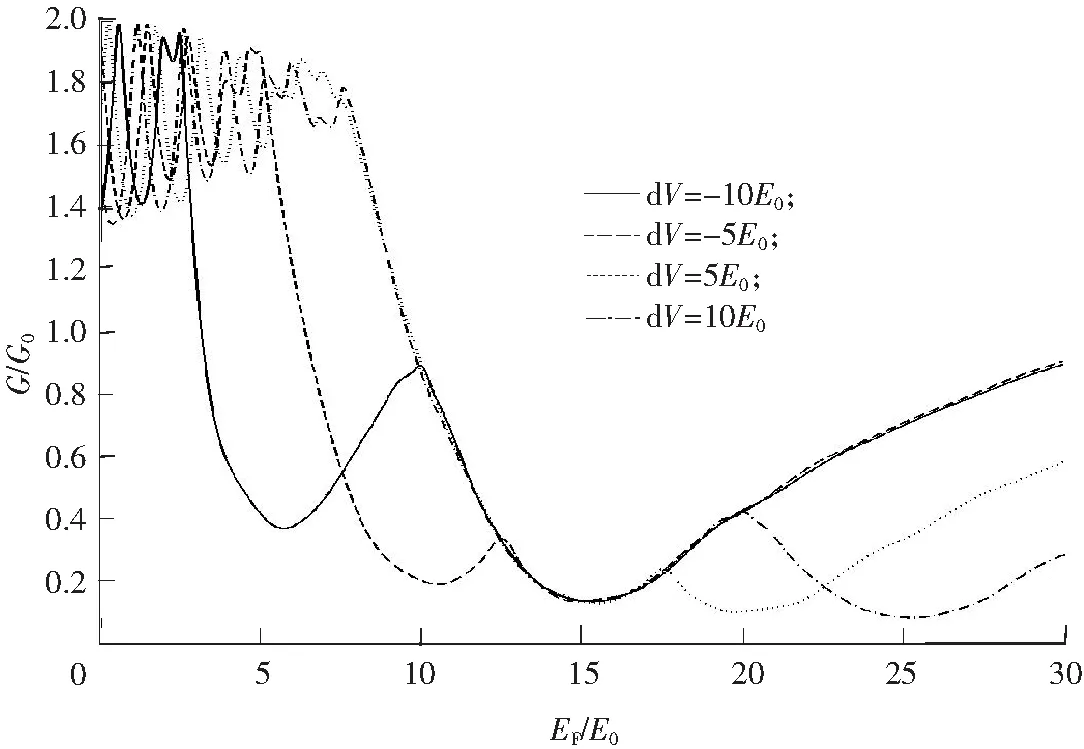
图3 拓扑绝缘体表面台阶势垒中电导随费米能级的变化关系 (U2=15E0)Fig.3 Conductivity as a function of the Fermi energy for the step barrier on the surface of a topological insulator (U2=15E0)

拓扑绝缘体表面台阶势垒中电导随费米能级的变化关系如图3所示。从图3可以看出，当费米能级小于台阶势垒低势能时，电导曲线随着费米能级的变化复杂地振荡，出现了共振隧穿效应，这时费米能级比较小，电子要穿过整个势垒，致使电导很大，甚至最大达到2G0；当费米能级与台阶中2个势垒的势能相等时，电导曲线形成低谷，均取得最小值，这样就可以通过调整费米能级的值来控制电导；当费米能级大于台阶势垒高势能时，电导曲线是随着费米能级的增加而增加的。在台阶势垒的高低势差值不断变化的情况下，势垒U2是固定的，费米能级等于台阶势垒的低势垒的势能时，电导G的值是相同的；而随着台阶势垒的高低势差值的增加，费米能级等于高势能处电导G的值是减小的。

图4 拓扑绝缘体表面台阶势垒中电导随高低势能差的变化关系(U2=15E0)Fig.4 Conductivity as a function of the difference of the step barrier on the surface of a topological insulator(U2=15E0)

图4给出了拓扑绝缘体表面台阶势垒中电导随高低势能差的变化关系。从图4可以看出，电导G是随着高低势的差值小幅度平缓地振荡，却在dv=(EF-U2)处形成低谷，并达到最小值，而这个最小值随着费米能级向右移动，这就形成了开关效应，所以可以通过调节台阶势垒的高低势能差来控制电导。

3 结 语

通过传递矩阵的方法研究了拓扑绝缘体表面上台阶势垒的透射概率和电导，发现了透射概率与台阶势垒的静电势有直接关系，而且在拓扑绝缘体表面存在克莱因隧穿，但是无论台阶势垒的静电势怎样变化，克莱因隧穿出现的位置是不变的。另外，随着费米能级的变化，电导有复杂的振荡行为并出现了共振隧穿现象；而随着台阶势垒高低势能差的变化，电导出现了开关效应，所以可以通过调节费米能级和台阶势垒高低势能差来控制电导。

参考文献/References：

[1] 叶 飞，苏 刚.拓扑绝缘体及其研究发展[J]. 物理，2010，39(8)：54-59.

YE Fei，SU Gang. Topological insulators[J]. Physics，2010，39(8) ：54-59.

[2] PHAM C，NGUYEN H，NGUYEN V L. Massless dirac fermions in a grapheme superlattice:At-matrix approach[J]. J Phys Condens Matter，2010，22：5 501-5 507.

[3] PRATIM R，TARUN K，KAUSHIK B. Localization of dirac-like excitations in grapheme in the presence of smooth inhomogeneous magnetic fields[J]. J Phys Condens Matter,2012，24(5)：5 301-5 312.

[4] GAO Jinhua，CHEN Weiqiang，FENG Xiaoyong，et al.Tunneling through ferromagnetic barriers on the surface of a topological insulator[J]. Mesoscale and Nanoscale Physics，2009，9：378-388.

[5] ZHANG Ya，ZHAI Feng. Tunneling magnetoresistance on the surface of a topological insulator with periodic magnetic modulations[J].Appl Phys Lett,2010，96(5)：36-38.

[6] YOKOYAMA T，TANAKA Y，NAGAOSA N.Anomalous magnetoresistance of a two-dimensional ferromagnet/ferromagnet junction on the surface of a topological insulator[J]. Phys Rev B，2010,81(12)：1 401-1 404.

[7] WANG Suxin，LI Zhiwen，LIU Jianjun，et al. Transport properties through double-magnetic-barrier structures in grapheme[J]. Chin Phys B，2011，20(7)：7 305-7 309.

[8] ZHAO Peiliang，CHEN Xi. Electronic band gap and transport in Fibonacci quasi-periodic grapheme superlattice[J]. Appl Phys Lett,2011，99：1-4.

[9] 张红梅，刘 德.传递矩阵方法与矩形势垒的量子隧穿[J] .河北科技大学学报，2006,27(3)：196-199.

ZHANG Hongmei，LIU De.Transfer matrix method in the study of quantum transmission for rectangular barrier[J].Journal of Hebei University of Science and Technology，2006,27(3)：196-199.

[10] 刘 德，张红梅，王博瑜.双势垒异质结构中自旋相关的散粒噪声[J].河北科技大学学报，2010,31(6)：512-516.

LIU De，ZHANG Hongmei，WANG Boyu.Spin-dependent shot noise in double barrier heterostructures[J].Journal of Hebei University of Science and Technology，2010, 31(6)：512-516.

[11] CONCHA A Z. Effect of velocity barrier on the ballistic transport of dirac fermions[J]. Phys Rev B，2010，82(3)：3 413-3 417.

[12] WANG Ligang，ZHU Shiyao. Electronic band gaps and transport properties in grapheme superlattices with one-dimensional periodic potentials of square barriers[J]. Phys Rev B，2010，81(20)：5 444-5 448.

[13] SUN Lifeng，FANG Chao，SONG Yu，et al. Transport properties through grapheme-based fractal and periodic magnetic barriers[J]. J Phys Condens Matter,2010，22：5 303-5 307.

[14] HOSEIN C，FATEMEH A. Spin polarization and magnetoresistance through a ferromagnetic barrier in bilayer grapheme[J]. J Phys Condens Matter,2012，24(4)：5 303-5 306.

[15] YOUNG H，YOONBAI K，CORNELIU S，et al. Landau level spectrum for bilayer grapheme in a tilted magnetic field[J]. J Phys Condens Matter,2012，24(4)：5 501-5 507.

[16] MICHAEL B，PEETERS F M，VASILOPOULOS P，et al. Dirac and Klein-Gordon particles in one-dimensional periodic potentials[J]. Phys Rev B，2008，77：5 446-5 450.

[17] LUCA D，ALESSANDRO D. Multiple magnetic barriers in grapheme[J]. Phys Rev B，2009，79(16)：5 420-5 428.

[18] ABEDPOUR N，AYOUB E，REZA A，et al. Conductance of a disordered grapheme superlattice[J]. Phys Rev B，2009，79(16)：5 412-5 419.