单位商品价值量与劳动生产力不可能成正比*
冯金华
(上海财经大学 马克思主义研究院,上海200433)
一、引 言
单位商品价值量与生产该种商品的整个部门的劳动生产力成反比,这是理解政治经济学“枢纽”的劳动二重性的直接推论,也是商品生产的一个基本规律。“成反比”是否正确,直接关系到如何理解劳动价值论、剩余价值论进而整个马克思主义经济学。
近年来有学者对“成反比”的规律提出异议。他们认为,20世纪以来,随着科学技术的突飞猛进,许多国家尽管在直接生产过程中的劳动总量不断下降,但国内生产总值却持续上升,因而出现了所谓的“世纪之谜”(李翀,1988)。世纪之谜是对马克思劳动价值论的“极大挑战”,因此有必要“重新理解”商品价值量和劳动生产力的规律(马艳和程恩富,2002)。
为了解释世纪之谜,一些学者提出,在一定的条件下,某种商品的单位价值量与生产它的部门劳动生产力有可能成正比。①其中有代表性的观点可表述为:引起劳动生产力变化的原因分为两类:一类是劳动的客观条件(如自然力、原材料和机器设备等)的变化,另一类是劳动的主观条件(如劳动强度、劳动熟练程度和劳动复杂程度等)的变化。劳动生产力的提高如果由单纯的客观条件变化引起,则它与单位商品价值量成反比;反之,如果由单纯的主观条件变化引起,则它与单位商品价值量就成正比。如果由客观和主观条件的共同变化引起,则劳动生产力与单位商品价值量就既可能成反比,也可能成正比(马艳和程恩富,2002)。
然而,所谓的世纪之谜其实是不存在的,因为国内生产总值并不是价值总量,而是价格总量,国内生产总值的增长只是价格总量而非价值总量的增长,而价格总量完全可以在劳动总量(从而价值总量)不变甚至下降的情况下上升。这一点与马克思的劳动价值论并无任何矛盾。
试图用区分劳动主客观条件的办法来解释“成正比”显然也缺乏说服力。与劳动客观条件的变化一样,如果某种劳动主观条件的变化提高了劳动生产力,即提高了单位劳动所生产的产量,则它一定会降低单位产量中所包含的劳动量,即降低单位商品的价值量;反之,如果某种劳动主观条件的变化提高了单位商品的价值量,即提高了单位产品中包含的劳动量,则它一定会降低单位劳动所生产的产量,即降低劳动生产力。②特别是,如果由物质资本和人力资本的变化导致的物化劳动和复杂劳动的变化使劳动生产力提高了,则它一定会降低单位商品价值量;反之,如果它使单位商品价值量提高,则一定会降低劳动生产力。③这是根据劳动生产力和单位商品价值量的定义即可明白的事理。
一些学者之所以会得出单位商品价值量与劳动生产力有可能成正比的结论,是因为他们没有看到,任何一种生产要素的增加,无论它是属于劳动客观条件的变化,还是属于劳动主观条件的变化,通常都会导致产量的增加,也可能会导致劳动的增加。例如,物质资本的增加意味着蕴含在物质资本中的物化劳动的增加,人力资本的增加意味着蕴含在人力资本中的复杂劳动的增加。④劳动生产力和单位商品价值量究竟如何变化要看这两方面作用的相对大小。如果某种生产要素的增加,导致产量增加的程度大于劳动增加的程度,则显然就有劳动生产力上升和单位商品价值量下降;反之,如果导致产量增加的程度小于劳动增加的程度,则显然就有劳动生产力下降和单位商品价值量上升。如果导致产量增加的程度恰好等于劳动增加的程度,则劳动生产力和单位商品价值量都将保持不变。在前两种(也是非常一般的)情况下,单位商品价值量与劳动生产力总成反比,在最后这种(也是非常个别和偶然的)情况下,单位商品价值量与劳动生产力既不成反比,也不成正比。换句话说,无论在什么样的条件下,单位商品价值量与劳动生产力都不可能成正比。这个结论既适用于自然资源和物质资本的变化,也适用于简单活劳动和人力资本的变化,既适用于劳动客观条件的变化,也适用于劳动主观条件的变化。
“成正比”学派的问题在于,他们在定义劳动生产力和单位商品价值量时,分别使用了内容并不相同的劳动概念。例如,他们在计算单位商品价值量时,通常会把物化劳动和复杂劳动考虑在内,但在计算劳动生产力时,往往又会“忘掉”物化劳动和复杂劳动。实际上,无论是计算劳动生产力,还是计算单位商品价值量,如果都始终如一地使用相同的劳动概念,即在计算单位商品价值量时不仅包括简单活劳动,而且包括物化劳动和复杂劳动;在计算劳动生产力时也同样不仅包括简单活劳动,而且包括物化劳动和复杂劳动,就一定会得到与马克思完全相同的结论,即一般而言,单位商品价值量与劳动生产力总是成反比,而不可能成正比。
进一步分析,“成正比”学派产生这些问题的根源在于没有正确理解劳动二重性这个“枢纽”。实际上,无论是简单活劳动,还是物化劳动或者复杂劳动,都具有劳动的二重性,即都具有具体劳动和抽象劳动两重属性,从而既可以用于计算劳动生产力——劳动生产力总是具体劳动的生产力,也可以用于计算商品的价值量——商品价值量是人类抽象劳动的凝结。正如马克思所说:“一切劳动,一方面是人类劳动力在生理学意义上的耗费;就相同的或抽象的人类劳动这个属性来说,它形成商品价值。一切劳动,另一方面是人类劳动力在特殊的有一定目的的形式上的耗费;就具体的有用的劳动这个属性来说,它生产使用价值。”⑤换句话说,所谓具体劳动和抽象劳动,不过是同一劳动过程的两个方面。二者不可能独立存在。因此,把某种劳动(例如复杂劳动)看成只具有抽象劳动的属性,从而只能用于计算商品的价值量而不能用于计算劳动生产力的观点是不能成立的。
为明确起见,本文假定所讨论的都是所谓的“劳动产品”,即都是简单或复杂的活劳动的产品。⑥因此,当简单活劳动和复杂活劳动的数量都为零时,产出自然为零。换句话说,活劳动是生产过程中必不可少的生产要素。此外,还假定自然资源的边际产出不等于零,即随着自然资源的变化,产出总会变化。⑦
根据上述假定,本文分别讨论自然资源、简单活劳动、物质资本和人力资本的变化对劳动生产力和单位商品价值量的影响,并说明在所有这些场合,单位商品价值量与劳动生产力都不会成正比,特别是它们在绝大多数的情况下都成反比,而在极个别的例外情况下既不成反比也不成正比。
二、自然资源和简单活劳动
如果在某种产品的生产过程中只消耗直接的简单活劳动(其数量用L表示),以及一些不需要经过劳动即可以得到的自然资源(其数量用R表示),并不使用蕴含着物化劳动的物质资本和表现为复杂劳动的人力资本,则该产品的生产函数就可写为Q=Q(R,L),且根据假定有Q(R,0)=0以及∂Q/∂R≠0。
由于在上述两要素模型中只有直接的简单活劳动,而不存在任何其他形式的物化劳动或复杂劳动,故劳动生产力(用a表示)的概念显得非常简单和清楚,很少会有歧义。它可以表示为:

容易看到,式(1)定义的其实可以称为“简单活劳动生产力”,因为这里并不存在任何其他形式的劳动。
同样,在这种情况下,单位商品价值量(用z表示)的概念也非常清楚。它可由式(2)决定:

这是因为,根据马克思的劳动价值论,一个部门的劳动总量就是它的社会必要劳动总量或价值总量,从而这个部门的单位商品价值量就是其劳动总量与产出总量的比率。由于在两要素模型中只有简单活劳动,故单位商品价值量就等于简单活劳动总量除以产出总量。
下面要利用式(1)和式(2)更具体地说明单位商品价值量与劳动生产力在哪些情况下成反比,在其余情况下既不成反比,也不成正比,从而总的来说,在所有的情况下都不可能成正比,并借助这些公式,在考虑物化劳动和复杂劳动更加一般的情况下推导单位商品价值量与劳动生产力关系的变形和发展。

由式(1)和式(2)显而易见有:换句话说,单位商品价值量与劳动生产力成反比。
但这里需要注意的是,上述定义劳动生产力和单位商品价值量的式(1)和式(2),从而关于单位商品价值量与劳动生产力成反比的式(3),在简单活劳动等于零时不再成立。这是因为,当简单活劳动为零时,产出亦为零,式(1)和式(2)的右边都是0/0的“不定式”。这意味着劳动生产力和单位商品价值量都是不确定的,从而二者之间的关系亦无从谈起。
除了简单活劳动为零这种没有什么现实意义的极端情况之外,在所有其他场合(包括自然资源等于零或不等于零),式(1)、式(2)和式(3)都是成立的。例如,当自然资源等于零但简单活劳动大于零时,如果产出此时大于零,则根据式(1)和式(2),劳动生产力a和单位商品价值量z都大于零,且互为倒数;另一方面,如果产出此时等于零,则同样根据式(1)和式(2),劳动生产力a为零,单位商品价值量z趋于+∞,二者仍然成反比。
由此可见,在只使用自然资源和简单活劳动的两要素模型中,只要简单活劳动的数量不等于零,单位商品价值量与劳动生产力就成反比。
上述结论意味着在简单活劳动大于零的情况下,随着某种生产要素的增加,如果劳动生产力是提高的,则单位商品价值量就下降;反之,如果劳动生产力是下降的,则单位商品价值量就提高。但是,如果随着某种生产要素的增加,劳动生产力并不变化,则单位商品价值量也不会变化。在这种情况下,单位商品价值量与劳动生产力就不存在所谓的反方向变化。
因此,需要进一步讨论的是单位商品价值量和劳动生产力在什么样的条件下会随某种生产要素的变化而变化,从而存在成反比的关系,又在什么样的条件下不随某种要素的变化而变化,从而不存在成反比的关系。
首先,自然资源对劳动生产力和单位商品价值量的影响可由式(1)和式(2)中的a和z对R的一阶偏导数来表示:

容易看到,这两个偏导数∂a/∂R和∂z/∂R的符号总是相反的。这意味着随着自然资源的增加,如果自然资源的边际产出大于零,即∂Q/∂R>0,劳动生产力就会上升,而单位商品价值量就会下降,即有∂a/∂R>0和∂z/∂R<0;反之,如果自然资源的边际产出小于零(尽管这种情况不太符合实际),劳动生产力就会下降,而单位商品价值量就会上升。无论如何,二者总是反方向变化。只有在自然资源的边际产出等于零时,上述反方向变化关系才不再成立。这是因为,当∂Q/∂R=0时,式(4)中的两个偏导数都等于零,从而它们的符号不再相反。从这里可以看到,自然资源的变化之所以能够造成单位商品价值量和劳动生产力反方向变化,是因为自然资源的边际产出不等于零,或者说自然资源的变化总能导致产出的变化。如果自然资源的变化不能导致产出的变化,则它就不能够改变劳动生产力,也不能改变单位商品价值量,自然也就谈不上使二者反方向变化。
由此可见,在自然资源和简单活劳动的两要素模型中,只要自然资源的边际产出不等于零,则随着自然资源的变化,单位商品价值量与劳动生产力就会反方向变化。
其次,单位商品价值量和劳动生产力随简单活劳动的变化而变化的具体情况可由式(1)和式(2)中的a与z对L的一阶偏导数来表示:
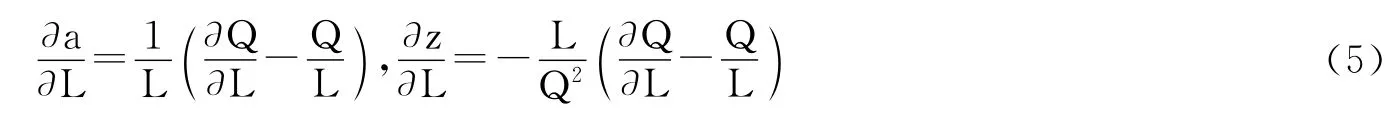
这两个偏导数∂a/∂L和∂z/∂L的符号也总是相反的。具体来说,随着简单活劳动的增加,如果劳动的边际产出大于劳动平均产出,即∂Q/∂L>Q/L,则劳动生产力就会上升,而单位商品价值量就会下降,即∂a/∂L>0,而∂z/∂L<0;反之,如果劳动的边际产出小于平均产出,则劳动生产力就会下降,而单位商品价值量就会上升。无论如何,二者同样总是反方向变化。只有在劳动的边际产出恰好等于劳动的平均产出时,上述反方向变化关系才不再成立。这是因为,当∂Q/∂L=Q/L时,式(5)中的两个偏导数都等于零,从而它们的符号不再相反。从这里也可以看到,简单活劳动的变化之所以能够造成单位商品价值量和劳动生产力反方向变化,是因为简单活劳动的边际产出不等于平均产出,或者说简单活劳动变化能够导致劳动平均产出的变化。如果简单活劳动的变化不能导致劳动平均产出的变化,则它就不能改变劳动生产力,也不能够改变单位商品价值量,从而也就谈不上使二者反方向变化。
三、物质资本和物化劳动
假定在某种产品的生产过程中,既消耗自然资源和简单活劳动,也消耗包括物化劳动在内的物质资本(其数量用K表示),但不使用包括任何复杂劳动的人力资本,则该产品的生产函数就可写为Q=Q(R,K,L),且有Q(R,K,0)=0,以及∂Q/∂R≠0。
由于在三要素模型中不仅消耗了简单活劳动,而且消耗了物质资本,从而也消耗了蕴含在物质资本中的物化劳动,故劳动生产力和单位商品价值量的概念变得复杂起来。在这种情况下,若要正确计算劳动生产力和单位商品价值量,就不仅应当考虑生产过程中直接消耗掉的简单活劳动,而且应当考虑间接消耗掉的蕴含在物质资本中的物化劳动。关于这一点,马克思曾有过多次明确论述:“劳动生产率的提高正是在于:活劳动的份额减少,过去劳动的份额增加,但结果是商品中包含的劳动总量减少;因而,所减少的活劳动大于所增加的过去劳动。……因此,加入商品的劳动总量的这种减少,好像是劳动生产力提高的主要标志,无论在什么社会条件下进行生产都一样。”⑧“很明显,如果生产一台机器所费的劳动,与使用该机器所节省的劳动相等,那么这只不过是劳动的变换,就是说,生产一个商品所需要的劳动总量没有减少,或者说,劳动生产力没有提高。”⑨
按照上述扩展的劳动消耗的概念,在同时使用自然资源、简单活劳动和物质资本的三要素模型中,劳动生产力的表达式也应当相应地发展为:⑪

与两要素模型中的简单活劳动生产力不同,式(6)定义为“简单劳动生产力”,因为这里的劳动包括所有的简单活劳动和简单物化劳动。简单劳动生产力常常也被称为“全劳动生产力”。但仔细分析,这里的“全”并不完全名副其实,因为它还没有包括复杂劳动。下文会看到,一旦考虑到生产过程中除了投入简单活劳动和物质资本之外,还要投入人力资本,则全部的劳动就不仅只包括简单活劳动和物化劳动,还必须包括复杂劳动。
在这种情况下,单位商品价值量的表达式也应当发展为:

由式(6)和式(7)显而易见亦有z=1/a。换句话说,在同时使用自然资源、简单活劳动和物质资本的三要素模型中,单位商品价值量与劳动生产力也总是成反比。
需要指出的是,与前述一样,在式(6)中,劳动生产力仍被定义为单位劳动生产的产品数量,在式(7)中,单位商品价值量仍被定义为单位商品中包含的劳动量,只是在这里,“单位劳动”和“单位商品中包含的劳动量”不再仅仅只有简单活劳动,也有(简单)物化劳动。
再看劳动生产力和单位商品价值量随自然资源、简单活劳动和物质资本变化而变化的规律,以及二者之间的相互关系。
首先,自然资源变化对劳动生产力和单位商品价值量的影响与两要素模型中的情况几乎完全相同,唯一的区别是,这里的劳动是“扩展”的,即同时包括简单活劳动和物化劳动,而不再是只包括简单活劳动。例如,由式(6)和式(7)分别对R求一阶偏导数得到:

只要自然资源的边际产出不等于零,单位商品价值量和劳动生产力就会随自然资源的变化而反方向变化。
其次,简单活劳动变化对劳动生产力和单位商品价值量的影响在形式上与两要素模型也没有多少差异。例如,由式(6)和式(7)分别对L求一阶偏导数得到:

这里需要注意的是,尽管这两个式子在形式上与两要素模型中的相应公式非常相像,但仍有细微的区别:在它们右边的括号中,第一项∂Q/∂L与前文一样是简单活劳动的边际产出,但第二项Q/()+L 却是简单活劳动和物化劳动(而非只是简单活劳动)的平均产出。于是,现在的结论为:只要简单活劳动的边际产出不等于全部劳动的平均产出,单位商品价值量和劳动生产力就会随简单活劳动的变化而反方向变化。
最后,物质资本变化对劳动生产力和单位商品价值量的影响可由式(6)和式(7)的两边分别对K求一阶偏导数得到:


两个偏导数∂a/∂K和∂z/∂K的符号也相反。这里,两式右边括号中的第一项(∂Q/∂K)/Q是因物质资本变化而导致的产出变化率,第二项 (/dK)/+L) 是因物质资本变化而导致的劳动变化率。因此,劳动生产力和单位商品价值量随物质资本变化而变化的规律完全取决于物质资本变化所导致的产出变化率和劳动变化率的相对大小。
从式(8)和式(9)可以看到,随着物质资本的增加,如果产出的增长率大于劳动的增长率,即(∂Q/∂K)/Q>(d/dK)/+L),则有∂a/∂K>0和∂z/∂K<0,即劳动生产力提高而单位商品价值量下降;反之,如果物质资本引起的产出增长率小于劳动的增长率,则劳动生产力就会下降,而单位商品价值量就会上升。如果物质资本引起的产出增长率恰好等于劳动的增长率,则劳动生产力和单位商品价值量就保持不变。换句话说,物质资本的变化之所以能够造成单位商品价值量和劳动生产力反方向变化,是因为物质资本变化所引起的产出的变化率不等于劳动的变化率。如果由物质资本变化引起的产出的变化率等于劳动的变化率,则它就不能够改变劳动生产力,也不能够改变单位商品价值量,自然也就谈不上使二者反方向变化。
在讨论同时存在简单活劳动和物化劳动的生产过程时,某些“成正比”学派存在的一个问题是,它一方面正确地根据全部的简单活劳动和物化劳动来计算单位商品价值量,另一方面又仅仅根据简单活劳动(而非同时包括简单活劳动和物化劳动的全部劳动)来计算劳动生产力。正是因为在计算单位商品价值量和劳动生产力时使用的是完全不同的劳动概念,才导致他们认为,随着物质资本的增加,单位商品价值量与劳动生产力有可能成正比:一方面,物质资本的增加只会增加产出而不会增加简单活劳动,故根据式(1),它总会提高简单活劳动生产力;另一方面,根据式(9),如果由物质资本增加引起的产出增长率小于劳动的增长率,则单位商品价值量就会上升。因此,在最后这种情况下,随着物质资本的增加,单位商品价值量与简单活劳动生产力就会成正比。由此可见,一些学者之所以在讨论物化劳动时会出现“成正比”的困惑,是因为他们仍然只是根据简单活劳动而非同时包括简单活劳动和物化劳动的全部劳动来计算劳动生产力。
四、人力资本和复杂劳动
我们可以将上述讨论劳动生产力与单位商品价值量及其相互关系时考虑物质资本和物化劳动的方法进一步推广到纳入人力资本和复杂劳动的一般模型中。
如果在某种产品的生产过程中既使用和消耗了自然资源、简单活劳动和物质资本,也使用和消耗了含有复杂劳动的人力资本(其数量用A表示),即同时使用和消耗了四种生产要素,则该产品的生产函数就应当表示为:Q=Q(R,K,A,L),且有 Q=Q(R,K,0,0)=0以及∂Q/∂R≠0。
在同时包括自然资源、简单活劳动、物质资本和人力资本的四要素模型中,劳动概念得到了进一步的拓展——它除了包括简单活劳动和物化劳动之外,还包括体现在人力资本中的复杂劳动。相应地,在计算劳动生产力和单位商品价值量时,就不仅需要考虑简单活劳动和物化劳动,而且需要考虑复杂劳动。
需要注意的是,由于复杂劳动是体现在人力资本上的活劳动,相当于多倍的简单劳动,故它不能与简单活劳动和简单物化劳动直接相加,而必须先进行“换算”。例如,假定1个单位的复杂劳动等于h(h>1)个单位的简单劳动,则个单位的复杂劳动就等于h个单位的简单劳动。可称为“简单化后的”复杂劳动。这样,通过转换系数h,便可以把复杂劳动转化为简单劳动,从而可以把简单化后的复杂劳动和简单活劳动与物化劳动相加,求得四要素模型中的全部劳动
根据上述对四要素模型中生产函数和劳动总量的说明,劳动生产力和单位商品价值量的表达式显然可以分别写为:
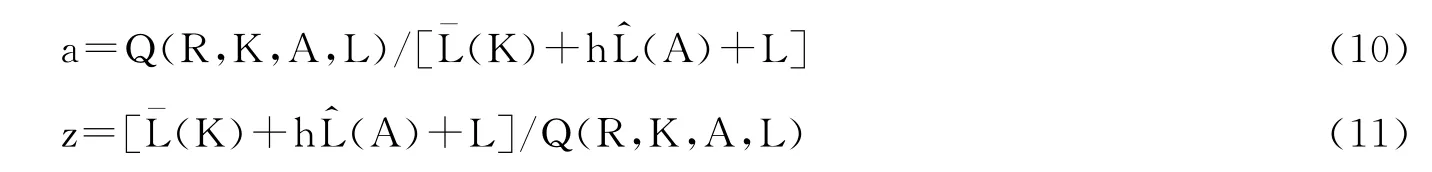
显然有z=1/a,即在四要素模型中单位商品价值量与劳动生产力也成反比。
相对于两要素模型中的简单活劳动生产力和三要素模型中的简单劳动生产力,由式(10)所定义的可称为“全劳动生产力”或“总劳动生产力”,因为这里的劳动包括了所有的劳动,即既包括简单活劳动和简单物化劳动,也包括复杂劳动。
再看劳动生产力和单位商品价值量随不同生产要素变化而变化的情况。与三要素模型相比,在四要素模型中除了劳动已经被进一步扩展到同时包括简单活劳动、物化劳动和(简单化后的)复杂劳动之外,自然资源、简单活劳动、物质资本和人力资本对劳动生产力和单位商品价值量的影响方式与结果并无太大不同。
首先,劳动生产力和单位商品价值量对自然资源的一阶偏导数分别为:

只要自然资源的边际产出不等于零,单位商品价值量和劳动生产力就会随自然资源的变化而反方向变化。
其次,劳动生产力和单位商品价值量对简单活劳动的一阶偏导数分别为:

只要简单活劳动的边际产出不等于全部劳动的平均产出,单位商品价值量和劳动生产力就会随简单活劳动的变化而反方向变化。
再次,劳动生产力和单位商品价值量对物质资本的一阶偏导数分别为:
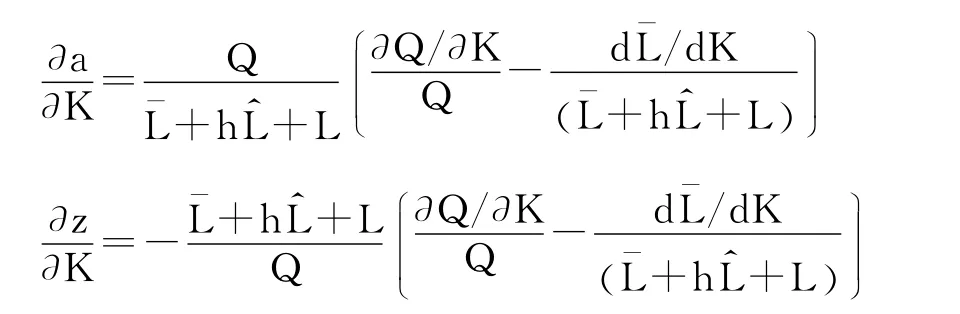
只要物质资本变化引起的产出变化率不等于全部劳动的变化率,单位商品价值量和劳动生产力就会随物质资本的变化而反方向变化。
最后,劳动生产力和单位商品价值量对人力资本的一阶偏导数分别为:

在讨论同时存在简单活劳动、物化劳动和复杂劳动的生产过程时,某些“成正比”学派存在的另一个问题是,它一方面正确地根据全部的简单活劳动、物化劳动和复杂劳动来计算单位商品价值量,另一方面又仅仅根据简单活劳动或简单活劳动和物化劳动(而非同时包括简单活劳动、物化劳动和复杂劳动的全部劳动)来计算劳动生产力。正是因为在计算单位商品价值量和劳动生产力时使用的是完全不同的劳动概念,才导致他们认为,随着人力资本亦即复杂劳动的增加,单位商品价值量与劳动生产力有可能成正比:一方面,人力资本的增加只会增加产出而不会增加简单活劳动或物化劳动,故根据式(1)或式(6),它总会提高简单活劳动生产力或简单劳动生产力;另一方面,根据式(12),如果由人力资本增加引起的产出增长率小于劳动的增长率,则单位商品价值量就会上升。因此,在最后这种情况下,随着人力资本的增加,单位商品价值量与简单活劳动生产力或简单劳动生产力就会成正比。由此可见,一些学者之所以在讨论复杂劳动时会出现“成正比”的困惑,是因为他们仍只根据简单活劳动和物化劳动而非同时包括简单活劳动、物化劳动和复杂劳动的全部劳动来计算劳动生产力。一旦我们使用正确的劳动概念,即按照全部劳动来计算劳动生产力和单位商品价值量,则在存在复杂劳动的条件下,“成正比”的困惑将不复存在。因为在这种情况下,如果复杂劳动增加(或劳动复杂程度提高)导致产量增加的程度小于劳动增加的程度,则按全部劳动计算的劳动生产力实际上就不是提高而是下降,从而,由劳动复杂程度提高导致的单位商品价值量的增加,也不是与劳动生产力成正比,而是成反比。
五、结 论
本文关于两要素、三要素和四要素模型的讨论可以推广到包括任意多种要素的一般模型,因此,任何一种生产要素,如果其增加导致的产出增长率大于全部劳动的增长率,则劳动生产力和单位商品价值量就分别随该要素的增加而上升和下降;反之,如果其增加导致的产出增长率小于全部劳动的增长率,则劳动生产力和单位商品价值量就分别随该要素的增加而下降和上升;最后,如果其增加导致的产出增长率恰好等于全部劳动的增长率,则劳动生产力和单位商品价值量就不随该要素的变化而变化。换句话说,在所有这些情况下,单位商品价值量与劳动生产力都不会成正比,而除了最后这种非常特殊和偶然的情况之外,单位商品价值量与劳动生产力都成反比。
注释:
①参见孟捷(2005、2011)对“成正比”理论的概括和分类。
②本文所说的劳动生产力都是就一个部门而言的,即部门的平均劳动生产力。
③即使是反对“成正比”的人,对这个问题也不是看得很清楚。例如,张衔(2011)认为,如果某种生产技术使劳动复杂程度的提高速度大于劳动生产力的提高速度,则单位商品价值量就会与劳动生产力“正相关”,但这样的生产技术是不会被采用的,“否则生产者将面临亏损而在竞争中处于不利地位”。实际上,这里的问题与生产者是否采用这样的生产技术并无关系,因为即使生产者采用这样的生产技术,单位商品价值量也不会与劳动生产力“正相关”,只要该生产技术提高了单位商品价值量,就一定会降低劳动生产力,反之亦然。
④有些生产要素如自然资源等不需要劳动来生产,故其增加只会导致产出的增加,而不意味着有相应的劳动增加。
⑤⑨马克思:《资本论(第1卷)》,人民出版社2004年版,第60页、第448-449页。
⑥按照马克思的劳动价值论,非劳动产品没有价值,故讨论它的价值量与劳动生产力的关系没有意义。
⑦自然资源的边际产出通常大于零。不过,即使它小于零也不会影响本文的结论。至于其他生产要素(如简单活劳动、物质资本和人力资本等),则不论它们的边际产出是否等于零,都不会影响本文的结论。
⑧马克思:《资本论(第3卷)》,人民出版社2004年版,第290页。
⑩计算同时包括简单活劳动和简单物化劳动的方法可参见Okishio(1963)。
⑪为简单起见,这里仍然用a和z分别代表三要素(以及其他)模型中的劳动生产力和单位商品价值量。
⑫尽管本文讨论的主要是复杂劳动的增加,但所使用的方法同样也适用于劳动复杂程度的提高。
⑬计算转换系数h和四要素模型中全部劳动的方法可参见Okishio(1963)。
[1] 李翀.论价值下降与价格上升的“世纪之谜”[J].价格理论与实践,1988,(6):27-33.
[2] 马艳,程恩富.马克思“商品价值量与劳动生产率变动规律”新探——对劳动价值论的一种发展[J].财经研究,2002,(10):43-48.
[3] 孟捷.技术创新与超额利润的来源:基于劳动价值论的各种解释[J].中国社会科学,2005,(5):4-15.
[4] 孟捷.劳动生产率与单位时间创造的价值量成正比的理论:一个简史[J].经济学动态,2011,(6):41-47.
[5] 张衔.劳动生产率与商品价值量关系的思考[J].教学与研究,2011,(7):54-59.
[6] Okishio N.A mathematical note on Marxian theorems[J].Weltwirtschaftliches Archiv,1963,91(2):287-299.

