限制对比度的多层POSHE自适应图像增强算法

杨 光，吴钟建，罗镇宝，王浩宇，张 龙

(1．西南技术物理研究所，四川成都610041;2．西南自动化研究所，四川 绵阳621000)

1 引言

图像增强的首要目标是处理图像，使其比原始图像更适合于特定应用，比如目标识别、跟踪等［1］。基于直方图均衡(HE)的图像增强方法以其简单快速的特点倍受青睐，全局直方图均衡(GHE)根据图像直方图计算灰度变换函数，对整幅图像像素作单一映射，没有考虑图像局部信息，造成部分高频信息丢失［2］。

基于局部直方图均衡(LHE)算法根据图像局部特性计算灰度变换函数，克服GHE难以适应局部灰度分布的缺陷，对比度增强效果较好，它的最初原型是Tom等人于1982年提出的自适应直方图均衡算法［3］(AHE)，过高的时间复杂度限制AHE算法的应用范围;Kim等人于2001年提出的子块部分重叠直方图均衡［4］(POSHE)算法，具有良好对比度增强效果，较AHE算法计算量明显减少，但是该算法存在明显块效应和局部过增强问题;翟艺书等人于2007年提出了一种改进的雾天图像清晰化方法［5］，利用移动模板对各局部区域作POSHE处理，一定程度增强图像对比度，但没有解决POSHE算法存在的块效应和过增强问题。通过分析POSHE算法的不足，提出限制对比度多层POSHE自适应图像增强算法 (contrast limited multilayered POSHE，CLMPOSHE)，在增强图像对比度和细节信息的同时，消除块效应和过增强现象。

2 POSHE算法

POSHE算法是一种典型的局部直方图均衡算法，步骤如下:将图像分为四个子块，以步长为子块一半为例，如图1所示，由九个非重叠的小区域(a～i)构成四个重叠的子块①(a，b，d和e构成)、子块②(b，c，e和f构成)、子块③(d，e，g和h 构成)和子块④(e，f，h和i构成)，四个子块重叠区域为e。首先对第①子块均衡，然后再对第②子块均衡，本行处理完毕转到下一行，以此类推，最后对子块重叠的区域进行加权处理［4］。公式如下所示:

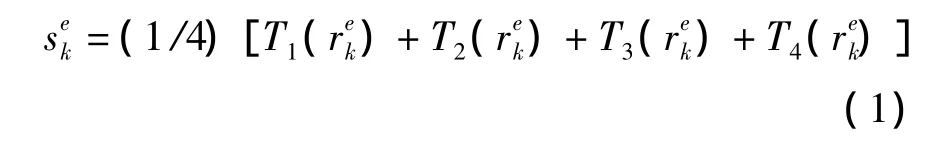
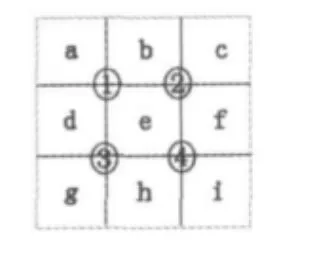
图1 子图

POSHE算法处理后的图像会出现块效应和过增强现象，块效应程度、增强效果与块大小和步长大小有关。

2．1 块效应程度与子块大小和步长的关系

图2是POSHE算法对同一幅图像在不同子块大小步长情况下的处理结果(M表示子块大小、λ表示步长)。

图2中，子图2(b)～图2(d)是块大小相同(均为M=64)，不同步长下的POSHE算法增强后的块效应程度。可见子图2(b)的块效应最突出，子图2(d)基本不存在块效应。而子图2(b)、图2(e)和图2(f)是步长相同(均为λ=16)，不同子块大小下的POSHE算法增强后的块效应程度，可见图2(b)图的块效应最突出，图2(f)最弱。由此表明:在块大小一致的情况下，步长越大，块效应越突出;在步长一致的情况下，块越小，块效应越突出。

图2 POSHE算法仿真分析

2．2 增强效果与子块大小和步长的关系

对比子图2(b)、图2(e)和图2(f)，子图2(b)远处事物细节最明确，边缘最清晰，但近处事物过增强现象最严重，如大楼位置处，同时天空背景也被增强，如图像中上部分区域，突出表现为噪声，子图2(e)次之，子图2(f)视觉效果最好，但远处细节的凸显效果不如子图2(b)。比较子图2(b)、图2(c)和图2(d)，三者增强的效果一致，均出现过增强现象。由此表明增强效果与子块大小有关，子块大，增强图像灰度分布均匀平滑，但远处事物细节不明确，子块小，远处事物细节明确，但近处事物出现了过程强现象;增强效果与步长关系不大。

综上所述，采用POSHE算法对图像增强处理后，块效应程度、增强效果与子块大小和步长有着密切的关系。然而，针对不同场景图像，要达到同样的增强效果和较弱的块效应，子块大小和步长的取法往往不一样。所提算法摒弃了对子块大小和步长的过度依赖，在子块大小和步长一定的情况下，能取得较好的增强效果，充分抑制块效应、消除过增强现象。

3 限制对比度的多层POSHE算法(CLMPOSHE)

CLMPOSHE算法先对每个子块作限制对比度直方图均衡(contrast limited histogram equalization，CLHE)，再将改进的多层POSHE处理结果加权融合，处理后图像不仅具有良好的灰度分布、鲜明的局部细节还拥有丰富的边缘信息，且块效应也能得到充分抑制。

3．1 POSHE过增强的产生原因及解决方案

直方图均衡处理的对比度增强程度与累加直方图的斜率成正比，GHE由于过度拉伸图像对比度产生过增强现象，即累加直方图曲线过于陡峭，由此通过设定阈值限定每个灰度级拥有的像素数目抑制过增强现象。图3为限制对比度直方图均衡的实验仿真，其中阈值设定为每个灰度级所占像素平均数目的1．5 倍。

图3 限制对比度的直方图均衡仿真

上述仿真验证截取直方图是一种限制对比度增强幅度的有效方法。图3(e)中截取后的累加直方图(虚线)的累加函数曲线斜率明显小于原累加直方图(实线)，即对比度增强幅度较小(灰度值［0，49］以及［225，255］中二者斜率关系相反，究其原因原图像灰度范围在［50，224］，此区间之外累加直方图保持不变)，图3(c)不存在过增强现象，即天空区域无光晕效应、图像左下角凸显部分细节信息，由于CLHE从全局角度出发，所以局部增强效果不是很理想。

3．2 POSHE块效应的产生原因及解决方案

POSHE方法是在部分重叠子块中作均衡处理，各个子块的灰度分布不同，在子块边缘会产生明显的灰度不连续现象，即方块效应，简称块效应(Blocking Effect)，如图4所示。

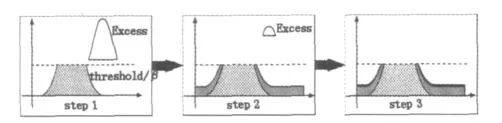
图4 直方图截取再分配过程

块效应方格尺寸即为POSHE算法参数的步长，采取多层POSHE融合策略抑制块效应是一种简单有效的方法［6］，大子块、大步长处理只存在轻微的块效应，小子快、小步长则会带来严重的块效应，后者的块效应区域恰好是前者的平滑区域，二者融合可以减弱块效应，而对图像的清晰度影响甚小。

3．3 对比度限制

在每层POSHE处理前，先对其各子块的直方图截取然后均匀分配到各灰度级上，通过限制其直方图高度降低累加直方图曲线的斜率，即降低对比度增强幅度，从而限制噪声放大及局部过增强现象。分配过程如图4所示，对于nbits灰度图像，定义任意N×N像素子块中每个灰度级拥有的像素平均数目为α，即 α=N×N/2n，直方图像素分配步骤如下［7］:

(1)如果h(i)≥β，i=0，1，…，2n－1，则h(i)=β，Excess=Excess－β+h(i)，h(i)为灰度级i的像素个数，阈值β为单个灰度级拥有像素个数的上限，Excess为超过β的像素数目总和;

(2)如果h(i)＜ β － β/2n，i=0，1，…，2n－1，则h(i)=h(i)+β/2n，Excess=Excess－β/2n;

(3)如果 β ＞h(i)＞β －β/2n，i=0，1，…，2n－1，则h(i)=β，Excess=Excess－β+h(i);

(4)通过上述三步处理之后，如果Excess＞0且h(i)＜β，i=0，1，…，2n－1，则h(i)=h(i)+1，Excess=Excess－1，直到Excess=0为止。

采用固定阈值β并未考虑子块的局部特征，针对大小不同的子块，应当自适应地选取β，显然β的下限是α，当β＞5α时，对比度限制能力较弱，图像逐渐出现噪声放大和过增强现象，所以拟定β∈［α，5α］。大子块处理为了获得符合人类视觉的图像，β应当较小，即不会使得某些灰度级占有过多的像素，从而使得直方图灰度分布均匀，图像不会过亮或过暗;适中子块处理目的在于增强局部细节，β偏小，均衡处理不能很好的凸显细节，而β偏大，又会出现过增强现象，场景中的事物表现的不自然，所以β的选取应当适中;小子块处理旨在锐化降质图像中模糊的边缘，β应当较大，如果过度限制子块的单个灰度级像素的数目，局部对比度无法充分拉伸，不能充分锐化图像。

3．4 多层POSHE自适应融合

3．4．1 融合方式

对多层POSHE处理结果常见的融合方式有:等比例融合，基于全局图像质量评价的自适应加权融合。

(1)等比例融合。将每一层处理处理的结果以相同的系数融合，即，其中Pj为第j层POSHE处理的结果，n为处理的层数，Po为处理后的图像。

(2)基于全局图像质量评价的自适应加权融合。选择合适的图像质量评价指标，对每层POSHE处理后图像的质量进行评估，以各层指标之间的比例作为融合的系数，其中wi其中为归一化的评价指标满足为第j层POSHE处理的结果，n为POSHE处理的层数，Po为处理后的图像。

上面提及的两种融合方式，等比例融合没有考虑到每层POSHE处理后图像的质量，如果某一层POSHE处理后图像质量较差，却赋予和其他层相同权值，势必会影响到融合后图像的整体质量;而基于全局图像质量评价的自适应加权融合弥补了等比例融合的不足，某一层增强的效果较好，该层则会获得较大的权值，这对于增强的最终结果是比较有利的，但质量评价仅从全局角度出发，忽略图像局部特征，局部细节表现方面有待提高。

3．4．2 基于子块图像质量评价的自适应融合

如果图像中存在大面积的背景区域，小子块POSHE处理会将这些背景区域分成小的子块进行均衡，这自然没考虑到该区域的整体灰度分布，所以此时大子块处理会获得良好的局部效果，即每一层子块的权值与局部特征息息相关，所以选择基于子块图像质量评价的融合方式。

首先要确定一个常用的、稳定的无参考图像质量评价指标，图像信息熵(information entropy)可以衡量图像信息内容的多少［8］，图像内容越丰富，信息熵越大，反之亦然。对于nbits灰度图像，信息熵的定义如下:

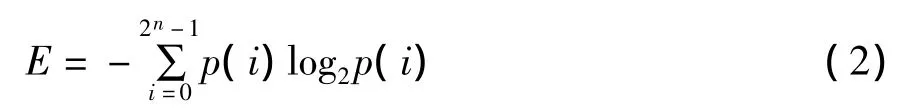
其中，p(i)为灰度级为i的像素出现的概率。然后给出图像基于子块质量评价融合的公式:

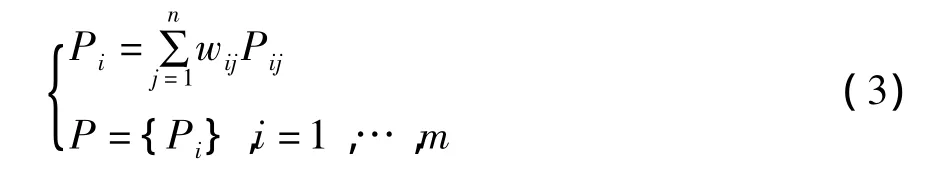
其中，Pi为子块i融合后的图像;Pij为子块i第j层的POSHE处理结果;n为POSHE处理层数;P为处理最终结果;m为图像划分子块个数;wij，j=1，2，…，n为子块i第j层POSHE处理后的加权系数，满足:

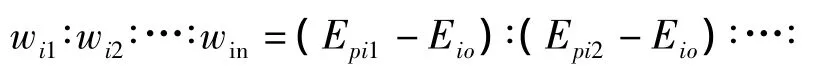
4 仿真实验与分析

本算法在 Intel Core4 Xeon CPU E5507，主频2．27 GHz，2．99 G 内存的计算机 Matlab2007a 平台上实现，所选图像为512×512×8 bits灰度图像，所选视频为512×512×8 bits灰度航拍视频，帧频为25 fps，采用三层POSHE处理，每层POSHE算法的子块大小分别选为图像尺寸的1/2、1/4和1/8，较小的步长可以有效平滑块效应，但如果步长太小，会大大增加算法时间复杂度，然而块效应抑制效果不再明显提高，因此步长选为每层子块的1/16，既可较好的平滑块效应，又可获得较低的时间复杂度，大子块、中子块和小子块的阈值分别选为2α，3α和4α(α的定义见第3．3节)，融合的子块大小为图像尺寸的1/2，POSHE算法子块大小为128，步长为8。

4．1 图像仿真结果与分析

图5(a)和图5(d)分别为原始雾天测试图像，POSHE处理后，图5(b)和图5(e)的天空区域中出现明显的块效应和过增强现象，经过本文方法处理，有效增强其对比度和纹理，图5(c)和图5(f)层次分明，显示了较好的去雾效果。

图5 典型图像增强效果第一列:原始的雾天图像;第二列:POSHE增强效果;第三列:本文方法增强效果

4．2 视频仿真结果

对比图6(a)和图6(b)的增强效果，增强前图像近处画面模糊不清，图像远处画面缺乏层次，丢失很多细节，本文方法增强后图像远处细节得到凸显，整体画面非常清晰，具有真实自然的视觉效果。

图6 视频增强效果图

5 结论

本文提出了一种限制对比度的多层POSHE自适应图像增强算法，将对比度限制引入POSHE方法中，结合多层融合处理消除了POSHE方法中存在的块效应和过增强现象，针对雾天不同退化程度的低照度图像，本文方法能够有效增强其对比度和局部信息，在亮度、对比度和细节方面都能取得较好的视觉效果。基于局部直方图均衡的图像增强方法具有自适应好、易于并行实现以及鲁棒性强的优点，因此本文提出的方法具有一定的通用性，在视频监控、目标识别和图像制导等实时图像处理领域有较高的工程实用价值。

［1］ R C Gonzales，R EWoods．Digital image processing［M］．2nd ed．Beijing:Publishing House of Eletronic Industry，2007．

冈萨雷斯．数字图像处理［M］．2版．北京:电子工业出版社，2007．

［2］ Chen Zheng，Ji Shupeng．Enhancement algorithm of infrared images based on Otsu and platear histogram equalization［J］．Lasers ＆ Infrared，2010，40(4):438 － 441(in Chinese)

陈峥，吉书鹏．一种基于Otsu法和平台直方图均衡的红外图像增强算法［J］．激光与红外，2010，40(4):438－441．

［3］ V T Tom，G JWolfe．Adaptive histogram equalization and its applications［J］．SPIE Applicat．Dig．Image Process．IV，1982，359:204 －209．

［4］ JY Kim，L SKim，SH Hwang．An advanced contrast enhancement using partially overlapped sub-block histogram equalization［J］．IEEE Transactions on Circuits and Systems for Video Technology，2001，11(4):475 －484．

［5］ Zhai Yishu，Liu Xiaoming，Tu Yayuan，et al．An improved fog-degrade image clearness algorithm［J］．Journal of Dalian Maritime University，2007，33(3):55 －58(in Chinese)

翟艺书，柳晓鸣，涂雅瑗，等．一种改进的雾天降质图像的清晰化算法［J］．大连海事大学学报，2007，33(3):55－58．

［6］ Nicholas Sia Pik Kong，Haidi Ibrahim．Multiple layers block overlapped histogram equalization for local content emphasis ［J］．Computer and Electrical Engineering，2011，(37):631 －643．

［7］ Kentaro Kokufuta，Tsutomu Maruyama．Real-time processing of contrast limited adaptive histogram equalization on FPGA ［C］．International Conference on Field Programmable and Applications，2010:155 －158．

［8］ Xie Z X，Hu Q，Wang Z F，et al．A NR-IQA based on product of information entropy and contrast［J］．International Symposium on Information Science and Engineering，2008:608 －611．