印度尼西亚近海潮汐潮流的数值模拟

滕 飞，方国洪,王新怡，魏泽勋，王永刚

(1. 国家海洋局 第一海洋研究所，山东 青岛 266061;2. 海洋环境科学和数值模拟国家海洋局重点实验室，山东 青岛 266061)

潮汐是海洋中最重要的现象之一，而印度尼西亚的潮汐现象在海洋中是最复杂的。复杂的沿岸地形、狭窄的海峡和无数的小岛屿、广阔的大陆架以及迅速变化的水深，再加上从印度洋和太平洋传入的巨大的潮汐能量，这些组成了一个复杂的潮汐系统。印尼海中有多个无潮点，海峡的潮流流速大。潮汐对印尼海的海水混合和环流有很大影响。

早在1981年，Webb[1]模拟了卡奔塔利亚湾和阿拉弗拉海的潮汐；1993年，Wolanski[2]模拟了卡奔塔利亚湾的潮汐；1996年，Hatayama等[3]计算了整个印尼海的M2和K1分潮。2002年，Egbert等[4]将卫星高度计同化到动力学模式中，给出了印尼海的正压潮。根据这个结果，于2005年，Ray[5]对印尼海域潮汐作了详细的阐述。2008年，Koropitan和Ikeda[6]模拟了爪哇海的潮汐环流及混合。

前人对于印尼海及其周边海域的水动力模拟研究均采用矩形网格进行计算。采用目前较为流行的有限体积近岸海洋模式FVCOM[7]，该模式采用非结构三角形网格，对印尼海主要的岛屿、海峡等地形变化剧烈地方进行加密处理，大大提高了海洋模式对复杂海岸线的拟合程度。模式采用干-湿网格判别技术较好地处理了模型的固体边界，考虑地转科氏力、非线性效应、水平对流扩散等，建立了分辨率比较高的印尼海及其周边海域的数值模式。模拟结果与前人的结果相比较有所改进。根据模式结果，本文给出了印尼海主要的4个分潮(M2，S2，K1，O1)的同潮图，并分析了印尼海及其周边海域的潮汐、潮流的分布特征和潮波的传播特征。

1 计算方法与计算过程基本方程组

1.1 基本方程组

FVCOM模式采用σ垂向坐标来模拟不规则的底部地形，坐标变换公式如下：

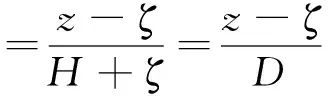
(1)

由于计算范围大，考虑纬度不同所引起的科氏力的变化，采用球坐标连续方程，球坐标系下的σ坐标的连续方程、动量方程和状态方程如下：

(2)

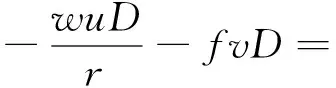
(3)

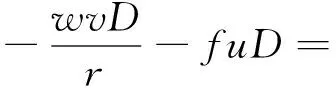
(4)

(5)

式中，t为时间；r为地球半径；λ为计算点经度；φ为计算点纬度；σ为垂向分层(海表面为0，海底为-1)；H为未扰动水深；ζ为相对于未扰动海面的潮汐高度；D为扰动水深；u，v，ω分别为东向，北向和垂直速度；ρ为海水密度；f为科氏参数；g为地球重力加速度；Km为垂直混合参数；Fu和Fv为水平动量的扩散项。

在大范围的区域中，引潮势产生的平衡潮是不能忽略的，因此整个模拟过程必须包括引潮力。对于半日潮来说，引潮势为

βiAicos2φcos(ωit+2λ)

(6)

对于全日潮，引潮势为

βiAisin2φcos(ωit+λ)

(7)

式中，Ai和ωi为第i个分潮的振幅和频率；Nsemi和Ndiurnal为模式中参与计算的半日潮和全日潮的个数；βi可表示成：

βi=1+klove-hlove

(8)

式中，k和h为love数。在FVCOM中，各个分潮的klove和hlove所采用的数值见表1。

表1 模式中各分潮love数klove和hloveTable 1 Love numbers klove and hlove for the tidal constituents in model

1.2 模式水深的确定

在潮汐模拟中，水深是至关重要的参数。但是我们发现，现有的格点化水深数据etopo1(1′分辨率)和etopo5(5′分辨率)在印尼近海深水区一致性较好，而在浅海区则差别较大，而且两者与海图资料都不相符。我们通过多次试验，最后确定了本研究采用的水深数据。在深海等大部分海域采用etopo1的数据，在纳土纳海和爪哇海采用从海图读取的水深数据，在阿拉弗拉海从131°E到135°E用etopo1和etopo5的数据进行过渡，在卡奔塔利亚湾中采用etopo5的数据，模式中采用的水深分布见图1。

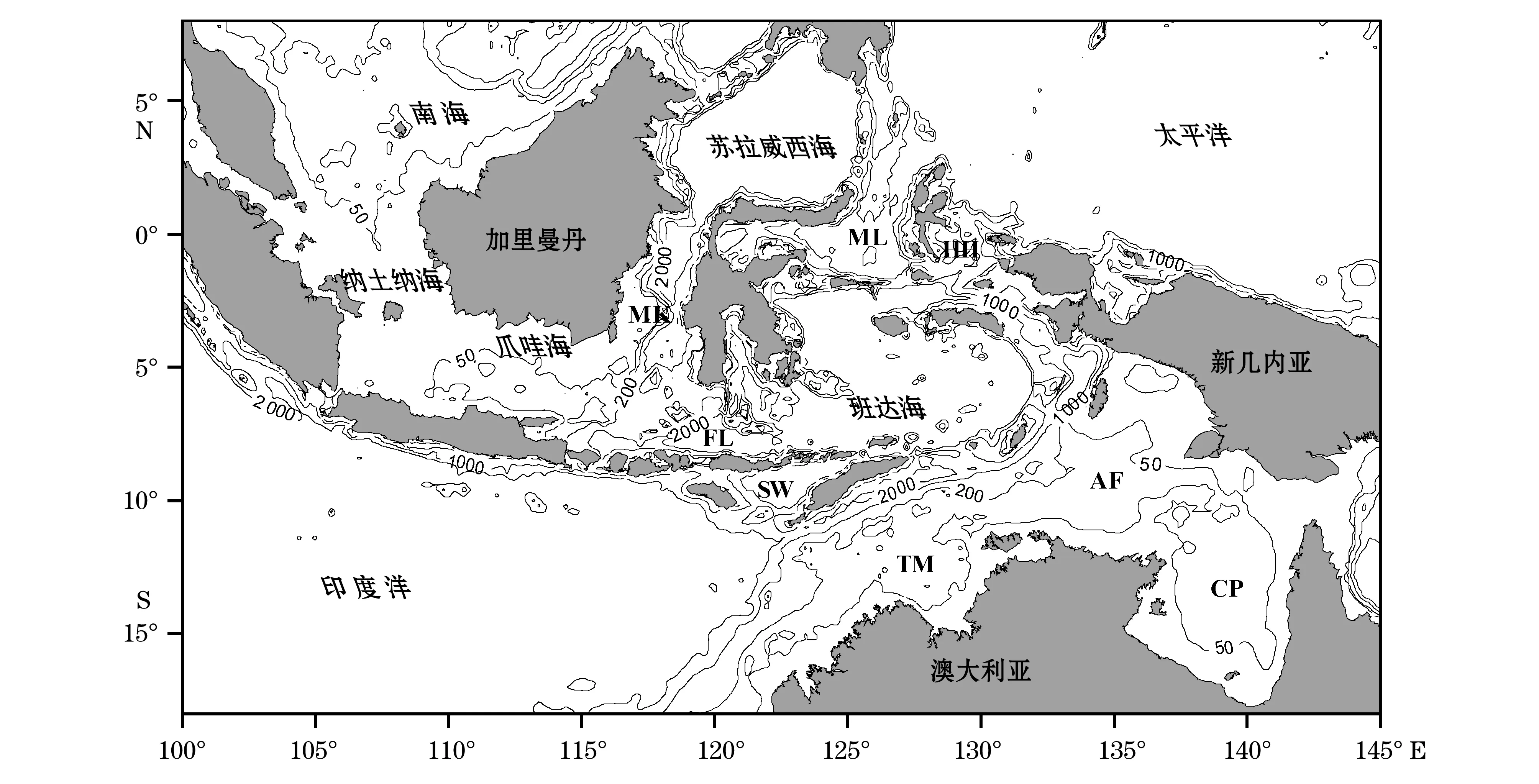
MK-望加锡海峡，ML-马鲁古海，HH-哈马黑拉海，FL-弗洛勒斯海，SW-萨武海，TM-帝汶海，AF-阿拉弗拉海，CP-卡奔塔利亚湾

1.3 计算海区、边界条件的选取与计算过程

本研究海区为从16°S～8°N，100°～145°E的印尼近海(图1)，但数值计算区域较大，包括印度尼西亚内部和周边海域、南海大部(包括泰国湾)、印度洋东北部、太平洋西南部以及澳大利亚北部的卡奔塔利亚湾(图2)。计算网格水平分辨率在印尼海域岛屿平均为1/12度，在大陆边界平均为1/5度，在开边界平均为1/2度。共包含80 096个网格节点，155 977个三角单元(图2)；垂向分6层。FVCOM模型采用内外模分离的方式求解，二维外模数值格式是基于三角形网格的有限体积法，将连续方程和动量方程在三角形单元内积分后，通过改进的四阶龙格库塔方法求解。三维内模的动量方程采用简单的显式和隐式相结合的差分格式求解，时间步长外模为6 s，内外模时间步长比率为10。

计算的初始条件假设海洋是静止的，海表面的扰动水位初始全部为0，所有三角形网格中心点的流速u=v=0。本文采用正压模式，取整个海域内的温度和盐度均为常数，温度为18 ℃，盐度为35.0。在南海、印度洋、太平洋共设有4个开边界，开边界上每个点的水位给定，由T_tide的预报程序给出[8]，其中M2，S2，K1和O1调和常数来自DTU10[9]数据。

图2 计算网格Fig.2 Computation grids

模式运行30 d。对后15 d时间序列进行调和分析，得到网格点上的水位的调和常数、每个三角形中心点的潮流椭圆要素以及速度各分量的调和常数。

2 计算结果与实测结果的比较

2.1 评价方法

为了比较模式的结果，我们用TOPEX/Poseidon(T/P)卫星数据和地面验潮站数据分别与模式结果进行比较验证。下面介绍几种比较常用的计算值与观测值之偏差不同的度量方法[10]。首先是一种较直观的方法，分别是振幅之间和迟角之间的均方偏差：

(9)

(10)

式中,H和G分别为分潮的振幅和迟角，下标a和b分别为模式结果和观测结果；K为比较的站位总个数。这种方法比较直观，但是当H较小时，G的计算和观测值都不稳定，同时,H比较小时,G的误差对潮高误差影响也较小，因此在无潮点附近迟角很容易出现较大的误差，因此不考虑H的差别而将所有迟角差值的平方进行平均具有相当大的偶然性。另一种方法是考察潮高之差的均方根。观测站潮高的均方根值为

(11)

观测潮高和模式潮高之差的均方根为

(12)

相对偏差：

k=RMSd/RMSh

(13)

2.2 与T/P卫星数据的比较

为对模式结果的准确度进行评估，我们选用T/P卫星轨道交叉点的调和常数对模式结果进行验证。由于在陆地边缘的结果有误差，我们对落在模式计算范围内的所有T/P交叉点数据中剔除了几个岛屿附近的数据。实际采用的比较站位共104个，其分布图见图3。表2为模式数据与T/P卫星数据的振幅之间和迟角之间的均方偏差，潮高之差的均方根以及相对偏差。

图4和图5分别给出在T/P交叉点上计算和T/P观测所得的M2和K1分潮振幅和迟角的相关关系图。图中RMS值与表2相同。r为模式值和观测值的相关系数。

图3 T/P轨道交叉点站位Fig.3 Positions of the TOPEX/Poseidon crossover points

表2 模式结果与T/P卫星轨道交叉点观测值比较Table 2 Comparison of the model results to the observations at TOPEX/Poseidon crossover points

图4 M2分潮模式结果和卫星数据的相关性Fig.4 Correlation between the model results and the T/P data for M2

图5 K1分潮模式结果和卫星数据的相关性Fig.5 Correlation between the model results and the T/P data for K1

2.3 与验潮站数据比较

本文的验潮站取自国际水文组织IHO潮汐调和常数数据集，共选取其中79个站位(图6)。挑选的原则是用于分析调和常数的观测时间大于25 d，并且较均匀分布在研究区域内。用验潮站数据与模式结果进行了对比，比较结果见图7、图8。模式数据与验潮站数据的振幅之间和迟角之间的均方偏差，潮高之差的均方根以及相对偏差见表3。

图6 验潮站站位Fig.6 The positions of the tide gauge stations

表3 模式数据与验潮站数据比较Table 3 Comparison of the model results to the data from tide gauge

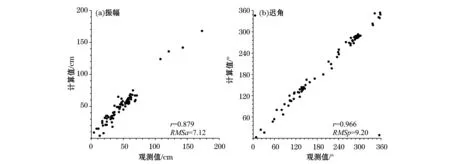
图7 M2分潮模式结果和验潮站数据的相关系数Fig.7 Correlation between the model results and the tidal gauge data for M2

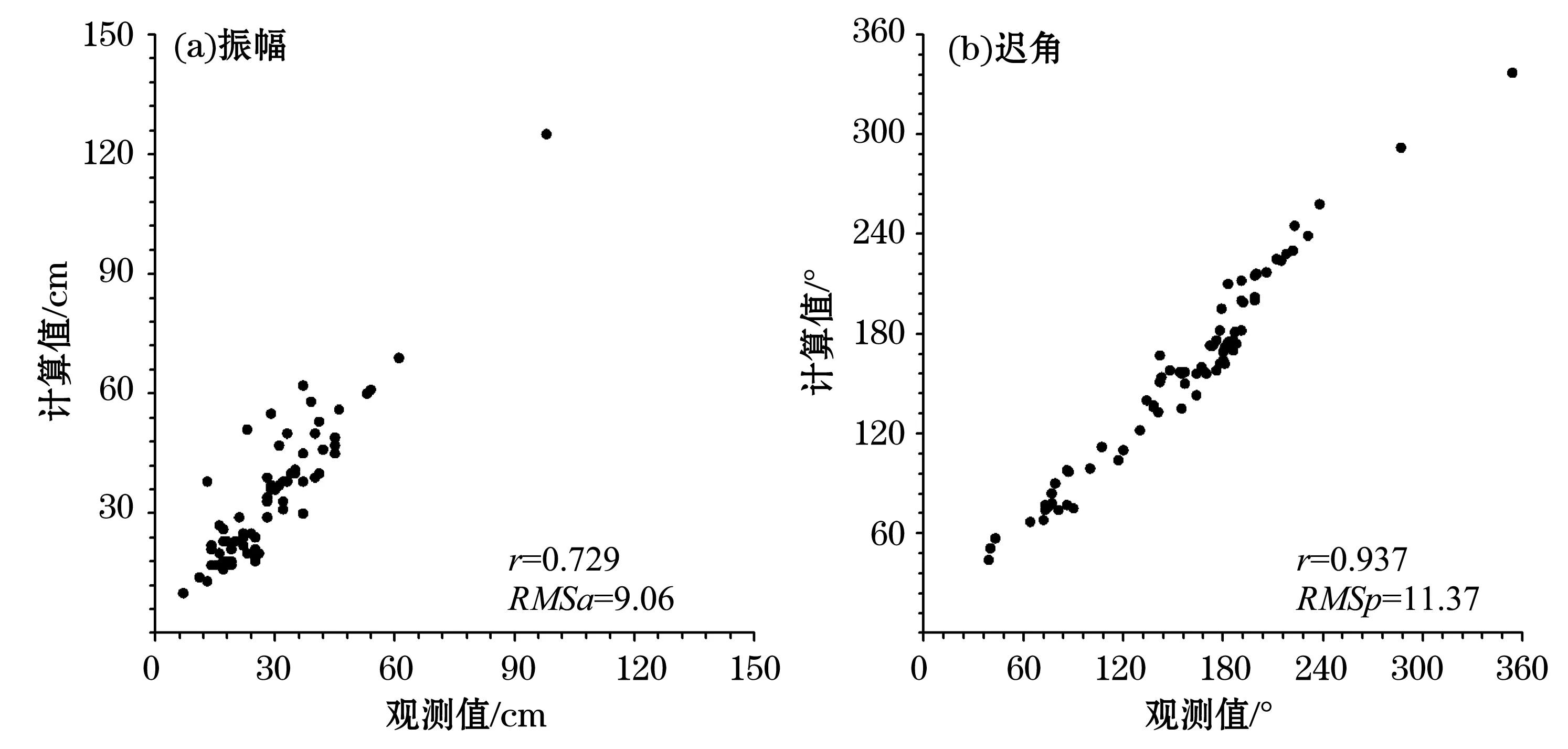
图8 K1分潮模式结果和验潮站数据的相关系数Fig.8 Correlation between the model results and the tidal gauge data for K1

从表2和表3来看，模式结果与T/P结果比较一致，振幅均方根差大约为2～5 cm，迟角均方根偏差大约为5°～8°，潮高的均方根偏差大约为2～4 cm，相对偏差为0.11～0.19。模式结果与验潮站结果的偏差大一点，振幅均方根偏差为4～9 cm，迟角均方根偏差为9°～12°，潮高的均方根偏差为4～8 cm，相对偏差为0.2～0.3之间。模式和验潮站观测结果偏差较大是由于验潮站大多位于港口内部，局地效应不能很好地在大范围数值模式中考虑。但总的来看模式和观测值有较好的一致性。特别与Hatayama等[3]的图4和图14比较，可以看到本文结果更符合观测值。

3 印尼海及其周边海域的潮波分布

3.1 潮汐分布

模式计算所得到的4个分潮的同潮图见图9。M2分潮最大振幅出现在澳大利亚西北海域，其值可超过3 m。次大值出现在加里曼丹岛西北岸，其值超过1.5 m，与Fang等[11]的南海潮汐数值模拟结果一致。印尼海大部海域M2分潮振幅都不大，在0.6 m以下。在澳大利亚的西北海域约瑟夫-波拿巴湾西北口有一个顺时针的无潮点，在阿拉弗拉海的北部有一逆时针无潮点。在南纳土纳海、爪哇海到弗洛勒斯海一带M2存在多个无潮点，振幅非常小。

……为振幅/cm；——为迟角/°

S2分潮的分布特征与M2相近(图9a,b)。在南纳土纳海、爪哇海至弗洛勒斯海一带也与M2一样存在多个无潮点，振幅很小，但是无潮点的位置与M2有些不同。另外，值得特别注意的是，在望加锡海峡，M2的迟角从南向北推迟，而S2的迟角反过来从北向南推迟。

K1分潮振幅较大值出现在南海南部、纳土纳海南部、爪哇海东北部、阿弗勒斯海北部和约瑟夫·波拿巴湾，其中尤以阿弗勒斯海北部的新几内亚西南沿岸为最大，可超过1.2 m(图9c)。卡奔塔利亚湾有一个顺时针旋转的无潮点，西爪哇海有一个同潮时线密集的波节带，但似乎未能形成无潮点。

O1分潮的分布特征与K1相近，其振幅大约为K1的2/3左右。卡奔塔利亚湾口也有一个无潮点，西爪哇海也存在一个波节带，这里是否形成无潮点还难以确定。

图10为潮汐类型图。由于印尼海域半日潮波结构复杂，一些区域(特别是M2无潮点附近)S2分潮振幅可能大于M2，本文采用F=(HO1+HK1)/(HM2+HS2)的计算结果作为潮汐类型的判断参数。按照国外的习惯，F=0～0.25为半日潮类型，F=0.25～1.5为半日为主的混合潮汐类型，F=1.5～3为全日潮为主的混合潮类型，F>3.0为全日潮类型。从图中可以看出,在马来半岛以东海域、纳土纳海南部(包括卡里马塔海峡)、爪哇海东部、新几内亚岛西南外海及卡奔塔利亚湾东南部为规则全日潮。其它海域大部分为混合潮。半日潮类型只出现在澳大利亚西北近岸海域。

图10 潮汐类型分布图Fig.10 Distributions of tide types

3.2 潮流分布

为了研究印尼海区域的潮流分布情况，分别计算了4个分潮的潮流椭圆要素(长轴、短轴、倾斜角、格林威治迟角)，其中M2和K1分潮的潮流椭圆分别见图11和图12，阴影海域部分代表潮流以逆时针方向旋转，无阴影海域部分为顺时针旋转。

对于M2分潮来说，在连接太平洋和爪哇海东北部的望加锡海峡、马鲁古海、哈马黑拉海以及斯兰海潮流呈现往复流，流速比较大，其中在马鲁古海与班达海之间的个别海峡中最大流速可以超过100 cm/s。而在班达海和苏拉威西海中部的深水区域潮流非常小，都小于11 cm/s。在爪哇海的内部水深较浅，流速较强，其中在爪哇海东南部最大可以达到51 cm/s。卡奔塔利亚湾水深较浅，在该湾东北部流速最大可达80 cm/s，这个区域的S2分潮与M2相比除流速偏小以外，分布特征基本一样。

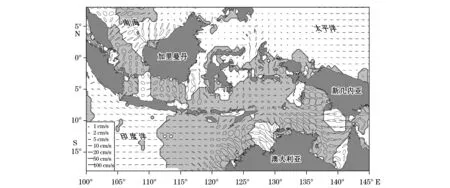
图11 M2分潮潮流椭圆Fig.11 M2 current ellipses

对于K1分潮而言，在纳土纳海南部及卡里马塔海峡附近的流速呈现往复流，流速较大，最大流速出现在卡里马塔海峡西部海峡中。在爪哇海呈现东西的往复流，流速大约在30 cm/s左右，最大流速出现在爪哇海的西北部。在班达海和苏拉威西海水深较深地方的流速较小。在望加锡海峡、马鲁古海、哈马黑拉海以及斯兰海中流速比M2分潮的流速小。在卡奔塔利亚湾的K1分潮流基本上都按顺时针方向旋转，特别在湾口，旋转特性明显。O1分潮的分布情况与K1分潮相似，只是流速较小。

图12 K1分潮潮流椭圆Fig.12 K1 current ellipses

为了对印尼近海潮流的大小有一个总体的了解，图13给出了4个主要分潮最大流速之和的分布。由图可以看出，强的潮流主要出现在陆架浅水区和狭窄的海峡中。

图13 M2、S2、K1和O1分潮最大流速之和(单位：cm/s)Fig.13 Sum of the maximum current speeds of M2, S2, K1 and O1 (unit: cm/s)

3.3 潮余流分布

由4个分潮共同引起的欧拉潮余流分布图见图14，在卡奔塔利亚湾中潮余流呈现非常规律的顺时针环流。在澳大利亚西北部潮余流很强，达到将近4 cm/s。在纳土纳海西部沿岸区域存在比较弱的由北向南的余流。

图14 潮余流分布图Fig.14 Distributions of tidal residual currents

图15 M2，S2，K1和O1分潮能通量密度分布图Fig.15 The energy flux density vectors of tidal constituents M2, S2, K1 and O1

4 潮能通量和潮波传播

潮能通量强度又叫做能通量密度，即单位时间通过自海底至海面单位宽度断面的潮能通量，其计算公式为

(14)

式中，v和ø分别为流速和能通强度向量；T为潮波周期；ρ为海水密度，本文取1 025 kg/m3；h为当地水深。式(14)对各分潮求时间平均，可得[12]：

ρghHUcos(G-ξ)

(15)

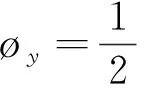
(16)

式中，øx和øy分别为潮能通量密度的东向分量和北向分量；H和G分别为水位的调和常数；U、ξ和V、η分别为潮流东向和北向分量的调和常数。

Ray[5]曾给出印尼海M2和K1分潮潮能通量的输送特征。由于他采用了统一的线性比例尺，许多潮能通量较弱的海区如纳土纳海和爪哇海都未能给出。本文根据式(15)和(16)计算了M2，S2，K1和O1分潮的潮能通量，见图15。为了显示潮能通量区域的特征，图中矢量的长度取与能通量的平方根成正比例，其大小比例尺见图的左下方。

从半日潮M2分潮来看，潮能主要是由印度洋进入印尼海和卡奔塔利亚湾，其中部分能量穿过望加锡海峡、马鲁古海和哈马黑拉海后进入太平洋。南海有能量向南传输，但只能影响到纳土纳海，爪哇海的M2分潮主要还是依靠印度洋来的能量来维持。S2分潮能量在大部分区域与M2分潮相同，也是由南向北输向太平洋。与M2分潮不同的是在望加锡海峡潮能由北向南进入印尼海域，而M2分潮的潮能输送方向是由南向北进入苏拉威西海，进而进入太平洋。

在印尼海域全日潮能量传输与半日潮正好相反，K1和O1分潮的潮能是由太平洋通过印尼各海域输向印度洋和卡奔塔利亚湾。来自南海的潮能基本上只到达卡里马塔海峡附近，爪哇海的全日潮运动主要依靠来自太平洋，通过望加锡海峡的潮能来维持。

5 结 语

基于FVCOM海洋数值模式，本研究采用非结构三角形网格对计算海域进行分辨率的调整，应用有限体积法对原始方程进行离散求解，建立了印尼海及其周边海域的潮汐、潮流数值模型，并与T/P卫星数据和验潮站数据进行比较，结果良好。用该模式结果进行了印尼海域的潮汐类型，潮流和潮能的分析。

与Hatayama等[3]的结果相比，本文结果与实测符合程度有显著提高。但是由于印尼近海岛屿众多，潮波结构复杂，本研究尚有待进一步改进。一个有效的方法是将印尼近海划分为若干个海区分别进行模拟。

参考文献(References):

[1] WEBB D J. Numerical model of the tides in the Gulf of Carpentaria and the Arafura Sea[J]. Marine & Freshwater Research, 1981, 32(1): 31-44.

[2] WOLANSKI E. Water circulation in the Gulf of Carpentaria [J]. Journal of Marine Systems, 1993, 4(5): 401-420.

[3] HATAYAMA T, AWAJI T, AKITOMO K. Tidal currents in the Indonesian Seas and their effect on transport and mixing [J]. Journal of Geophysical Research, Ocean,1996, 101(C5):12353-12373

[4] EGBERT G D, EROFEEVA S Y. Efficient inverse modeling of barotropic oceantides [J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2):183-204.

[5] RAY R D, EGBERT G D, EROFEEVA S Y.A brief overview of tides in the Indonesian Sea [J]. Oceanography, 2005,18(4):74-79.

[6] KOROPITAN A F, IKEDA M. Three-dimensional modeling of tidal circulation and mixing over the Java Sea [J]. Journal of Oceanography, 2008, 64(1): 61-80.

[7] CHEN C S, BEARDSLEY R C, COWLES G. An unstructured grid, finite-volume coastal ocean model FVCOM user manual [R]. North Dartmouth: UMASSD, 2006:6-8.

[8] PAWLOWICZ R,BEARDSLEY B,LENTZ S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE [J]. Computers and Geosciences, 2002, 28(8):929-937.

[9] CHENG Y C, ANDERSEN O B.Multimission empiricalocean tide modeling for shallow waters and polar seas [J]. Journal of Geophysical Research, Ocean(1978-2012),2011, 116(C1):1001-1011.

[10] WANG Y H, FANG G H, WEI Z X, et al. Accuracy assessment of global ocean tide models base on satellite altimetry [J]. Advances in Earth Science, 2010, 25(4):353-359.

[11] FANG G H, KWOK Y K, YU K, et al. Numerical simulation of principal tidal constituents in the South China Sea, Gulf of Tonkin and Gulf of Thailand [J]. Continental Shelf Research, 1999, 19(7):845-869.

[12] FANG G H. A Two-Dimensional Numerical Model for Tidal Motioninthe Taiwan Strait [J]. Marine Geophysical Research, 1984, 7(1-2): 267-276.