CPV(1)分段法在间歇过程中的应用
袁 杰,郭小萍,刘如有,李 元
(1.沈阳化工大学 信息工程学院,辽宁 沈阳 110142;2.中国市政工程东北设计研究总院,吉林 长春 130021)
近几年化工产品市场品种更新迅速,需求不断变化,间歇过程的灵活性能适应小批量、高附加值、多品种的工业要求.因此,间歇过程将成为化工生产的重要方式.动态特性是间歇过程的本质.间歇过程本身具有多工况、分阶段、阶段时长不一致等特点,产品质量很容易受到外部不确定因素的影响.这些特点使间歇过程的故障检测更加复杂.
针对间歇过程的故障诊断,多向偏最小二乘法[1](MPLS,Muti-way partial least squares)和多向主元分析[2-3](MPCA,Muti-way principal component analysis)是最常用的方法.MPCA 最早是由Nomikos 和Macgregor 在1995 年应用到间歇过程故障诊断中的,达到了很好的检测和诊断目的.然而,间歇过程中存在多个操作阶段,各个阶段内部可能具有其他阶段不具有的性质.从统计学角度分析,不同阶段的数据特征可能存在很大差距.在间歇过程故障诊断中,如果统一建模,某些总体的信息可能掩盖了局部阶段内的信息变化.所以,批次过程的分段故障检测成为一个研究热点.目前,将间歇过程合理划分为不同时段的方法有很多,最常用方法是自动识别算法[4],该方法通过某种算法程序能够自动识别出过程中的各个阶段.文献[5-7]属于自动识别算法的应用,从主元累计贡献率的角度进行了阶段划分和故障检测的探究.本文在将检测数据等长处理后,进行主元分析[8],采用第一主元贡献率(CPV(1))的变化来判断原数据是否分段,也属于自动识别算法.仿真结果表明:使用第一主元贡献率的变化能准确反映生产阶段的变化.
1 间歇过程的数据处理方法
1.1 轨迹同步化
间歇过程的时变特点使得间歇过程所采集的数据呈现批次数据轨迹不等长的特点,因此,批次过程的轨迹同步化处理十分关键.此处理目的是将不等长的数据处理为便于操作的等长数据.目前比较常用的轨迹同步化处理方法有:最短长度法、指示变量法(indicator variable technique,IVT)等.
(1)最短长度法
最短长度法以间歇操作数据最短的批次做为基准,其余批次的数据截取长度与基准批次相同.这种方法一方面要求在公共部分的过程变量轨迹保持一致,另一方面公共时间段内要包含间歇过程的主要操作,在超出基准长度的时间位置包含的都是数据中次重要信息.
(2)指示变量法[5]
通常情况下,间歇过程变量都对应着时间而改变,但是如果以其他的变量来替代时间,就可以对不等长数据进行同步处理.把可以用来代替时间的变量命名为“指示变量”.这种方法的思想是用指示变量的进程来代替时间,将其余变量进行重新采样,是一个数据插值过程.
文中青霉素仿真数据的轨迹同步化采用的是指示变量法,半导体数据采用的是最短长度法.
1.2 数据展开
经过轨迹同步化之后的数据是三维数据,在采用主元分析之前,需要将其展开为二维数据.传统的展开方式有以下两种:基于变量的展开和基于批次的展开.这两种展开方式如图1 所示.

图1 批次过程的展开方式Fig.1 The unfolding means of data
两种数据展开方式都是针对采样时刻片进行的操作.基于变量的展开方式是将每个采样时刻片展开为(I×K)×J 的矩阵.基于批次的展开方式是将采样时刻片展开为I×(J ×K)的矩阵.一般的,根据数据展开后的操作区分,在建模和检测时采用基于批次的展开方法,在数据分段时采用基于变量的展开方式.
2 基于第一主元贡献率差值变化的批次分段
2.1 主元分析方法
主元分析(PCA)是多元统计分析中最基本的方法之一.假设x ∈Rm,代表一个包含了m 个传感器测量样本,每个传感器个有n 个独立采样,构造如下的测量数据矩阵X=[x1,x2,…,xn]T∈Rn×m,其中X 的每一列代表一个测量变量,每一行代表一个样本.首先对X 进行零均值单位方差的标准化处理,定义标准化后的样本集的协方差矩阵为
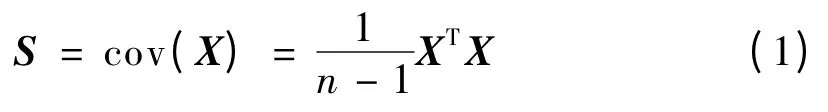
对其进行特征值分解,并且按照特征值的大小顺序排列.PCA 模型对X 进行如下分解:
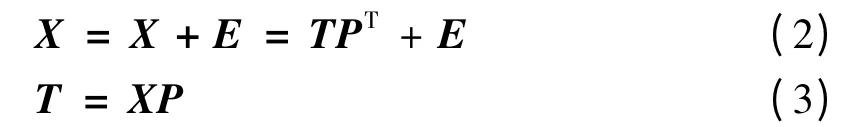
其中,P ∈Rm×A为负载矩阵,由S 的前A 个特征向量构成.T ∈Rn×A为得分矩阵,T 的各列被称为主元变量,A 表示主元的个数,也是得分矩阵的列数.
现使用多向主元分析的方法研究批次过程数据,在忽略次要的非线性关系的同时,假定各个过程参数分别符合高斯分布,可以将PCA 的方法用到批次展开后的数据阵中.
2.2 第一主元贡献率
原始矩阵X ∈Rn×m所对应的协方差矩阵是S ∈Rm×m,协方差矩阵S 对应的特征向量矩阵是Q ∈Rm×m,其中前A 个组成的矩阵就是负载矩阵,根据特征值特征向量公式:SQ=λQ 可以计算出协方差矩阵的m 个特征值:λ1,λ2,…,λm.
累积方差百分比表征的是前k 个特征值的和占总体方差总和的比率.它的计算方法如下:
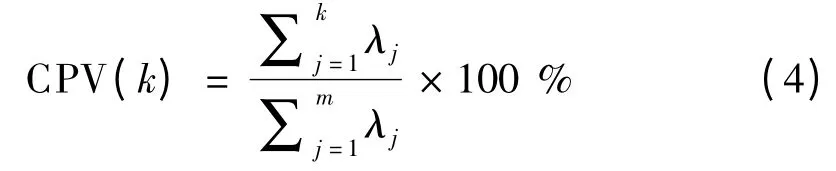
其中,第一主元的累积方差百分比可以表示为:
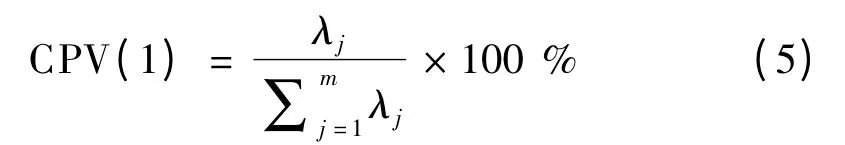
CPV(1)表示第一主元所携带的信息占原始数据总信息的比例,能反映原始数据的主要信息.CPV(1)在主元分析中的作用一方面表现了第一主元提取原始数据信息量的多少,另一方面也可反映数据变量之间的相关性信息和动态关系.如果数据间的动态关系保持不变,那么CPV(1)的值将基本恒定[6].用相邻两个采样时刻对应的数据段的CPV(1)的差值表示2 个数据段所含信息量的差异.当差值最大时,表明数据段的主要信息发生了很大变化,段落由此划分.因此,以CPV(1)差值的变化为指标来确定批次内部不同阶段间动态特性的转变.
2.3 基于第一主元贡献率差值的分段方法
批次过程中的变量并不是全都可以用于分段算法.在批次分段过程中引入某些恒值、多变性的变量,会使分段效果不明显,甚至使过程不能分段.所以,在对批次过程进行分段的过程中,首先要分析原始数据,筛选出适合分段的变量.筛选变量的基本原则是选取变量轨迹具有分段特点的变量,不选取波动不大和波动过于剧烈的变量.进行分段算法的具体流程如图2 所示.
基于第一主元贡献率变化分阶段算法如下:
(1)筛选出合适变量的数据集合(I ×K ×J),在此基础上,得到K-1 个子阶段,每个阶段的数据长度为[t,t+1,…,K](t=1,2,3,…,K-1),其中t 为采样时刻;
(2)对于每个子阶段应用基于变量的展开方式展开为X(I(K-t+1)×J),建立PCA 模型;
(3)每个子阶段,计算CPV (1)1×t={CPV(1)t},当t >2 时,计算每个子阶段与前一子阶段CPV(1)的变化,即d=CPV(1)t-CPV(1)t-1,得到相邻两个子段第一主元累计贡献率差值集合{d(t)};
(4)当{d(t)}达到最大值时,若其所对应的采样时刻t 满足K-t >l 且t-1 >l,其中l 为根据经验确定的边缘效应值,不同生产过程l 的数值一般不同,则第一次分阶段的时刻即为t 时刻,并将整个过程分为2 个阶段[1,2,…,t-1]和[t,t+1,…,K];若不满足上述条件,则不分段.
(5)对分好的各个段重复步骤(2)到(4),直到每个阶段不可以继续分段,结束[7].
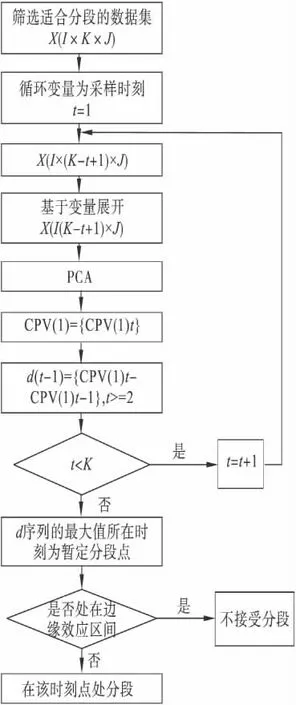
图2 第一主元贡献率差值分段流程Fig.2 Flow chart of phase-dividing using CPV(1)method
3 仿真实验
3.1 青霉素仿真数据的分段实验
青霉素发酵是一个典型的补料分批发酵过程,根据操作主要分为两个部分:第一部分为发酵前期,是间歇式操作.在这个过程中菌体会消耗掉大量的葡萄糖(反应底物),当葡萄糖的溶度过低时反应进行到第二阶段,是半间歇补料操作.为了保持青霉素有较高的产率,细胞生长速率必须保持在某一最小值以上,因此,在这一操作阶段葡萄糖要连续地添加到发酵反应罐中.这一操作过程又包括青霉素合成期和菌体死亡期.从青霉素菌体的生长过程看,该过程可以分为3个阶段.
青霉素仿真软件产生的是一个18 个变量的数据集.仿真实验中,采用文献[5]中选用和处理变量的方法.选择这18 个变量中的第4、8、9、10、14、17 变量进行分段实验.这几个变量的物理含义分别为:底物供给速度、生物总量、青霉素溶量、反应体积、产热量、冷水流量.
用pensim 软件产生50 批次的青霉素数据.为体现间歇过程特点,所得到的50 批次数据是不等长的,即整体反应时间和每个批次内部阶段工时都不等长.在间歇阶段中选取变量10 为指示变量,通过体积的减小来反映发酵过程的进程.通过底物加入速度(变量4)可以计算出底物加入量占总体加入量的百分比,是递增变量,选作半间歇过程指示变量,并假设当14 L 的葡萄糖加入到反应器时整个发酵过程结束.在间歇操作阶段,随着体积每减少1 %,其他的变量通过线性插值的方法进行重新采样;在半间歇操作阶段,葡萄糖每加入总量的0.2 %,其他变量相应地重新进行采样.通过批次轨迹同步化后达到所有批次的采样个数及数据长度相同,这两个阶段的数据长度分别为101 个和501 个,每一批次的数据长度都是602 个.轨迹同步化后的训练集X变为(50 ×602 ×6)的三维矩阵.基于变量展开为二维矩阵(50 ×602)×6.
在该算法中,选取青霉素工艺过程对应的边缘效应为25.在图3(a)中,d 的最大值在第101采样时刻处.在已经分好的2 个阶段内部重新采用分段算法,前101 个采样时刻所对应的第一主元贡献率差值的变化如图3(b)所示,第一主元贡献率差值最大值在边缘效应范围内,不可以再分段.对102-602 采样时刻进行分段,第一主元贡献率的差值如图3(c)所示,在第405 时刻达到最大值,可以对这一部分继续分段.从这一阶段又分出的两部分应用该算法所得到的第一主元贡献率差值如图3(d)和图3(e)所示,均不可以再分段.
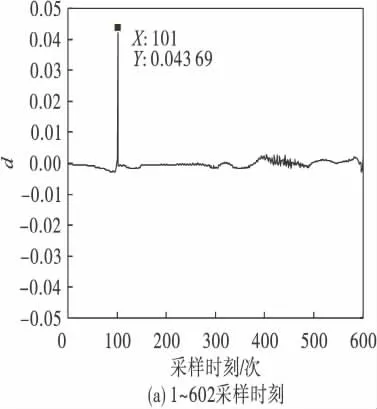
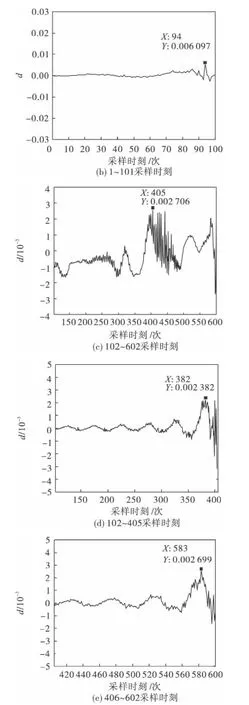
图3 青霉素数据第一主元贡献率差值Fig.3 The differential chart of CPV(1)of pensim data
通过以上操作,青霉素602 个采样时刻被分为3 个阶段:第1 时刻到第101 时刻对应第1 阶段发酵前期;第102 时刻到第405 时刻对应第2阶段青霉素合成期;第406 时刻到602 时刻对应第3 阶段菌体死亡期.分段结果与青霉素菌体生长的实际生物过程一致.
3.2 半导体生产过程分段实验
半导体数据是从铝板蚀刻机的工业生产过程中采集的[9].共采集了107 批的正常批次数据.这些数据记录了3 个不同模态下过程变量变化.该半导体生产过程实际可分为3 个阶段.
图4 给出了第7 和第20 个变量数值波动情况.从这两个变量的波动轨迹可以直观地分辨出数据的分段位置.该过程产生的数据含有21 个变量.选取利于分段的第7、9、12、15、20 变量用于半导体数据的分段.考虑到传感器初始化,不使用前6 个采样时刻数据.从第7 个采样数据开始,采用最短长度法,每个批次保留85 个采样时刻,然后进行分段.首先根据经验选择边缘效应长度为5.不同采样时刻的第一主元贡献率差值结果如图5(a)~(e)所示.
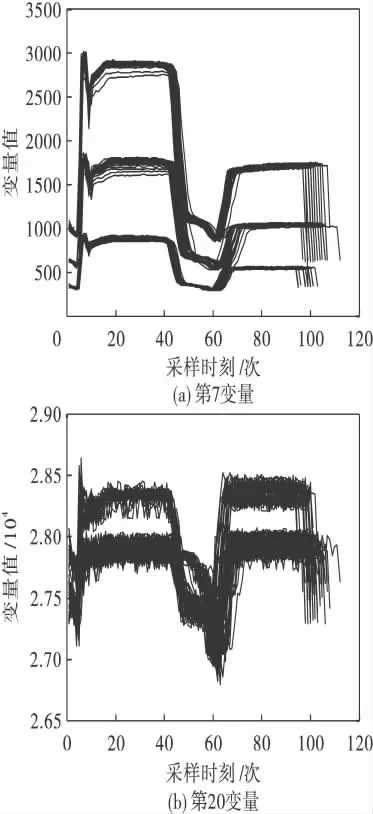
图4 半导体数据变量Fig.4 The variables of the semi-conductor data

图5 半导体数据第一主元贡献率差值Fig.5 The differential chart of CPV(1)of semi-conductor data
由图5 可知:半导体数据可分为3 段:第1时刻到第43 时刻对应第1 阶段,第44 时刻到第61 时刻对应第2 阶段,第62 时刻到第85 时刻对应第3 阶段.考虑到去除前6 个采样时刻,实际的分段时刻为49 采样时刻和70 采样时刻两处,很好地反映出实际的生产阶段.
4 结论
对青霉素批次数据训练集进行主元分析后,用第一主元贡献率差值的方法寻求批次过程分段.实验表明:这种算法能较好地完成批次过程分段,并且与实际的青霉素生长阶段一致.然后将这种算法应用到半导体实际生产数据中,分段效果同样明显,验证了分段理论的有效性.批次过程分段理论能将批次故障范围缩小,对于故障检测具有重要意义.
[1]Nomikos Paul,Macgregor John F.Muti-way Partial Least Squares in Monitoring Batch Processes[J].Chemometries and Intelligent Laboratory Systems,1995,30(1):97-108.
[2]Nomikos Paul,Macgregor John F.Monitoring Batch Processes Using Multi-way Principal Component Analysis[J].AIChE Journal,1994,40(8):1361-1375.
[3]李元.MPCA 在间歇反应过程故障诊断中的应用[J].化工自动化及仪表,2003,30(4):10-12.
[4]赵春晖,王福利,姚远,等.基于时段的间歇过程统计建模、在线监测及质量预报[J].自动化学报,2010,36(3):366-372.
[5]孟艳.多阶段间歇过程监测中动态特性转变的识别方法的研究[D].北京:北京化工大学,2009:15-18.
[6]张佳.基于多阶段MPCA 方法的间歇过程监测研究[D].北京:北京化工大学,2009:43-48.
[7]Sun Wei,Meng Yan,Palazoglu Ahmet,et al.A Method for Multiphase Batch Process Monitoring Based on Auto Phase Identification[J].Journal of Process Control,2011,21(4):627-638.
[8]周东华,李钢,李元.数据驱动的工业过程故障诊断技术[M].北京:科学出版社,2011:23-29.
[9]Wise B M,Gallagher N B,Butler S W,et al.A Comparison of Principal Component Analysis,Multiway Prin-cipal Component Analysis,Trilinear Decomposition and Parallel Factor Analysis for Fault Detection in a Semiconductor Etch Process[J].Chemo-motrics,1999,13:379-396.

