基于改进K-means 聚类的kNN 故障检测研究
陈海彬,郭金玉,谢彦红
(沈阳化工大学 信息工程学院,辽宁 沈阳 110142)
现代化工工业具有大规模、高危性、多变量的特点,随着设备结构日趋复杂,其故障类别日益增多,反映故障状态、特征的变量也相应增加.在实际检测过程中,为了使检测准确可靠,总要采集尽可能多的数据样本,以获得足够多的信息.
当前,对工业过程故障检测的研究方法有3类[1-2]:基于数学模型的方法、基于人工智能的方法和基于数据驱动的方法.基于数据驱动的方法正成为故障检测领域内的研究热点.常用的是统计过程控制(Statistics Process Contol,SPC)方法.统计过程控制(SPC)的基本概念是通过判断当前数据是否在正常数据附近来检测故障,这种判断是基于当前数据所在正常数据的概率密度基础上的.通常估计多维空间的概率密度很困难.为了避免估计多维概率密度函数及处理过程的非线性和时变性,Peter He Q 提出了基于k 近邻规则(k-Nearest Neighbor Rule,kNN)的故障检测算法[3-4],这种方法简单、直观,不足之处是计算量较大,因为对每一个待分类的样本都要计算它到全体已知样本的距离,才能求得它的k 个最近邻点.
一条生产线在生产过程中往往会出现几种不同工况,而对于采集到的数据样本的分类边界常常是不确定的.这种多工况的生产过程阻碍了kNN 故障检测方法的在线应用.因为在数据工况不明了的情况下,不加区分地对其进行kNN 故障检测很容易产生误报或者漏检情况.为了减少计算量,提高故障检测准确性,本文研究基于改进K-means 理论的kNN 故障检测方法.首先利用改进K-means 方法对仿真生成的青霉素数据进行聚类,然后利用kNN 方法进行故障检测,并与未进行分类而直接进行kNN 故障检测的方法进行了比较.
1 基本方法研究
1.1 改进K-means 基本理论
J.B.MaeQueen 在1967 年提出的K-means 算法是一种应用非常广泛的聚类算法.K-means 算法属于聚类方法中一种典型的划分方法,它是一种首先给出聚类类别数的聚类算法.1999 年Jian等对K-means 算法进行了改进,其基本操作是子类合并,通过定义两个子类中心的最小距离的阈值θ,来获得最优的子类数量和子类中心.该算法实际上通过定义一个合适的θ,折中考虑了模型的准确性和复杂性[5].
算法的输入是待分类样本{x1,x2,…,xn},以及两个子类中心的最小距离阈值θ.算法的输出是子类数量C,子类中心{W1,W2…Wc}.
聚类算法的具体步骤为:
(1)在空间内放置k 个数据点,这些数据点代表初始聚类的中心,一般是从样本中均匀抽取的.
(2)若两个子类中心的距离小于预定的阈值θ,剔除其中一个聚类中心.
(3)将每个对象分配到离它最近的中心聚类.
(4)Inum次迭代后,若某子类中心没有俘获一定数量的样本,则剔除该类.
(5)当所有对象都分配之后,重新计算出k个中心点的位置.
(6)如果算法满足收敛条件则结束,否则返回步骤2.
(收敛条件有:两次迭代中的聚类中心距离的变化小于一个很小的数ε,或者每个子类中样本到子类中心的距离平方和以及子类之间的距离平方和达到最小)
改进K-means 算法是目前用于科学研究的聚类算法中极具影响的一种技术,它能够很好地根据数据的特性将数据收敛为K 类.对于多工况数据,由于不同工况的工作条件不同,采集到的数据特性也会有所不同,从而利用改进Kmeans 算法可以很好地将不同工况的数据分别聚为一类.同时,从以上过程可以看出:改进Kmeans 算法的主要优点在于算法简单、快速,且能有效处理大规模数据,能够很好地弥补kNN计算量大的缺点.
1.2 基于kNN 的故障检测
基于kNN 的故障检测算法的思想是正常样本的轨迹与训练样本的轨迹相似,而故障样本的轨迹偏离训练样本的轨迹,故障样本与最近邻训练样本的距离大于正常样本相应的距离.通过确定训练样本与最近邻的训练样本距离的分布,就可以定义具有一定置信水平的阈值.如果未分类的样本与最近邻训练样本的距离小于阈值,则这个样本是正常的;否则样本是故障的[3-4].基于kNN 的故障检测方法由两部分构成:建立模型和故障检测.
(1)建立模型
①在训练数据集合中找到每个样本的k 个最近邻.
②对每个样本计算k 个最近邻距离的平方和.第i 个样本的k 个最近邻距离的平方和定义为:

③确定进行故障检测的阈值.由于D2i 的分布逼近非中心的χ2分布,可以确定具有置信水平α 的阈值确定阈值的另外一种常用方法是在正常操作条件下基于训练数据.
(2)故障检测
对未分类的样本X,故障检测部分由3 步组成:
①从训练集合中找到样本X 的k 个近邻.
1.3 基于改进K-means 的kNN 故障检测
一条生产线在生产过程中往往会出现几种不同工况,而对于采集到的数据样本的分类边界常常是不确定的,因此,需要对采集到的原始数据进行聚类.下面运用改进K-means 方法进行聚类,然后利用kNN 方法进行故障检测,从而使故障诊断能够更加精确.基于改进K-means 的kNN 方法综合了两种方法的优点,由建立模型和故障检测两步组成.具体步骤为:
(1)建立模型
①通过改进K-means 将原始建模数据分为C 个类,每一类的中心为Wc(c=1,2,…,C);
②利用kNN 方法,计算每类k 个邻近距离平方和的阈值.建立模型过程如图1 所示.

图1 基于改进K-means 的kNN 建模流程Fig.1 kNN modeling flow chart based on improved K-means
(2)故障检测
①对新的待检测样本,分别与每类的中心Wc求距离,将该样本分配到离它最近的中心聚类;
②在该待检测样本所在的聚类中,通过kNN 方法进行故障检测,判断其是正常还是故障.具体过程如图2 所示.
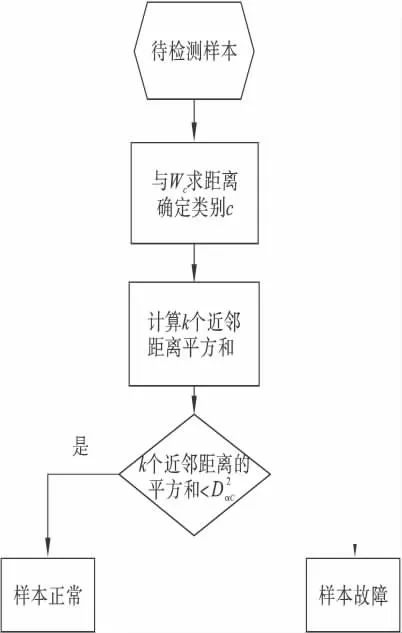
图2 基于改进K-means 的kNN 故障检测流程Fig.2 kNN fault detection flow chart based on improved K-means method
2 仿真研究
2.1 青霉素数据
青霉素作为一种抗生素,具有广泛的临床医用价值,其生产过程是一个典型的非线性、动态、多阶段间歇生产过程[6].文中运用的数据来自美国Illinois 州立理工学院AliCinar 领导的过程监控与技术小组设计的青霉素生产仿真软件Pensim 2.0.通过该软件可以仿真不同初始条件下的青霉素生产过程的各个变量.影响青霉素发酵过程的可在线测量变量主要有空气流量、搅拌功率、底物流加速度、温度、反应体积等[7].
选取3 种工况75 个正常批次,其中每批次18 个变量,采样样本400(每1 h 采样1 次).3 种工况反应体积分别设为130、160 和190 L,每种工况各产生25 个批次.为验证该方法对多工况故障诊断的效果,对应3 种工况,在200 h 对通风率和搅拌功率分别加入5 %、10 %的斜坡误差,直到结束,每种工况各产生4 批故障数据.
2.2 数据预处理
间歇过程数据是三维矩阵,在进行故障检测前需要对数据进行预处理.将每一批次的二维数据按时间展开成一维数据,如图3 所示.
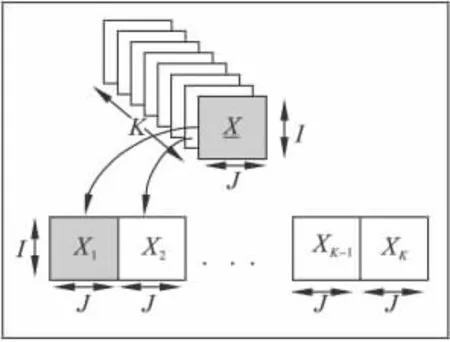
图3 数据展开方法Fig.3 Data unfold method
图3 中I 表示采样批次,J 表示变量,K 表示采样时刻.对于每一批次,将每一个采样时刻所有变量的数据横向展开可得到一个1 ×(400 ×18)的矩阵,所有建模数据展开后得到一个75 ×(400 ×18)的二维矩阵,所有故障数据展开后得到一个12 ×(400 ×18)的二维矩阵.
2.3 改进K-means 对青霉素数据聚类
图4 为通过改进K-means 对75 批次的正常数据进行聚类的结果.其中75 批次数据分成了3 类,表明75 批次数据是在3 种不同工况下产生的,这与数据采集仿真时的设定一致.
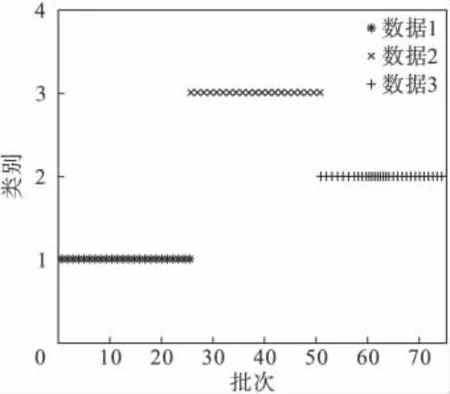
图4 基于改进K-means 方法的青霉素数据聚类Fig.4 The penicillin data clustering based on improved K-means method
为了验证模型的有效性,现从3 种工况中各随机抽取2 个批次作为校验批次,加入故障数据,从而得到新的建模数据为69 ×(400 ×18),新的待检测数据为(12 +6)×(400 ×18).
2.4 仿真结果与分析
在传统kNN 故障检测方法中k 的取值为3,如图5 所示前12 个批次为故障批次,后6 个批次为校验批次.图中虚线对应95 %的控制限.从图5 中可以看出:传统kNN 故障检测方法可以检测到所有的12 个故障批次,但是对第1 个工况的1 个校验批次产生了误报情况.对于产生这种结果有两种原因:(1)控制限设置为95 %,允许5 %的误差出现,造成了1 个校验批次的误报;(2)3 种不同工况的数据统一处理,将会把整体数据的控制限向下拉低,使平均距离较大工况的数据更容易超出控制限,产生误报.
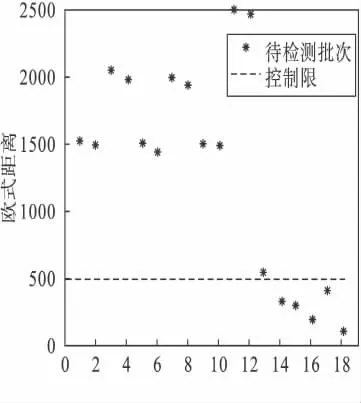
图5 传统kNN 的故障检测Fig.5 The traditional kNN fault detection
基于改进k-means 的kNN 故障检测算法首先对3 种工况进行建模,对待检测的批次进行工况归属判断,然后通过对应工况的kNN 故障检测模型进行检测,其中k 取值为3.检测结果如图6 所示.图中虚线对应95 %的控制限.
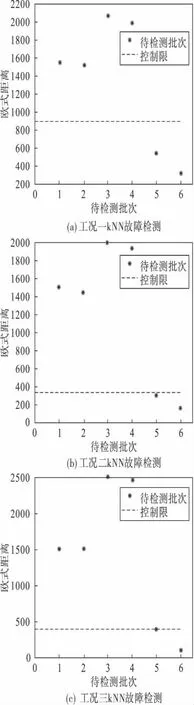
图6 基于改进K-means 的kNN 故障检测Fig.6 kNN fault detection based on improved K-means method
从图6 可以看出:基于改进K-means 的kNN 故障检测不但完全检测出了所有的12 个故障批次,而且对6 个校验批次没有产生误报,提高了准确性.同时,可以确定在传统kNN 的故障检测中,第1 工况产生的1 个校验批次误报情况,不是由正常的5 %误差引起的,而是由数据分类不精确造成.
由于各工况的χ2分布不同会引起各工况控制限的不同,通过先分类再进行故障检测的方法,可以精确地计算出每种工况的95 %控制限,而不是将所有样本混为一谈.同时,通过先分类再建模,对校验批次进行kNN 故障检测时,待测批次不需要与全部的69 个建模批次求欧式距离,只需要先与3 个聚类中心求距离,判断该待测批次的工况归属后,再与所在工况的23 个建模批次求欧式距离,大大缩减了故障检测时间.
通过对比可以看出:基于改进K-means 的kNN 故障检测算法对于多工况特性的生产过程故障检测可以取得较好的效果.但对于单一工况生产过程,采集到的数据特性全都相似,利用改进K-means 聚类最终会收敛为一类,此时改进K-means 的kNN 故障检测方法与传统的kNN故障检测方法检测效果一致,但计算量却增大,有待进一步改进.
3 结论
间歇生产过程复杂的非线性和多工况特性,使传统的kNN 单一模型进行故障检测的难度加大.基于改进K-means 聚类kNN 故障检测方法对间歇过程分工况建模,能够更好地描述各工况的机理特性,大大提高了故障检测的准确性.将该方法应用于青霉素批次过程的故障检测中,通过和传统的kNN 故障检测结果相比较,表明改进K-means 聚类kNN 故障检测方法提高了故障检测的准确性和实时性.在实际生产中有重要的指导意义.
[1]刘强,柴天佑,秦泗钊,等.基于数据和知识的工业过程监视及故障诊断综述[J].控制与决策,2010,25(6):801-807.
[2]万福才,鄂佳.统计过程监控综述[J].沈阳大学学报,2009,21(3):101-103.
[3]He P Q,Wang Jin.Principal component based knearest-neighbor rule for semiconductor process fault detection[C]//American Control Conference,June 11-13,2008.Seattle:conference Publications,2008:1606-1611.
[4]He P Q,Wang Jin.Fault Detection Using the k-nearest Neighbor Rule for Semiconductor Manufacturing Processes[J].IEEE Transactions on Semiconductor Manufacturing,2007,20(4):345-354.
[5]曹文平.一种有效k-均值聚类中心的选取方法[J].计算机与现代化,2008,15(3):95-97.
[6]刘世成,王海青,李平.青霉素生产过程的在线统计检测与产品的质量控制[J].计算机与应用化学,2006,23(3):227-232.
[7]Birol G,Cinar A.A Modular Simulation Package for Fed-batch Fermentation:Penicillin Production[J].Computers &Chemical Engineering,2002,26(11):1553-1565.

