改进的Simpson公式及其代数精度

杨少华，华志强

（1.辽宁大学 经济学院，辽宁 沈阳 110036；2.阜阳师范学院 数学与计算科学学院，安徽 阜阳 236037；3.内蒙古民族大学 数学学院，内蒙古 通辽 028043）

在解决实际问题的过程中，经常会遇到一些被积函数的原函数不易求得或根本就不存在的情况，因此，用数值方法求问题的近似解就成为解决问题的重要途径.为了提高近似解的精度，要对数值求积公式进行校正以期得到误差较小的近似解.本文利用Simpson 数值求积公式余项“中间点”的渐近性对其进行校正，从而得到代数精度较高的数值求积公式.

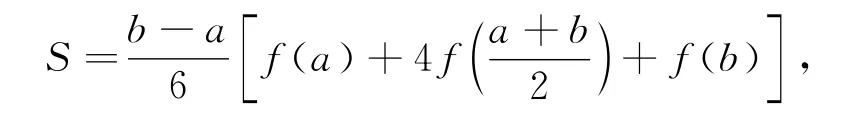
其插值余项

1 渐近性定理

定理1 设函数f（t）在区间［a，x］上连续，在a的某邻域内直到n＋5次可导，且f（n＋5）（a）≠0，则对于由

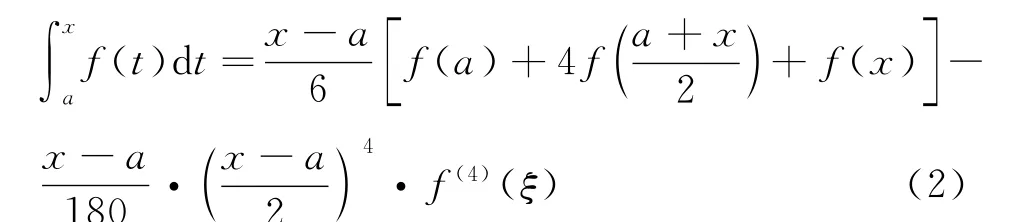
确定的ξ（ξ∈（a，x）），有下式成立：

证明 令

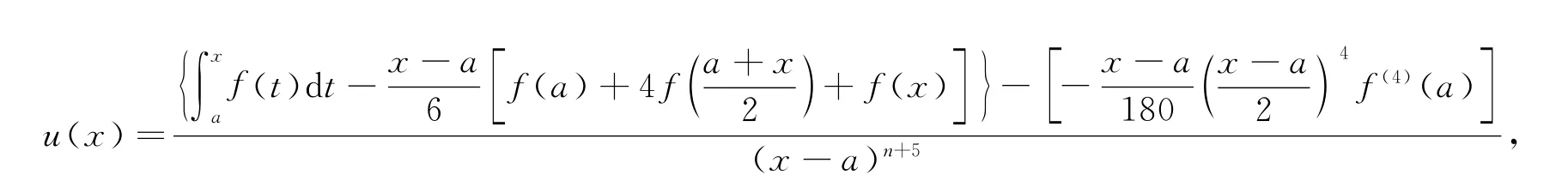
反复应用洛必达法则，得

由式（2）并反复应用洛比达法则，得

比较式（3）与式（4），有

所以

因此

特别地，当n＝1时，可以得到以下推论.

推论 设函数f（t）在区间［a，x］上连续，在a的某邻域内直到6次可导，且f（6）（a）≠0，则对于由式（2）确定的ξ，有下式成立：

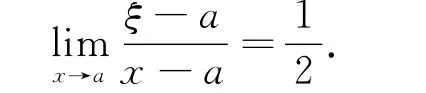
证明 当n＝1时，利用定理1的结论，可得：

2 校正后的Simpson数值求积公式及其代数精度

定理2 设函数f（t）在区间［a，x］上连续，在a的某邻域内直到5次可导，且f（5）（a）≠0，则定积分f（x）dx 有如下数值积分公式：

定理3 设函数f（t）在区间［a，x］上连续，在a的某邻域内直到5次可导，且f（5）（a）≠0，则校正后的Simpson数值求积公式（5）具有5次代数精度.

证明 不失一般性，考查a＝0的情形.

当f（t）＝ti（i＝0，1，2，3）时，式（4）左边等于右边，下面考查f（t）＝t4，t5时，式（5）左右两边是否相等.把f（t）＝t4，a＝0，x＝1代入

把f（t）＝t4代入式（5）左右两边，得

所以，当将f（t）＝t4代入式（5）时，左边与右边相等.

把f（t）＝t5＋（1-t）5，a＝0，x＝1 代入式（6），有

把f（t）＝t5代入式（5），得

所以，当将f（t）＝t5代入式（5）时，左边与右边也相等.但将f（t）＝t6代入式（5），左右两边不等，根据数值求积公式代数精度的定义知式（5）的代数精度为5.

综上，校正后的Simpson数值求积公式S′的代数精度为5，而Simpson数值求积公式S的代数精度只有3［6-7］，因此，校正后代数精度提高了2阶.

3 结 语

在用数值方法求积分值时，随着积分区间添加节点数的增加，往往会造成数值求积公式不稳定.因此，为了提高精度，通常把积分区间等分成若干子区间，在每个子区间上使用低阶求积公式，这就是复合求积法.上面已经得到代数精度较高、低阶的改进Simpson数值求积公式，下面利用建立复合Simpson数值求积公式的思想，给出改进的复合Simpson数值求积公式.

将区间［a，b］分为n 等份，在每个子区间［xk，xk＋1］上采用改进的Simpson 数值求积公式，则称

为改进的复合Simpson数值求积公式.其中，xk

在用数值方法求积分近似值的过程中，应该使用改进的复合Simpson数值求积公式，因为它会带来更为准确的计算结果.

［1］郑华盛，胡结梅，李羲.一种确定求积公式余项的新方法［J］.南昌航空工业学院学报：自然科学版，2002，16（3）：4-7.（Zheng Huasheng，Hu Jiemei，Li Xi.A New Method for Solving Remainder Term of Integral Formulae［J］.Journal of Nanchang Institute of Aeronautical Technology：Natural Science，2002，16（3）：4-7.）

［2］Jacobson B.On the Mean Value Theorem for Integrals［J］.Amer.Math.Monthly，1982（89）：300-301.

［3］Zhang Baolin.A Note on the Mean Value Theorem for Integrals［J］.Amer.Math.Monthly，1997（104）：561-562.

［4］刘彬清.关于一些数值求积公式的渐进性［J］.应用数学与计算数学学报，2000，14（2）：83-87.（Liu Binqing.On Asymptotic Analysis for Some Numerical Integral Formulas ［J］.Communication on Applied Mathematics and Computation，2000，14（2）：83-87.）

［5］杨少华，华志强.Cotes 数值求积公式的校正［J］.数学杂志，2012，32（4）：644-648.（Yang Shaohua，Hua Zhiqiang.The Correction of Cotes Numerical Integration Formula ［J］.Journal of Mathematics，2012，32（4）：644-648.）

［6］牛彦.数值积分式中代数精度的讨论［J］.沈阳大学学报，1998，10（4）：109-111.（Niu Yan.Discussion about Algebraic Precision in Numerical Value ［J］.Journal of Shenyang University，1998，10（4）：109-111.）

［7］李庆扬，王能超，易大义.数值分析［M］.4版.武汉：华中科技大学出版社，2006.（Li Qingyang，Wang Nengchao，Yi Dayi.Mathematics Numerical Analysis［M］.4th ed.Wuhan：Huazhong University of Science ＆ Technology Press Co.，Ltd，2006.）