CFRP布加固钢筋混凝土梁黏结应力分析

周 乐，聂红宾

（沈阳大学a.建筑工程学院，b.辽宁省环境岩土工程重点实验室，辽宁 沈阳 110044）

CFRP布加固技术具有提高混凝土的部分承载力，改善混凝土的延性，提高抗震性能，减小混凝土的截面等优点［1］，CFRP布加固钢筋混凝土结构技术已经在实际工程中广泛应用.为了进一步提高CFRP 布的加固效率，CFRP 布黏结问题越来越引起人们的关注.杨树桐［2］对FRP加固钢筋混凝土三点弯曲梁进行断裂研究，利用Lagrange乘数法得到载荷和等效裂缝长度模型，对FRP裂缝进行了深入研究.李贵炳［3］通过实验指出，用CFRP纤维片材锚固方式容易使片材撕裂.李松辉等［4］阐述了CFRP 布加固梁各受力阶段的剥离机理，指出了粘贴基面混凝土剥离的主要原因.本文通过外力法求出结构胶体表面黏结力，通过胶体的内力分析，得出破坏类型以及裂缝的发展趋势.

1 基本假定

为了更好地分析CFRP 布加固钢筋混凝土梁的黏结性能，作如下几点假定：①CFRP布在破坏过程中始终处于线弹性范围内；②CFRP 布的脱落、拉断只发生在梁的受弯区；③CFRP布厚度很薄，厚度可以忽略不计，认为沿纤维方向各向同性、应力分布均匀；④混凝土、CFRP 布和胶体作为一个整体符合平截面假定；⑤在线弹性阶段，混凝土、钢筋、结构胶体和CFRP布协同工作.

2 内力的计算

为了对黏结应力进行系统的研究，采用计算简图，如图1a 所示；对作用在梁上的任意载荷q（x）进行简化，如图1b所示；内力分析，如图1c所示.下面计算梁内任一点的内力.

由力平衡原则，对A 点取矩，有

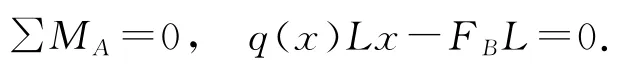
式中，q（x）为任意载荷；L为梁的长度；x为合力点到A 支座反力的距离；FB为梁的支座反力.由上式可得FB＝q（x）x.

对B 点取矩，有

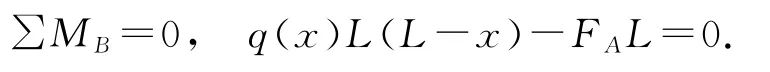
式中，FA为梁的支座反力.由上式可得FA＝q（x）×（L-x）.

对于梁内任一点的轴力FN，因为没有考虑水平载荷，只有竖向载荷，所以

由于∑Fy＝0，所以

对杆件右端取矩，有

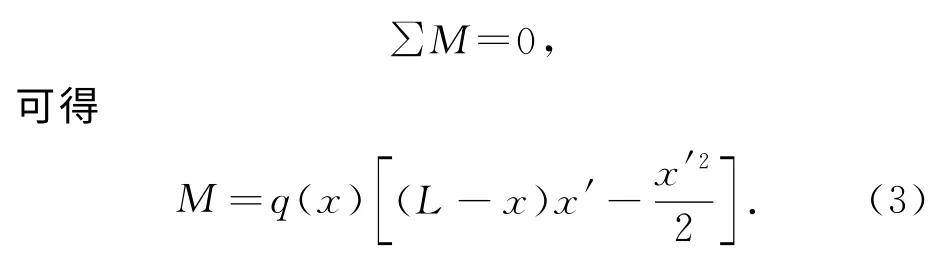
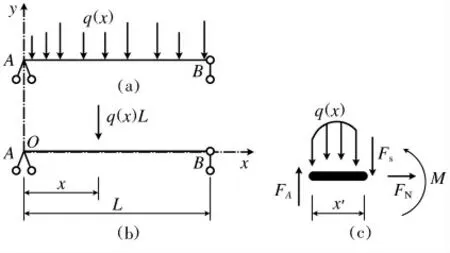
图1 结构内力计算简图Fig.1 Calculation diagram of internal force

3 黏结应力的计算和黏结破坏

3.1 黏结应力

加载初期，CFRP 布、结构胶体和混凝土的受力均很小，并且都处于线弹性阶段，能很好地进行协同工作.根据文献［5］，取长为dt的CFRP布加固混凝土段为研究对象.设宽度为l，有任意竖向载荷作用在研究对象上.如图2所示.

以混凝土为研究对象.混凝土的高度为h，有效高度为h0，钢筋的轴心到混凝土保护层的距离为as，研究对象截取的长度为dt，厚度为l.

基于极限平衡理论，y 轴方向合力为零，即∑Fy＝0，所以

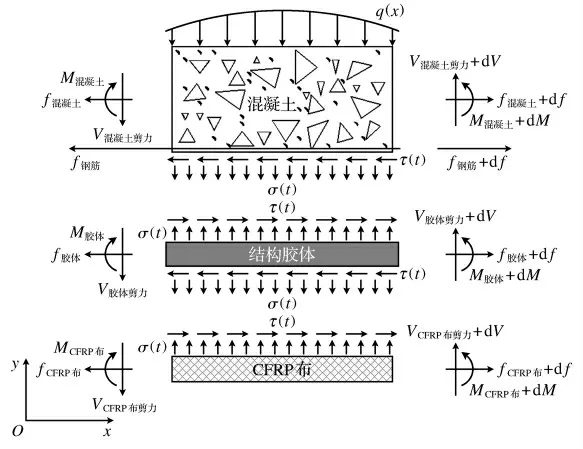
图2 梁线弹性阶段内力图Fig.2 The internal force diagram of beam linear elastic stage

式中，σ（t）为表面拉应力；V混凝土剪力为混凝土剪力.

x 轴方向合力为零，即∑Fx＝0，所以

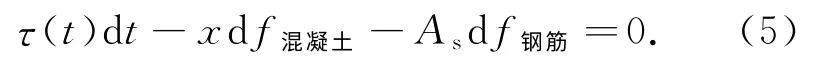
式中，τ（t）为表面切应力；x为受压区高度；f混凝土为混凝土抗拉强度；f钢筋为钢筋的抗拉强度；As为钢筋的截面面积.

对钢筋左端取矩，得∑M＝0，所以

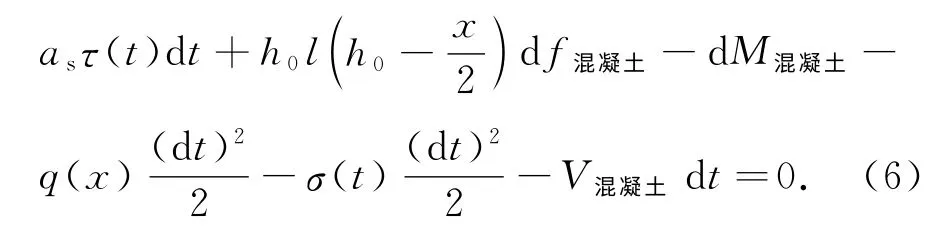
式中，as为混凝土的保护层；h0为混凝土的有效高度；M混凝土为混凝土的弯矩.

以胶体为研究对象.假设在线弹性阶段，胶体的中性轴未发生移动；胶体的厚度取l，长度为dt.

对于x 轴合力为零，即∑Fx＝0，所以

式中，f胶体为结构胶体的抗拉强度.说明胶体拉力不发生变化.

对于y 轴合力为零，即∑Fy＝0，所以

式中，V胶体剪力为结构胶体所受的剪力.说明胶体剪力不发生变化.

对胶体左端取弯矩，得∑M＝0，所以

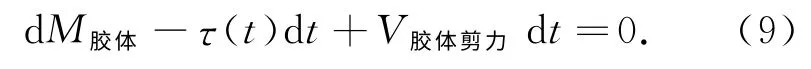
式中，M胶体为结构胶体所受的弯矩.

以CFRP 布为研究对象.对于x 轴合力为零，即∑Fx＝0，所以

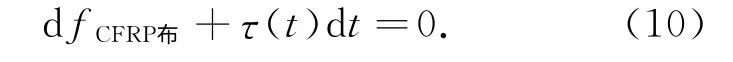
式中，fCFRP布为CFRP布的抗拉强度.

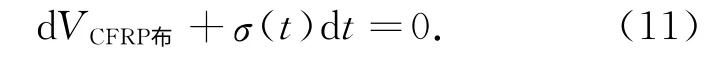
对于y 轴合力为零，即∑Fy＝0，所以式中，VCFRP布为CFRP布所受的剪力.

对于CFRP布左端中性轴取矩，得∑M＝0，所以

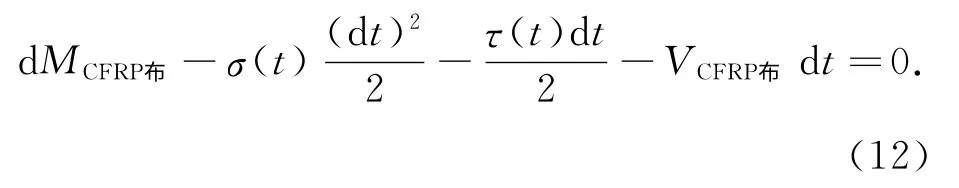
式中，MCFRP布为CFRP布所受的弯矩.

基于方程（1）～（3），得

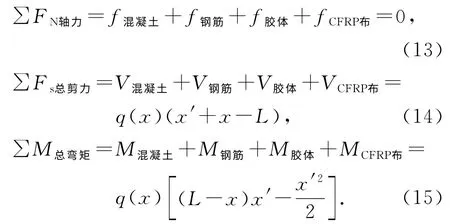
联立方程（4）～（15），得

式中，C1为常数，一般取值为0.

式中，C2为常数，一般取值为0.

由式（14）和式（15），可得σ（t），τ（t）：

由上述式子可知，σ（t），τ（t）可用外载荷q（x）表示，即推导出来的σ（t）、τ（t）与胶体自身的弹性模量E 和剪切模量G 等因素无关.

3.2 黏结破坏

对于胶体的内力，通过对胶体进行单独研究，求出内力.根据文献［6］进行内力简化，如图3所示，再分别求出各个载荷在一点所产生的应力，叠加起来，即可求出胶体内任意一点的应力.

图3 内力简化图Fig.3 Simplified diagram of internal forces

假设τ（t）对胶体只产生弯矩，不考虑因τ（t）所产生的胶体分层影响；σ（t）对胶体只产生竖向拉力作用，不考虑因胶体表面不平而产生的水平剪力.

根据文献［7］，有如下公式：

式中，σ为正应力；M为结构弯矩；y为任意一点到中性轴的距离；IZ为截面惯性矩.

首先，求胶体表面剪应力τ（t）对其产生的应力，根据式（16）可得

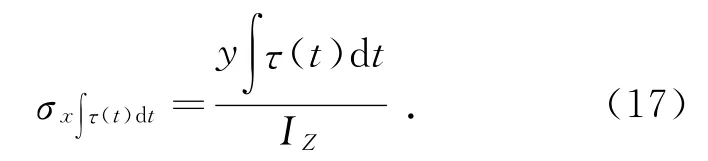
式中，σx∫τ（t）dt为胶体表面剪切力τ（t）形成的弯矩所产生的正应力；y为胶体的1／2厚度；IZ为胶体的截面惯性矩.基于式（16）可得

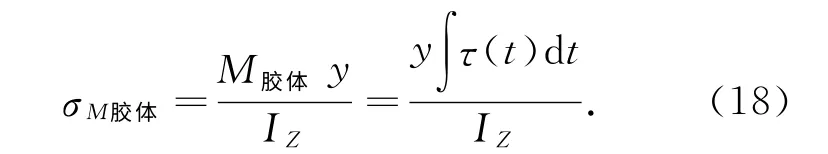
式中，M胶体为胶体的弯矩；y为任一点到中性轴的距离.

其次，求出竖向的拉应力：

式中，∫σ（t）dt为胶体表面拉应力.

由于M胶体产生的应力大小在胶体任意截面都相等，但是τ（t）所产生的弯矩最左边最大，最右边为0，因此，取左端剖面1-1为研究对象，基于式（17）～式（19）得到剖面1-1的应力图，如图4所示.

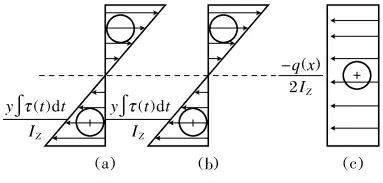
图4 内力计算及应力图Fig.4 Internal force calculation and stress diagram

由图4分析可知，竖向正应力σy始终为正值，胶体竖向受拉.但是对于水平正应力σx，在胶体中性轴以上，胶体水平应力为负值，即胶体受压；中性轴以下，应力为正值，即胶体受拉.对其进行应力组合，当上面受拉时，侧面也受拉，应力状态如图5a所示，最大应力σ1和σ2均为正值；当上面受拉时，侧面受压应力状态如图5b所示.

根据文献［8］，库仑的应力破坏线公式为

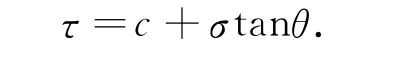
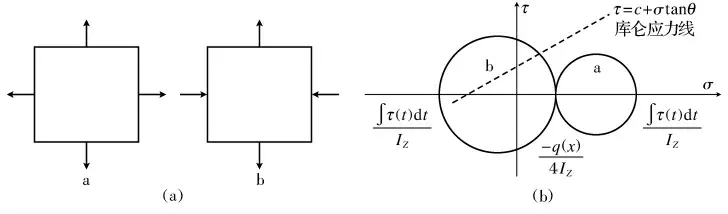
图5 应力组合及莫尔应力圆Fig.5 Combined stress and Mohr stress circle

由图5可知，当胶体处于a状态时，竖向、水平同时受拉，库仑应力破坏线在应力圆a外面.因此，在这种情况下，胶体不会发生破坏；当胶体处于b 状态时，上面应力为正，侧面应力为负值，应力圆如应力圆b 所示，库仑应力破坏线经过应力圆，因此，b应力状态会发生破坏.

根据上述分析，得出如下应力破坏条件：

莫尔应力圆半径

当半径R 满足上述条件时，胶体未达到破坏，反之则发生破坏.

随着载荷的增加，裂缝从黏结剂的上表面发展到下表面，裂缝贯通后，能观察到在裂缝有角度为θ的倾向.

4 结 语

（1）运用极限平衡理论及微积分原理推导出了混凝土、钢筋、胶体和CFRP 布的内力表达式，并求出表面黏结力的公式，此公式适用于结构胶体的任何状态.

（2）表面黏结力的大小与外载荷q（x）的大小、载荷的加载方式、支座类型和跨度有关，与胶体的抗弯刚度、抗剪模量等力学性能参数无关.

（3）胶体裂缝从混凝土与胶体的黏结面处发生，并顺着黏结剂从上往下发展.

［1］赵彤，谢剑.碳纤维布补强加固混凝土结构新技术［M］.天津：天津大学出版社，2001：1-5.（Zhao Tong，Xie Jian.New Technique of Repairing ＆Strengthening Reinforced Concrete Structures with Continuous Carbon Fiber Sheet［M］.Tianjin：Tian Jin University Press，2001：1-5.）

［2］杨树桐.基于断裂力学的钢筋、FRP 与混凝土界面力学特性研究［D］.大连：大连理工大学，2008：244-263.（Yang Shutong.Study on Mechanical Behaviors at Tendon-Concrete and FRP-Concrete Interfaces Based on Fracture Mechanics［D］.Dalian：Dalin University of Technology，2008：244-263.）

［3］李贵炳.碳纤维片材加固钢筋混凝土梁抗弯性能与剥离破坏研究［D］.杭州：浙江大学，2006：110-146.（Li Guibing.Study on Flexural Behavior and Debonding Failure of CFRP-strengthened RC Beams［D］.Hangzhou：Zhejiang University，2006：110-146.）

［4］李松辉，赵国藩，王松根.CFRP加固钢筋混凝土梁各受力阶段的剥离机理［J］.工程力学，2005，22（1）：153-158.（Li Songhui，Zhao Guofan，Wang Songgen.Mechanism of Cover Delamination or FRP Debonding of CFRP Strengthened RC Beams at Different Stage［J］.Engineering Mechanics，2005，22（1）：153-158.）

［5］张鹏.CFRP加固RC梁板受弯性能研究［D］.上海：同济大学，2004：11-13.（Zhang Peng.The Flexural Performance Study on CFRP Strengthening RC Beam and Plate［D］.Shanghai：Tongji University，2004：11-13.）

［6］李廉锟.结构力学：上册［M］.4 版.北京：高等教育出版社，2004：50－60.（Li Liankun.Structural Mechanics：The 1st Volumn［M］.4th ed.Beijing：Higher Education Press，2004：50－60.）

［7］过镇海，时旭东.钢筋混凝土原理与分析［M］.北京：清华大学出版社，2003：205.（Guo Zhenhai，Shi Xudong.Reinforced Concrete Principle and Analysis［M］.Beijing：Tsinghua University Press，2003：205.）

［8］陈希哲.土力学与基础工程［M］.北京：清华大学出版社，2004：100－110.（Chen Xizhe.Soil Mechanics and Foundation Engineering［M］.Beijing：Tsinghua University Press，2004：100－110.）