基于极大代数的阻塞流水车间启发式动态规划调度算法

李彦平，王 帅，赵 月

（沈阳大学 科学技术研究中心，辽宁 沈阳 110044）

流水车间调度问题在生产系统中被广泛应用.它是一类典型的NP难组合优化问题，随着生产任务的增加以及作业任务抵达时间的差异，都将会提高此类问题的求解难度［1］.由于此类问题存在普遍性及复杂性，所以研究流水车间调度问题具有非常重要的的理论意义和实用价值［2］.

流水车间调度问题可以理解为机器之间存在无限个缓冲区，但是在实际的生产中，由于工艺要求不同及作业空间设计受限制等，导致机器间存在的缓冲区往往是有限个，甚至是不存在的［3］.若机器间无缓冲区，当任务n 在第k 个机器上完成加工时，且第k＋1个机器存在作业任务，此时任务n 将会被阻塞在第k 个机器上，直至第k＋1个机器可用，这类问题被称为阻塞流水车间调度问题.

本文详细研究了具有阻塞约束的流水车间调度问题，该问题的目标函数为求解最小化完工时间之和.根据相关文献可知，目前广泛采用启发式算法对此类问题进行求解：文献［4］提出了一种基于折衷策略对工件进行初始排序的启发式算法，并与NEH 算法进行了比较，实验证明其提出的算法要优于NEH 算法；文献［5］设计了一种构造启发式算法，从减少下游工件的滞留时间入手产生工件的初始排序，结合有向图中对关键路径的分析，采用插入规则进行搜索得到工件序列的近优排序.通过与NEH 算法的比较，证明了所提算法的有效性；文献［6］对PF、NEH 算法进行改进和组合，并结合插入邻域搜索算法，提出了PFNEHLS、wFP-NEHLS、PW-NEHLS三种组合的启发式方法，并利用这些方法解决阻塞流水车间调度问题，在Taillard的大规模问题上得到了较优的解.

启发式算法通用性强，容易实现，但是利用启发式动态规划算法求解阻塞流水车间调度问题的研究相对较少.本文基于极大代数思想，针对阻塞流水车间特点建立了数学调度模型，同时采用启发式动态规划算法进行求解.文章针对具体生产加工实例进行求解，通过与表3结果进行比较可知，本文所提出的启发式动态规划调度算法具有可行性.

1 阻塞流水车间调度模型

设：D＝（R＋∪ε，⊗，⊕）为极大代数，⊗为求和运算，⊕为取大运算；阻塞流水车间调度模型可表述为

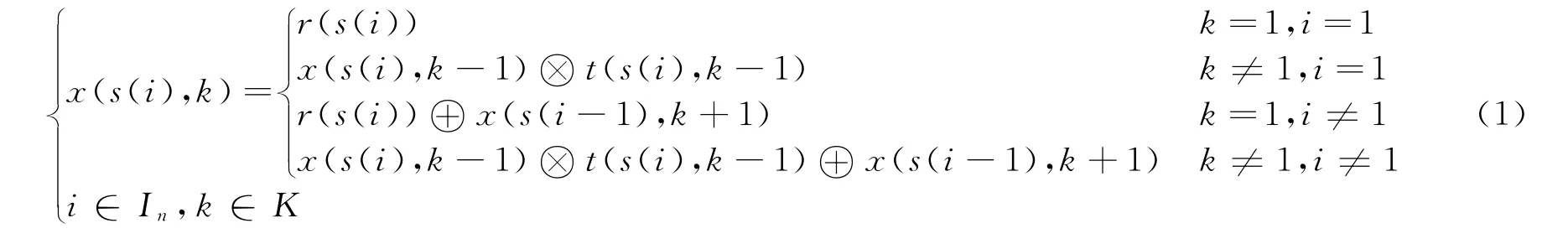
式中：JN＝｛1，2，…，N｝为任务集，N为任务个数；In＝｛1，2，3，…，n｝为排序集，n≤N，n为被排序的任务个数；K＝｛1，2，…，m｝为机器集，m为机器数；t：JN×K ↦D为任务加工时间函数；t（j，k）表示任务j∈J 在机器k 上所需的加工时间；r：JN↦D为任务到达时间函数；r（j）表示任务j∈J的到达时间或者称为准备就绪最早时间；x：JN×K ↦D为任务开始加工时间函数；x（j，k）表示任务j∈J 在机器k 上的最早开工时间；c：JN×K ↦D为任务完成加工时间函数；c（j，k）：任务j∈J 在机器k 上的最早完工时间，s：In↦JN为任务排序函数，s（i）≠s（i′），i≠i′；s（i）表示第i个被加工的任务.

模型（1）表述出了不同任务在不同机器上的开始加工时间，模型（2）是在此基础上加入各自的加工时间所求得其相应的完工时间.模型中的m＋1表示任务完工后的停留区域，x（s（i），m＋1）表示第i个被加工任务完成的时间.这里，任务排序函数s 给出了一种任务的排序方式，s（i）∈J表示第i个被加工的任务，（s（1），s（2），s（3），…，s（n））表示按序加工的任务列.

可以证明，模型（1）存在如下不等式关系

为此若补充定义s（0）≜0，x（0，k）≜ε，x（j，0）≜ε，则模型（1）可简化为如下形式：

通过递推可知：

模型（4）与（5）分别表示出第i个被加工任务在机器m 上的开始加工时间和完工时间，模型中涉及到第i个被加工任务的各时间参数与其前一个被加工任务在各个机器上的开始加工时间，换句话说，第i个被加工任务在第m 台机器上的完工时间，只与其前一个任务调度有关.

2 阻塞流水车间启发式动态规划调度算法

如果考虑完工时间之和最小，阻塞流水车间最优调度可以描述为

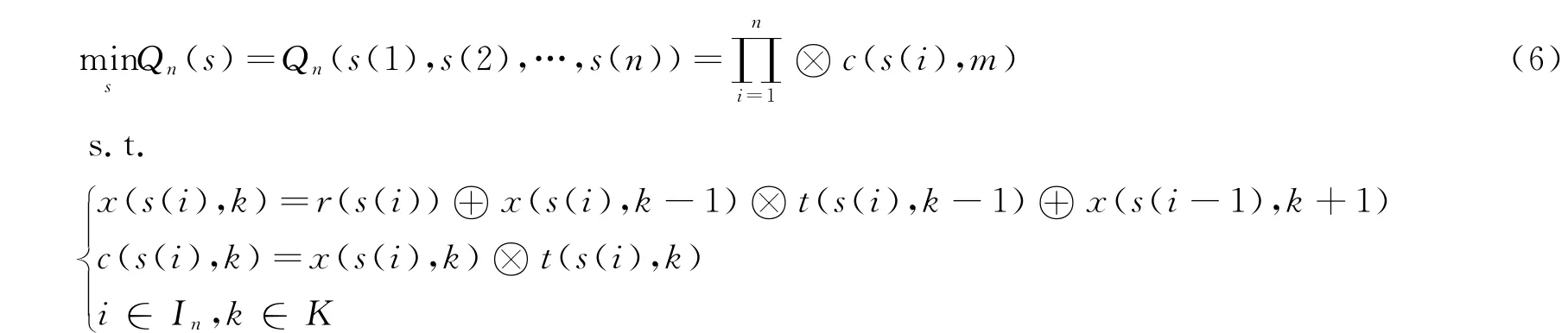
这里简称其为Qn（s）问题.

为便于问题的求解，引入任务集J（i）＝JN／｛s（1），s（2），…，s（i）｝，i∈In.显然有

其中，J（0）＝JN.

定义1 称｛s＊（1），s＊（2），…，s＊（n）｝为Qn（s）问题的一个次优解，如果其满足：

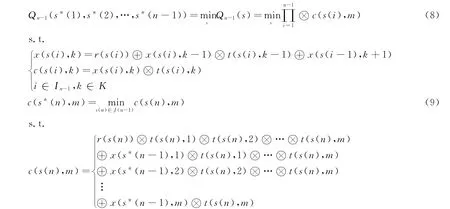
式中，J（n）＝JN／｛s＊（1），s＊（2），…，s＊（n-1）｝.

定义2 称｛s＊（1），s＊（2），…，s＊（n）｝为Qn（s）问题的一个满意解，如果∀i∈In，满足

式中，J（i）＝JN／｛s＊（1），s＊（2），…，s＊（i-1）｝.

基于以上定义，可以给出如下阻塞流水车间启发式动态规划调度算法：

其中，J（0）＝JN，｛s＊（0）｝＝Ø.

3 计算实例分析

为检验算法的有效性，这里给出一个有4个任务4台机器的阻塞流水车间调度问题的例子，表1为各任务在每台机器上的加工时间参数表.表2为启发式动态规划调度算法形成的一组调度计算表，分步骤地将问题中的4个任务进行对比计算，得出任务的优化排序与完工时间之和，表3将表2得出的结果与其他排序得出的结果进行对比，利用启发式动态规划调度算法求出的排序所得的任务完工时间之和为这个值小于表中另外两组排序所得的结果，可见算法十分有效.优化排序后对应的甘特图如图1所示.由甘特图分析可知，任务在各台机器上的加工时间连续，各台机器的空闲时间较短，整条流水线的生产作业比较顺畅，表明阻塞流水车间启发式动态规划调度算法能够求出较好的近优解，算法所得出的结果是比较合理的.

表1 任务的加工时间参数表Table 1 The processing time parameter table of task

表2 启发式动态规划调度表Table 2 The schedule of heuristic dynamic programming

表3 不同排序的对比结果Table 3 The results of different sort

图1 阻塞流水车间调度甘特图Fig.1 Thescheduling Gantt chart of blocking flow shop

4 结 论

本文以阻塞流水车间调度问题为研究背景，以极大代数（dioid）思想为出发点，从另一角度给出了阻塞流水车间的排序函数与调度模型，并用启发式动态规划算法解决了此类问题.实验结果表明，文章采用启发式动态规划算法得到的排序结果优于表3中其他排序的结果.因此，本文所研究的启发式动态规划算法具有较好的可行性.

［1］谢谢，李彦平.带有单服务器的并行机调度问题［J］.沈阳大学学报：自然科学版，2012，24（4）：66-69.（Xie Xie，LI Yanping.Scheduling Parallel Machines with a Single Server［J］.Journal of Shenyang University：Natural Science，2012，24（4）：66-69.）

［2］Celia A G，Hans K.Parallel Machine Scheduling with Job Assignment Restrictions［J］.Naval Research Logistics，2007，54（3）：250-257.

［3］陈露，奚立峰，蔡建国，等.一种求解带有阻塞限制的混合流水车间的禁忌搜索算法［J］.上海交通大学学报，2006，40（5）：856-859.（Chen Lu，Xi Lifeng，Cai Jianguo，et al.A Tabu Search Algorithm for Hybrid Flow Shop Problem with Blocking Constraint［J］.Journal of Shanghai Jiaotong University，2006，40（5）：856-859.）

［4］洪宗友，庞哈利.基于折衷策略的Blocking流水车间调度构造启发式算法［J］.系统工程理论与实践，2008，28（10）：114-118.（Hong Zhongyou，Pang Hali.Study on a Constructive Heuristic Algorithm based on Compromise Policy for Blocking Flow-shop Scheduling［J］.Systems Engineering-Theory ＆Practice，2008，28（10）：114-118.）

［5］洪宗友，闫萍，庞哈利.Blocking流水车间调度问题的MBT算法研究［J］.辽宁师范大学学报：自然科学版，2007，30（2）：148-151.（Hong Zhongyou，Yan Ping，Pang Hali.Study on Minimum Blocked Time Algorithm for Blocking Flow-shop Scheduling［J］.Journal of Liaoning Normal University：Natural Science Edition，2007，30（2）：148-151.）

［6］Pan Q K，Wang L.Effective Heuristics for the Blocking Flow Shop Scheduling Problem with Makespan Minimization ［J］.Omega-International Journal of Management Science，2012，40（2）：218-229.