Dijkstra 最短路径算法的优化及在应急交通中的应用
姜惠娟
(定西师范高等专科学校 计算机系,甘肃 定西 743000)
1 问题的提出
随着城市规模的快速发展,城市交通也越来越复杂,在紧急救援物资运输、医疗急救、110 报警、火警等应急交通中一般要求能在尽可能短的时间内找到到达目标地的最佳路线,而且在行车途中通常需要实时计算车辆前方的路线、路况,这就要求能计算任意两个节点间的最短路径,而且问题的解决是高效的.而传统的Dijkstra 算法解决的是从一定点到其他各节点的最短路径,且计算时间长、所需存储空间大.笔者在分析Dijkstra 算法特征的基础上,从两个方面对算法进行改进.将改进后的算法应用于应急交通系统中搜索最佳路径,实践证明,该方法提高了效率.
我们通常所说的最短路径不仅指距离最短,还可以指时间最短、费用最小、线路容量最小等.相应地,最短路径问题就成为最快路径问题、最低费用等问题,即:最优路径问题实质是求加权图G=<V、E、W >中给定两点间的最短路径,而迪克斯特拉(Dijkstra)算法就是求最短路径的著名算法之一[1].
2 Dijkstra 最短路径算法分析
2.1 算法描述
带权有向图用G=<V,E >表示,其中V 是顶点集,E 是边的集合,该算法的核心是按照路径长度递增的次序产生最短路径.图中的顶点集合V 分成两组,用M 表示已求出最短路径的顶点集合,用N 表示尚未确定最短路径的顶点集合,用数组T[N]表示某步中从vi到vk的最短路径.算法核心步骤可归纳为:
(1)初始时,M={vi},N=V-{vi},如果vi到vk有弧,T[k]等于该弧上的权值;如果无弧存在,则T[k]等于无穷大;
(2)从N 中找T[k]最小的vk加入M,并将其从N 中删除,若N 为空,算法结束,否则进行步骤(3);
(3)将k 结点与N 中其他结点比较,若T[j]>T[k]+arcs[k][j](弧<vj,vk>上的权值),那么用T[k]+arcs[k][j]代替原来的T[j],重复步骤(2);
(4)算法结束,这时T[k]中存放的即为从vi到vj的最短路径.
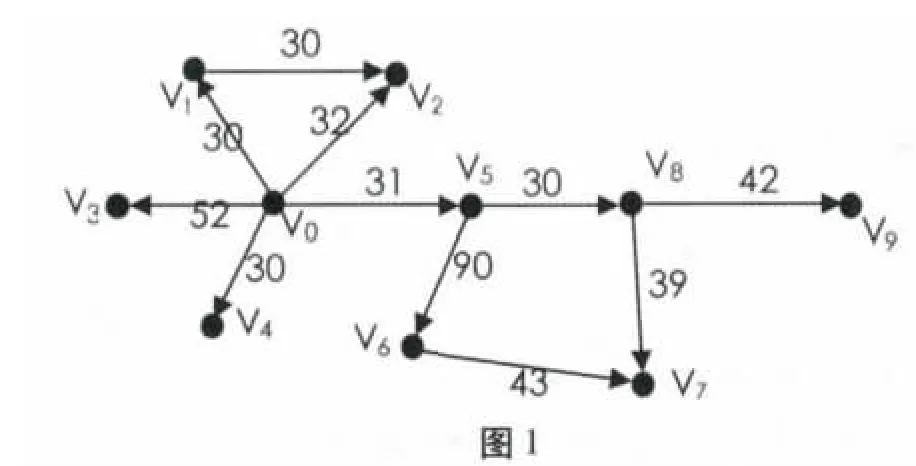
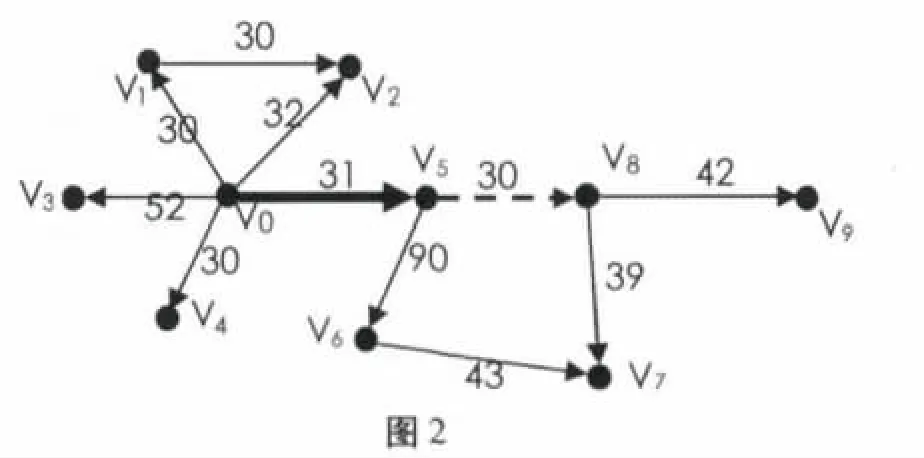
某地区部分交通线路图如图1 所示,采用Dijkstra 算法寻找从v0到v7的最短路径,图2 中加粗部分表示已经找到的最短路径.对于已经找到的每条路径长加上相邻顶点和已知路径中相应顶点间的距离和作比较,选出最接近起点vo的下一条顶点v8,然后将弧<v5,v8>加入到已知的最短路径中,采用同样的方法循环,直到查找到所有的最短路径.
2.2 算法时间效率分析
首先,Dijkstra 算法产生的是一棵以源点v0为根的树,算法执行则该树向四周延伸,其中有些分支对求最短路径是没有帮助的;其次,算法的每次循环就是从待处理的节点集合N 中取距离最小的一个节点加入M 中,使最优路径扩大一个节点,从而保证一步最优,但整体效果并未最优[2].
Dijkstra 算法本身时间复杂度为Ο(n2),如果要求任意两个结点间的最短路径,则需要重复执行Dijkstra 算法n 次[3],所以总的时间复杂度为Ο(n3).当网络节点数n 增大时,计算时间会成倍或幂次增大.因此,在交通线路非常复杂的情况下,该算法运算时间长、求解效率低,很难满足应急交通系统的实际要求.
3 优化Dijkstra 最短路径算法
3.1 根据图节点的出、入度优化算法
3.1.1 根据节点的出度优化算法
优化思想:若结点vi的出度为1,则它只有唯一的后继节点vj,那么vi到vj的最短路径即为弧<vi,vj>上的权值[3];vi到其他各结点的最短路径就等于vj到其他各结点的最短路径加上弧<vi,vj>上的权值即可.
根据以上思想,优化后算法的具体步骤可以总结如下:
(1)计算所有结点的出度;
(2)将出度为1 的结点用si表示;
(3)如果一个节点的出度为1,则不必求从此结点出发的最短路径,先求其后继结点到其他节点的最短路径,在此基础上加上si节点的唯一出度边的权值则可得到从该si节点出发到其他节点的最短路径;
(4)重复步骤(2)、(3),直到没有出度为1 的结点.
如图1 中,结点v1、v6的出度为1,v1的唯一后继结点为v2,v6的唯一后继结点为v7,因此不必先求这两点到其他结点的最短路径,只需先求出v2、v7结点到其他结点的最短路径,v1到其他结点的最短路径即为v2到相应结点的最短路径加上弧<v1,v2>上的权值;v6到其他结点的最短路径即为v7到相应结点的最短路径加上弧<v1,v2>上的权值.
3.1.2 根据节点的入度优化算法
优化思想:如果某结点的入度为0,则其他结点到该结点均不可到达,因此其他节点到该节点的最短路径均为无穷大,而且该节点不会出现在其他任意两个结点间的最短路径上,所以在计算其他各结点间的最短路径时,可以将入度为0 的结点先删除.根据此优化思路,以下是优化后算法的具体步骤:
(1)计算各结点的入度;
(2)将入度为0 的结点用vi表示;
(3)采用Dijkstra 算法计算从vi到其他各结点的最短路径;
(4)求完最短路径后如果结点vi的入度为0,则将该结点从图中删除,以简化有向图,从而简化了后面的计算过程;
(5)重复步骤(2)、(3),直到没有入度为0 的节点.
如图1 所示,v0的入度为0,当计算出以v0结点出发到其他各结点的最短路径后,再计算其他结点间的最短路径时,就可以将结点A 删除,并把其他结点到v0结点的最短路径标为无穷大.
通过算法优化,提前消减了图中无益于求最短路径的分支,提高了效率.
注意,不管是从入度还是从出度优化,都必须考虑出入度为1 的多个结点,而且要注意该节点的前驱结点的次序.
3.2 根据已知的最短路径快速计算其他最短路径
如果R,S,T 是从R 到T 的最短路径,则R 到S 的最短路径、S 到T 的最短路径不必再采用Dijkstra算法去计算,而可以通过已经得到的R 到T 的最短路径直接得到:R 到S 的最短路径为R,S,S 到T 的最短路径为S,T[4].
证明:已知结点R 到结点T 的最短路径为R,S,T;假设结点R 到结点S 的最短路径不是R,S;而是R,…,S;那么可得出R,S,…,T;此路径比路径R,S,T 更短,这与已知条件R 到T 的最短路径为R,S,T相矛盾.于是,得到R 到S 的最短路径一定为R,S;同理可以得到S 到T 的最短路径为S,T.
在图3 中,如果O 到Q 的最短路径已经算出为:O,P,S,Q,则直接可以得出O 到P 的最短路径为:O,P;O 到S 的最短路径为:O,P,S;P 到S 的最短路径为:P,S;P 到Q 的最短路径为:P,S,Q,而不需要再采用Dijkstra 算法去计算.
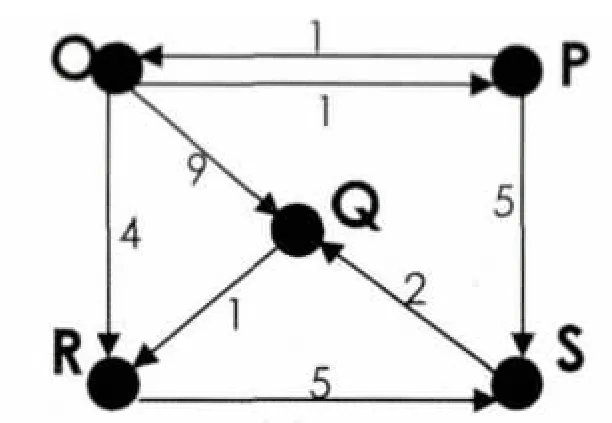
图3
采用此优化策略对图3 中任意两结点快速计算最短路径的具体步骤如下所示:
O 到Q 的最短路径:O,P,S,Q——直接由Dijkstra 算法计算得到;
O 到P 的最短路径:O,P——由已知最短路径直接得到;*
O 到S 的最短路径:O,P,S——由已知最短路径直接得到;*
P 到S 的最短路径:P,S——由已知最短路径直接得到;*
P 到Q 的最短路径:P,S,Q——由已知最短路径直接得到;*
P 到R 的最短路径:P,O,R——直接由Dijkstra 算法计算得到;
P 到O 的最短路径:P,O——由已知最短路径直接得到;*
O 到R 的最短路径:O,R——由已知最短路径直接得到;*
R 到Q 的最短路径:R,S,Q——直接由Dijkstra 算法计算得到;
R 到S 的最短路径:R,S——由已知最短路径直接得到;*
S 到Q 的最短路径:S,Q——由已知最短路径直接得到;*
Q 到S 的最短路径:Q,R,S——直接由Dijkstra 算法计算得到;
Q 到R 的最短路径:Q,R——由已知最短路径直接得到;*
R 到S 的最短路径:R,S——由已知最短路径直接得到;*
S 到R 的最短路径:S,Q,R——直接由Dijkstra 算法计算得到;
S 到Q 的最短路径:S,Q——由已知最短路径直接得到;*
Q 到R 的最短路径:Q,R——由已知最短路径直接得到.*
从优化后的算法可以看出17 组结点间的最短路径,只有末用星号标注的组是直接采用Dijkstra 算法计算到,其他均采用已经得到的最短路径直接得出,最短路径的查找效率提高了许多[5].
4 小结
随着最短路径算法在人们实际生活中的应用越来越广泛,研究高效的最短路径算法很有价值.本文对Dijkstra 经典算法的执行过程分析后,针对该算法存在的计算时间长、效率低等问题,从节点的出、入度信息和全局最优化两个角度对Dijkstra 算法进行优化,给出了算法的实现过程.实践证明,将优化后的算法应用于应急交通系统中有效地减少了最短路径的计算时间,提高了查找效率.
[1]严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,2007.
[2]邓春燕.两种最短路径算法比较[J].电脑知识与技术,2008,15(12):511-513.
[3]田丰.图与网络流理论[M].北京:科学出版社,1987.
[4]龙光正,杨建军.改进的最短路算法[J].系统工程与电子技术,2009,24(6):106-108.
[5]土晓东,陈国龙,林柏钢.网络最短路问题的改进算法[J].小型微型计算机系统,2009,23(9):1083-1087.

